B样条基函数的定义：

$\begin{aligned} &N_{i, 0}(u)=\left\{\begin{array}{ll} {1} & {\text { if } u_{i} \leq u<u_{i+1}} \\ {0} & {\text { otherwise }} \end{array}\right.\\ &N_{i, p}(u)=\frac{u-u_{i}}{u_{i+p}-u_{i}} N_{i, p-1}(u)+\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+1}} N_{i+1, p-1}(u) \end{aligned}$

沿着下图所示的三角形进行计算：

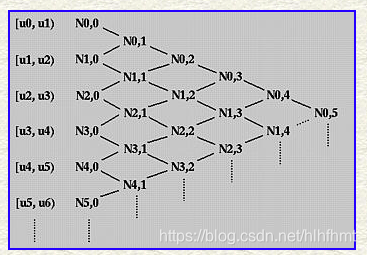
这是关于B样条基函数的第一个重要的三角形，可以确定基函数的非零节点区间：

B样条基函数Ni_j(u)的非零节点区间为[u(i),u(i+j+1)),0=<j<=k

显然上式计算是递归形式的，MATLAB函数支持递归，函数定义如下：

function Bf = getBaseFunVal(u,i,k,U)
% 计算基函数Ni_k(u)

Val = 0;
val1 = 0; val2 = 0;

if (k == 0)
    if u>=U(i +1)&&u<U(i+1 +1)  % u<U(i +1)||u>=U(i+1 +1)
        Val = 1;
        Bf = Val;
        
    else
        Bf = Val;
    end
end

if (k>0)
    if  u<U(i +1)||u>=U(i+k+1 +1)
        Bf = Val;
    else
        alpha = 0;
        beta = 0;
        dTemp = 0;
        
        dTemp = U(i+k +1) - U(i+ 1);
        if dTemp == 0
            alpha = 0;        % 0/0 = 0
        else
            alpha = (u - U(i+ 1))/dTemp;
        end
        
        dTemp = U(i+k+1 +1) - U(i+1 +1);
        if dTemp == 0
            beta = 0;           % 0/0 = 0
        else
            beta = (U(i+k+1 +1) - u)/dTemp;
        end
        
        val1 = alpha*getBaseFunVal(u,i,k-1,U);  % 第一项递归
        val2 = beta*getBaseFunVal(u,i+1,k-1,U); % 第二项递归
        Val = val1 + val2;
        Bf = Val;
    end
end

end

现在利用上面的函数计算非零基函数N3_2(u)，并绘图：

clear,clc,close all;
% 计算节点区间内非零基函数的值
%-------------------------------------------------------------
% test:
k = 2;
U = [0 0 0 1 2 3 4 4 5 5 5];
n = length(U) - k -1;

B = [];
for j = 1:0.001:4
    bj = getBaseFunVal(j,3,k,U);
    B = [B;bj];
end
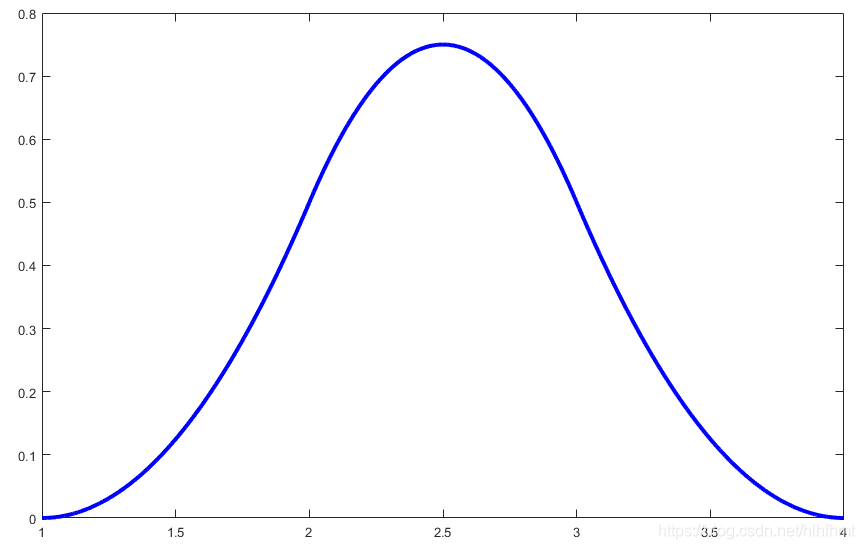
plot(1:0.001:4,B,'b','linewidth',3);

N3_2(u)为[定义在节点区间u(3), u(6))=[1, 4)上的分段二次多项式曲线：

参考文献：

施法中. 计算机辅助几何设计与非均匀有理B样条[M]. 2001.

原文链接：https://blog.csdn.net/hlhfhmt/article/details/103770988