递归与回溯

一、递归 (Recursive)

我们在路上走着，前面是一个多岔路口，因为我们并不知道应该走哪条路，所以我们需要尝试。尝试的过程就是一个函数。

我们选择了一个方向，后来发现又有一个多岔路口，这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上，再做一次尝试，即在函数内部再调用一次函数，这就是递归的过程。

二、回溯 (Backtrack)

这样重复了若干次之后，发现这次选择的这条路走不通，这时候我们知道我们上一个路口选错了，所以我们要回到上一个路口重新选择其他路，这就是回溯的思想。

回溯的思路基本如下：当前局面下，我们有若干种选择，所以我们对每一种选择进行尝试。如果发现某种选择违反了某些限定条件，此时 return；如果尝试某种选择到了最后，发现该选择是正确解，那么就将其加入到解集中。

在这种思想下，我们需要清晰的找出三个要素：选择 (Options)，限制 (Restraints)，结束条件 (Termination)。

eg. LeetCode - 22 括号生成

递归：就是函数的一次次可能性的罗列
回溯：就是用if else语句给了多个限制条件

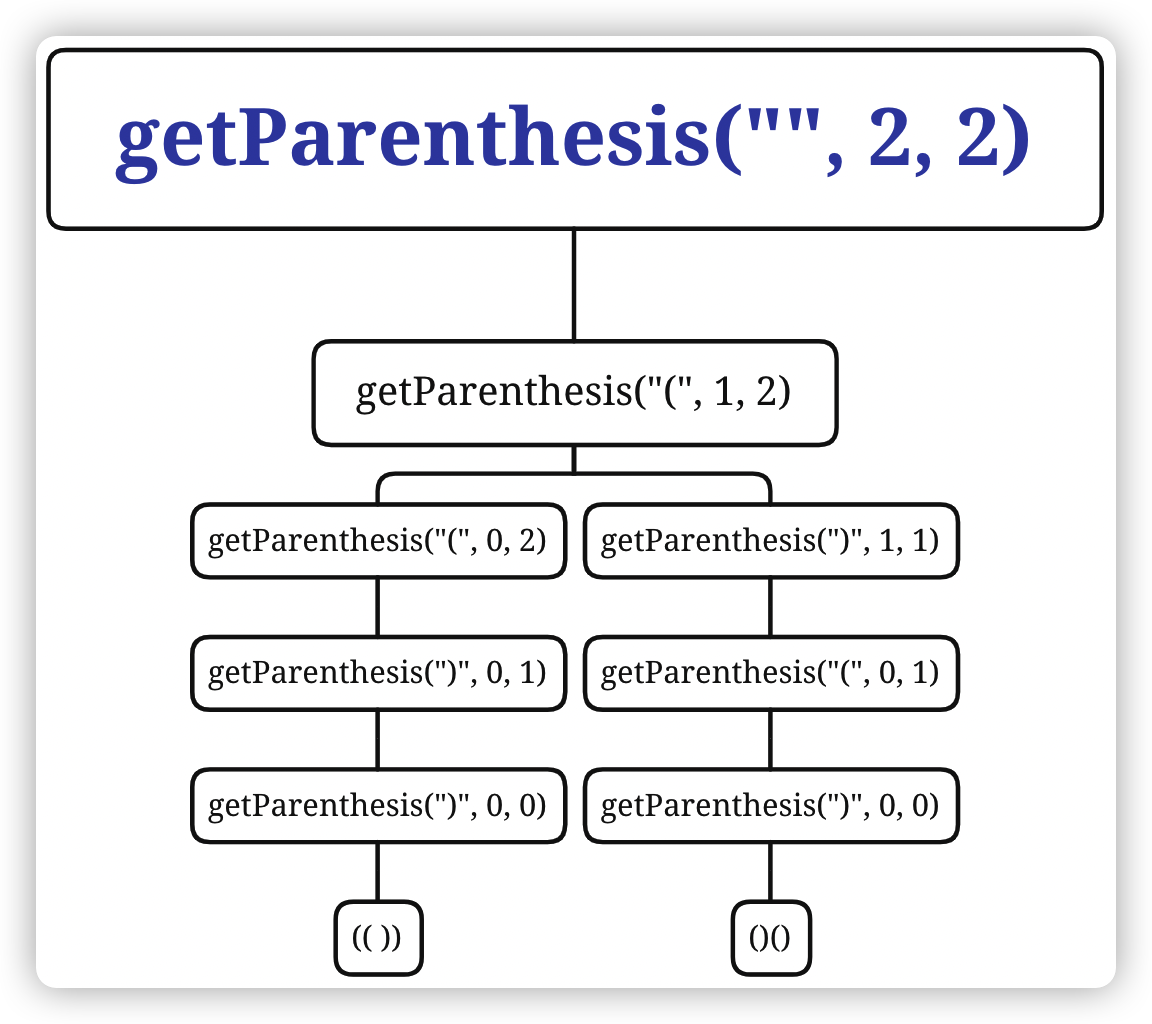
箭头表示函数中调用函数
从左向右越来越深

class Solution {
    List<String> res = new ArrayList<String>();
    
    public List<String> generateParenthesis(int n) {
        if (n <= 0){
            return res;
        }
        getParenthesis("", n, n);
        return res;
    }

    public void getParenthesis(String str, int left, int right){
        // 递归出口
        if (left == 0 && right == 0){
            res.add(str);
            return;
        } 
        if (left == right){
            //剩余左右括号数相等，下一个只能用左括号
            getParenthesis(str+"(", left-1, right);

        } else if (left < right){
            //剩余左括号小于右括号，下一个可以用左括号也可以用右括号
            if (left > 0){
                getParenthesis(str+"(", left-1, right);
            }
            getParenthesis(str+")", left, right-1);
        }
    }
}