1. 概述
一般商用的数字下变频抽取滤波器(DDC)方案中,采用CIC抽取滤波器作为第一级(一般采用5级以下的CIC级联),每一级DDC基本上能提供13.3dB左右的衰减。也就是说,5级CIC级联滤波器最多能提供65dB左右的阻带衰减。但如果设计的DDC要求衰减达到100dB以上,就要求实现的CIC至少达到8级级联,这并不常见,设计的时候需要考虑多种问题。而且而CIC之后需要加上补偿滤波器,否则CIC滤波之后的通带不平坦(超过0.5dB,甚至超过1dB,一般的设计要求在0.01dB之内),通带内衰减严重。
2. CIC数字抽取滤波器结构
a. 单级CIC滤波器
CIC滤波器包括两个基本结构:积分结构和梳状结构。对应的CIC抽取滤波器和CIC插值滤波器分别如下:(懒,直接截图了~)
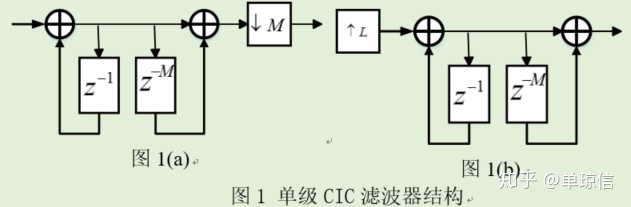

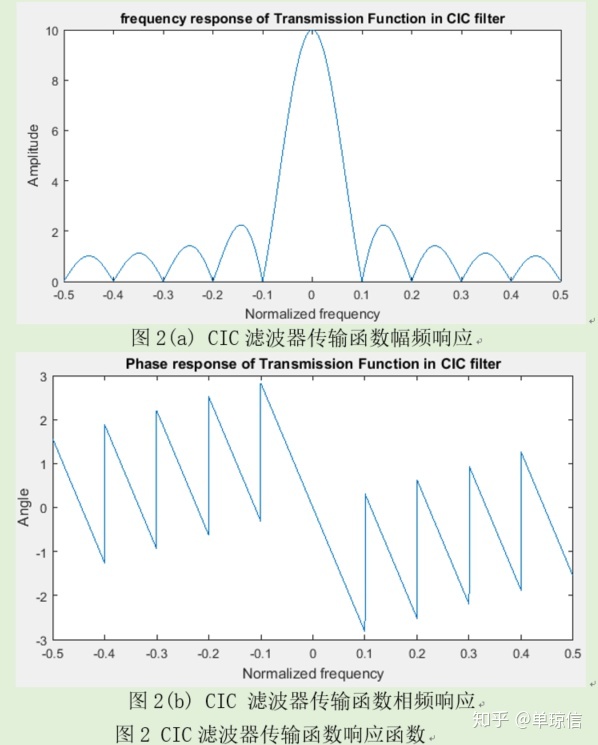
分析公式(6)可知,虽然CIC滤波器的极点在单位圆上,但是滤波器的系数都是1,故在采用硬件实现CIC滤波器时,即使是采用定点精度,也不存在量化误差。而且即使存在递归项,其传输函数的相频响应依然是线性的,故即使使用有限精度的数来表示,CIC滤波器依然可以做到稳定。这一性质在硬件实现中是极为重要的。
由图2.1(a)可见,随着频率的增大,旁瓣电平不断减小,当D>>1时,第一旁瓣的电平为 ,它与主瓣电平的差值为13.46dB。由此可见,单级CIC滤波器的旁瓣电平较大,阻带衰减较差。为了降低第一旁瓣峰值电平,可以采用级联型的多级CIC滤波器实现。
(2) 多级CIC滤波器
假设采用的多级CIC滤波器的级数为N,则其阻带衰减为单级CIC滤波器的N倍,即是 (dB)。以抽取滤波器为例,其传输函数的近似如下:
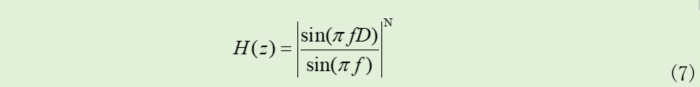
当然,在提高阻带衰减性能的同时,带来的是硬件消耗资源的增大,由于CIC滤波器通常需要工作在全精度数值中,这样就使数值的位宽增加到Mlog2(D),这就意味着在多级的CIC滤波器中,会有大量位宽较大的数据使用。然而这样也不妨碍其大量商用。CIC滤波器主要用于速率转换模块中,CIC抽取滤波器和CIC插值滤波器的结构示意图如下图:

上面的图示中,CIC工作在非常高的速率中,可以采用Noble变换的等效CIC抽取滤波器结构。经过Noble变换的结构最容易实现且占用最少的资源。这种简单有效的CIC抽取滤波器称为Hogenauer抽取滤波器。以下首先对Noble变换恒等式进行介绍。
(3) Noble恒等式
当多级系统包括线性系统、抽取滤波器和内插滤波器时,可以下信号处理的流程中重新排列这3部分的处理顺序,以便系统可以以更加简单的形式出现。这就是Noble恒等式的主要思想。Noble恒等式变换结构如下图。
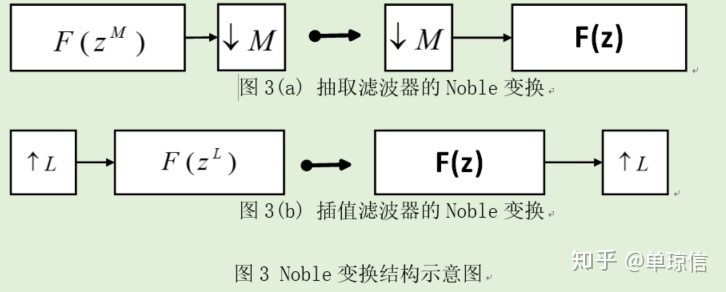
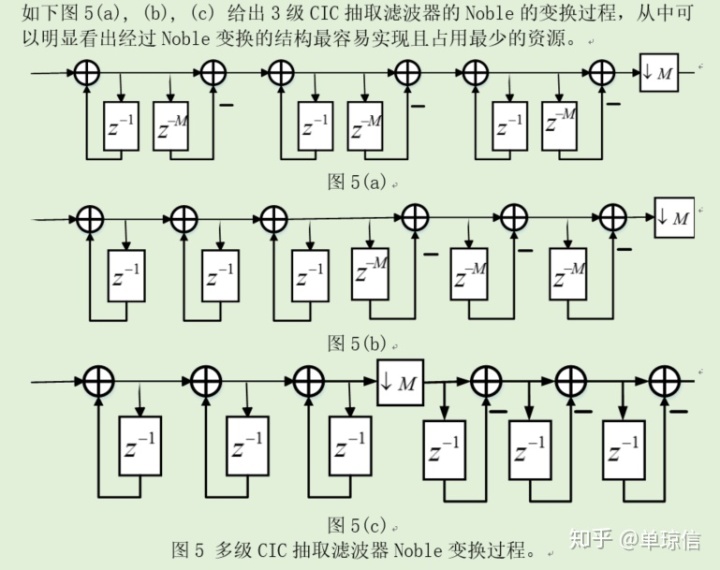
如果线性系统后面紧跟着抽取滤波器,如上图4(a)所示,则有如下等式:
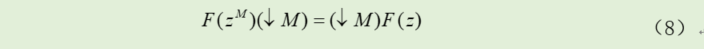
(4) 多级CIC抽取滤波器
3. 补偿滤波器
CIC滤波器带来的另外一个问题就是回导致通带的弯曲下垂,而且级联越多级,问题越严重。这样导致通带变窄和过渡带变宽等问题。在典型的抽取或插值滤波器应用,需要一个比较合理的平坦的通带和较窄的过渡带。而多级CIC滤波器本身不满足这样的需求,这就需要在CIC滤波器后面级联一个额外的补偿滤波器。对于CIC抽取滤波器来说,通常级联一个非递归FIR滤波器进行补偿。
4. 多级CIC滤波器结构设计
(1)积分(累加)溢出分析
每一级CIC滤波都是由积分器和梳妆滤波器组成,积分器实质上就是累加器,累加过程则会存在溢出情况,但是如果累加器位宽足够宽且CIC滤波器采用二进制补码形式,那么不管积分器是否发生内部溢出,CIC滤波器的输出结果都是正确的。累加器的位宽足够宽是指,累加器的宽度必须为输入比特数和用于表示CIC M抽头原型滤波器的增益M所需的比特数之和。累加的比特宽度如下:
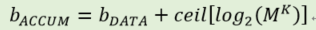
其中,是输入信号的位宽,是累加过程所需位宽,K是CIC的级联数,M是梳妆滤波器长度(即抽取倍数)。假设用一个抽取倍数为16,级联为8级的CIC滤波器对18比特的输入数据进行处理,则可以得到累加位宽为18+32 = 50。
(2)通带要求
观察CIC滤波器的频率响应曲线可知,滤波器主瓣响应中与频率有关的增益在减小。这种非均匀通带增益将是滤波器要处理的基带频谱发生畸变。主瓣增益衰减通常会限制输入信号带宽必须小于主瓣带宽的25%,假设下变频倍数为M,即抽头延迟单位,则对应的通带带宽要求小于1/(4M)。
(3)削减累加器宽度
为了从内部累加器溢出中得以成功恢复,CIC滤波器中发生了比特增长现象。该比特增长反映了滤波器输入输出之间的滤波增益。在增采样滤波器中,连续的各级积分器上会发生比特增长现象,积分器链上开始端和结束端的积分器所需要的比特宽度不同。可以通过将累加器中最重要的比特削减掉,来达到与各积分器最大增益相适应的水平。在减采样器中,第一级积分就出现比特增长现象,而且所有的后续积分器和梳妆滤波器都必须保留第一级积分器的重要特性。
参考文献[1][2]可以得到可以丢弃的LSB如下推导:

上述所说的cic.exe文件是Digital Signal Processing with Field Programmable Gate Arrays这本书的附带中在util中一个可执行文件。实际根据上述推导算法可以自己完成matlab代码编写,如下:
% clear
close all
% clc
%% input parameter
Bin = input('input BitWidth: ');
Bout = input('output BitWidth: ');
N = input('number of stages(or sections): ');
D = input('Comb Delay: ');
M = input('Decimation Rate: ');
%% F_j calculation
% 1:N
for j = N:-1:1
h_j = [];
h_j((M*D-1)*N + j -1 + 1) = 0;
for k = 0:(M*D-1)*N + j -1
for L = 0:floor(k/(M*D)) % L 比较容易区分
Change_to_Result = (-1)^L*nchoosek(N, L)*nchoosek(N-j+k-M*D*L,k-M*D*L);
h_j(k+1) = h_j(k+1) + Change_to_Result;
end
end
F_j(j) = sqrt(sum(h_j.^2));
end
% N+1 : 2N
for j = 2*N:-1:N+1
h_j = [];
h_j((M*D-1)*N + j -1 + 1) = 0;
for k = 0:2*N+1-j
h_j(k+1) = h_j(k+1) + (-1)^k*nchoosek(2*N+1-j,k);
end
F_j(j) = sqrt(sum(h_j.^2));
end
% Final output register truncation
F_j(2*N+1) = 1;
Minus_log2_of_F_j = -log2(F_j)';
%% Compute total "Output_Truncation_Noise_Variance" terms
Gain_max = (D*M)^N;
Num_of_Bits_Growth = ceil(log2(Gain_max));
% Num_Output_Bits_With_No_Truncation = Num_of_Bits_Growth +Bin -1;
Num_Output_Bits_With_No_Truncation = Num_of_Bits_Growth +Bin;
Num_of_Output_Bits_Truncated = Num_Output_Bits_With_No_Truncation - Bout;
Output_Truncation_Noise_Variance = (2^Num_of_Output_Bits_Truncated)^2/12;
Output_Truncation_Noise_Standard_Deviation = sqrt(Output_Truncation_Noise_Variance);
Log_base2_of_Output_Truncation_Noise_Standard_Deviation = log2(Output_Truncation_Noise_Standard_Deviation);
%% Compute column vector of "half log base 2 of 6/N" terms
Half_Log_Base2_of_6_over_N = 0.5*log2(6/N);
B_j = floor( Minus_log2_of_F_j +...
Log_base2_of_Output_Truncation_Noise_Standard_Deviation + ...
Half_Log_Base2_of_6_over_N );
%% Create and display "Results" matrix
disp(['Num of Bits Growth Due To CIC Filter Gain = ', num2str(Num_of_Bits_Growth)])
disp(['Num of Accumulator Bits With No Truncation = ', num2str(Num_Output_Bits_With_No_Truncation)])
disp('bit to cut: ');
disp(transpose(B_j));
Results = zeros(2*N+1,5);
for Stage = 1:2*N
Results(Stage,1) = Stage;
Results(Stage,2) = F_j(Stage);
Results(Stage,3) = Minus_log2_of_F_j(Stage);
Results(Stage,4) = B_j(Stage);
Results(Stage,5) = Num_Output_Bits_With_No_Truncation - B_j(Stage);
end
% Include final output stage truncation in "Results" matrix
Results(2*N+1,1) = 2*N+1; % Output stage number
Results(2*N+1,2) = 1;
Results(2*N+1,4) = Num_of_Output_Bits_Truncated;
Results(2*N+1,5) = Bout;
%Results % Display "Results" matrix in raw float-pt.form
disp(' ')
disp(' Stage(j) Bj Accum (adder) width')
for Stage = 1:2*N
disp([' ',sprintf('%d',Results(Stage,1)), sprintf('t'),...
sprintf('%5.5g',Results(Stage,4)),sprintf('t'),...
sprintf('%7.5g',Results(Stage,5))])
end
disp([' ',sprintf('%d',Results(2*N+1,1)),...
sprintf('t'),...
sprintf('%5.5g',Results(2*N+1,4)),sprintf('t'),...
sprintf('%7.5g',Results(2*N+1,5)),' (final truncation)'])
5. 设计过程
现假设设计一个阻带增益至少100dB(对应需要8级CIC)或者110dB(对应需要9级CIC),通带纹波小于0.01dB的抽取滤波器。
(1)CIC滤波器设计
CIC滤波器的设计可以采用MATLAB的fdatool进行设计,但首先需要根据截位算法算出各级CIC滤波器中的LSB截位。如果采用cic.exe,打开,其界面如下:
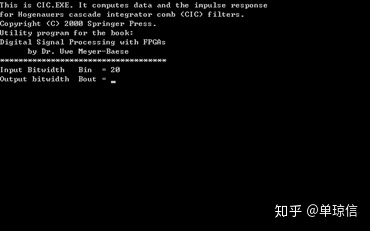
输入对应的参数,得到对应的结果,如下:
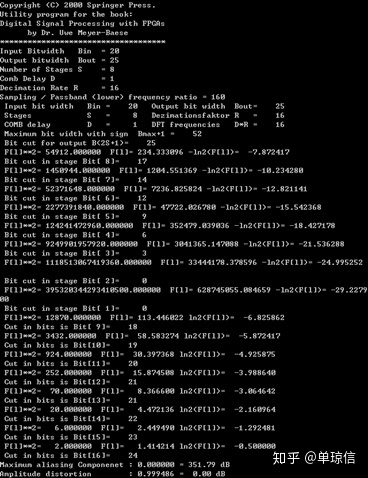
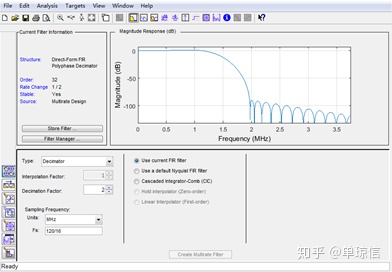
得到16个被截位掉的LSB依次为:0,0,3,6,9,12,14,17,18,19,20,21,21,22,23, 24。最高位为52。对应的fdatool设计如下:
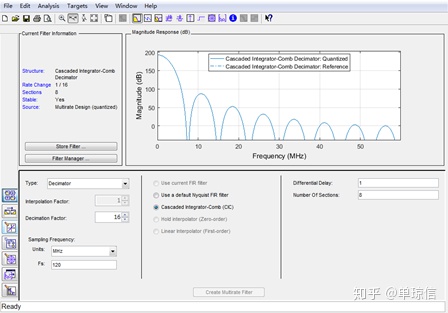
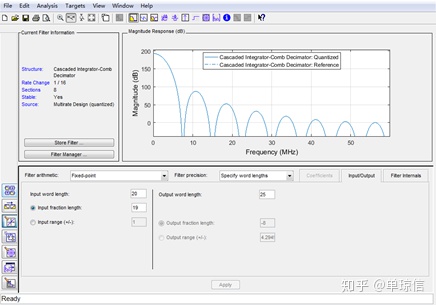
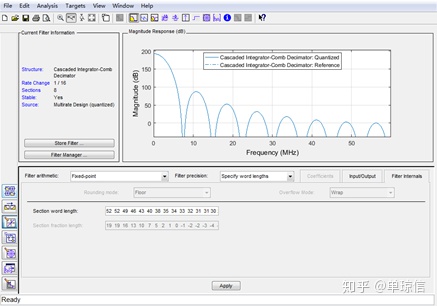
(2)补偿滤波器设计
补偿滤波器也可以采用fdatool进行设计,采用反sinc函数进行设计,设计的参数界面如下:
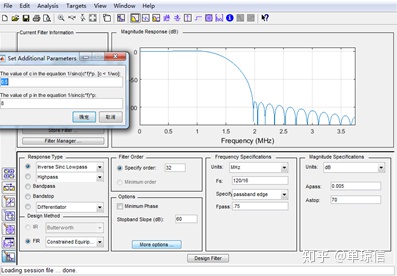
这里需要主要的是,在More options中的参数很重要,与CIC滤波器的阶数相对应的,调节CFIR的Astop来调整CIC旁瓣值。More options里边的第一个参数c的设计跟CIC设计里边的differential Delay对应上,differential Delay如果是1的话,c设计为0.5(可以从0.49~0.51作调节,根据通带的宽度作稍微调0.495~0.5节),如果differential Delay是2,则c为1(可以从0.99~1.1作调节,根据通带的宽度作稍微调节0.995~1.0),另外c越大,校正度越过,因此需要稍微调试实验。More Options里边的第二个参数对应CIC滤波器设计中的Number of Sections,两个参数的值是一致的。
PS:
如果想采用FPGA进行简单实现,可以使用MATLAB fdatool中的HDL代码实现功能直接生成verilog或者VHDL代码,可以参考研习。
6. 参考文献
[1] An Economical Class of Digital Filters for Decimation and Interpolation.
[2] Digital Signal Processing with Field Programmable Gate Arrays.