灰度图像和彩色图像的直方图均衡化(python实现)
原理描述
直方图均衡化
直方图是图像中像素强度分布的图形表达方式。它统计了每一个强度值所具有的像素个数。直方图均衡化是通过拉伸像素强度分布范围来增强图像对比度的一种方法。是图像处理领域中利用图像直方图对对比度进行调整的方法。均衡化指的是把一个分布(给定的直方图)映射到另一个分布(一个更宽更统一的强度值分布),所以强度值分布会在整个范围内展开。映射函数应该是一个累积分布函数。直方图均衡化是通过调整图像的灰阶分布,使得在0~255灰阶上的分布更加均衡,提高了图像的对比度,达到改善图像主观视觉效果的目的。对比度较低的图像适合使用直方图均衡化方法来增强图像细节。这种方法通常用来增加许多图像的全局对比度,尤其是当图像的有用数据的对比度相当接近的时候。通过这种方法,亮度可以更好地在直方图上分布。这样就可以用于增强局部的对比度而不影响整体的对比度,直方图均衡化通过有效地扩展常用的亮度来实现这种功能。这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景噪声的对比度并且降低有用信号的对比度。
直方图均衡化算法
- 统计原始图像各灰度级的像素数目ni,0≤i<L, L是图像中所有的灰度数(通常为256);
- 图像中灰度为i的像素的出现概率是:px(i)=p(x=i)=ni/n,n是图像中所有的像素数,px(i)实际上是像素值为i的图像的直方图,归一化到[0, 1];
- px的累积分布函数,是图像的累计归一化直方图:
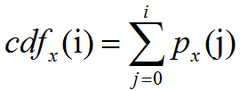
- 直方图均衡化计算公式, cdfmin为累积分布函数最小值,M和N分别代表了图像的长宽像素个数,而L则是灰度级数(如图像为8位深度,则灰度级别共有2^8=256级数,这也是最常见的灰度级数),v为原始图像中为v的像素值:
- 增加了支持甘特图的mermaid语法[^1] 功能;
彩色图像
彩色图像直方图均衡化:上面描述了灰度图像上使用直方图均衡化的方法,但是通过将这种方法分别用于图像RGB颜色值的红色、绿色和蓝色分量,从而也可以对彩色图像进行处理。实际上,对彩色分量rgb分别做均衡化,会产生奇异的点,图像不和谐。一般采用的是用yuv空间进行亮度的均衡即可。本实验我们采用的是将图像由RGB色彩空间到HSI的变换,然后在亮度通道上进行直方图均衡化;均衡化原理同灰度图像。
HSI模型<->RGB模型
HSI颜色模型是一个满足计算机数字化颜色管理需要的高度抽象模拟的数学模型。HSI模型是从人的视觉系统出发,直接使用颜色三要素–色调(Hue)、饱和度(Saturation)和亮度(Intensity,有时也翻译作密度或灰度)来描述颜色。
RGB向HSI模型的转换是由一个基于笛卡尔直角坐标系的单位立方体向基于圆柱极坐标的双锥体的转换。基本要求是将RGB中的亮度因素分离,通常将色调和饱和度统称为色度,用来表示颜色的类别与深浅程度。在图中圆锥中间的横截面圆就是色度圆,而圆锥向上或向下延伸的便是亮度分量的表示。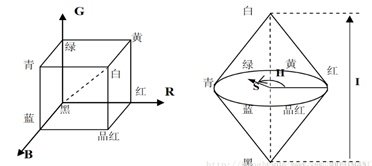
从RGB空间到HSI空间的转换有多种方法,这里仅说明最为经典的几何推导法。RGB转化成HSI的公式为: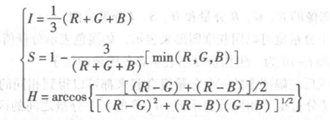
HSI转化成RGB的公式为:

代码
灰度图像直方图均衡化
import cv2
import numpy as np
import matplotlib.pyplot as plt
import collections
# 计算灰度图的直方图
def draw_histogram(grayscale):
gray_key = []
gray_count = []
gray_result = []
histogram_gray = list(grayscale.ravel()) # 将多维数组转换成一维数组
gray = dict(collections.Counter(histogram_gray)) # 统计图像中每个灰度级出现的次数
gray = sorted(gray.items(), key=lambda item: item[0]) # 根据灰度级大小排序
for element in gray:
key = list(element)[0]
count = list(element)[1]
gray_key.append(key)
gray_count.append(count)
for i in range(0, 256):
if i in gray_key:
num = gray_key.index(i)
gray_result.append(gray_count[num])
else:
gray_result.append(0)
gray_result = np.array(gray_result)
return gray_result
def histogram_equalization(histogram_e, lut_e, image_e):
sum_temp = 0
cf = []
for i in histogram_e:
sum_temp += i
cf.append(sum_temp)
for i, v in enumerate(lut_e):
lut_e[i] = int(255.0 * (cf[i] / sum_temp) + 0.5)
equalization_result = lut_e[image_e]
return equalization_result
x = []
for i in range(0, 256): # 横坐标
x.append(i)
image = cv2.imread(r'.\Images\grey.png', cv2.COLOR_BGR2GRAY) # 读取图像
histogram = draw_histogram(image) # 直方图转化
plt.bar(x, histogram) # 绘制原图直方图
plt.savefig('./equalization_gray/before_histogram.png')
plt.show()
lut = np.zeros(256, dtype=image.dtype) # 创建空的查找表,返回image类型的用0填充的数组;
result = histogram_equalization(histogram, lut, image) # 均衡化处理
cv2.imwrite('./equalization_gray/his_grey.png', result) # 保存均衡化后图片
image_equ = cv2.imread(r'.\equalization_gray\his_grey.png', cv2.COLOR_BGR2GRAY) # 读取图像
histogram_equ = draw_histogram(image_equ) # 直方图转化
plt.bar(x, histogram_equ) # 绘制处理后图像直方图
plt.savefig('./equalization_gray/after_histogram.png')
plt.show()
plt.plot(x, lut) # 绘制灰度级变换曲线图
plt.savefig('./equalization_gray/Grayscale_transformation_curve.png')
plt.show()
cv2.imshow('former', image)
cv2.imshow("histogram_equalization", result)
cv2.waitKey(0)
cv2.destroyAllWindows()
彩色图像直方图均衡化(内含hsi模型和rgb模型互换)
import cv2
import numpy as np
import matplotlib.pyplot as plt
import collections
def rgb_hsi(rgb_image):
# 保存原始图像的行列数
rows = int(rgb_image.shape[0])
cols = int(rgb_image.shape[1])
# 图像复制
hsi_image = rgb_image.copy()
# 通道拆分
b = rgb_image[:, :, 0]
g = rgb_image[:, :, 1]
r = rgb_image[:, :, 2]
# 归一化到[0,1]
b = b / 255.0
g = g / 255.0
r = r / 255.0
for i in range(rows):
for j in range(cols):
num = 0.5 * ((r[i, j]-g[i, j])+(r[i, j]-b[i, j]))
den = np.sqrt((r[i, j]-g[i, j])**2+(r[i, j]-b[i, j])*(g[i, j]-b[i, j]))
if den == 0:
hsi_h = 0
else:
theta = float(np.arccos(num / den))
if b[i, j] <= g[i, j]:
hsi_h = theta
else:
hsi_h = 2*np.pi - theta
min_RGB = min(min(b[i, j], g[i, j]), r[i, j])
sum = b[i, j]+g[i, j]+r[i, j]
if sum == 0:
hsi_s = 0
else:
hsi_s = 1 - 3*min_RGB/sum
hsi_h = hsi_h/(2*np.pi)
hsi_i = sum/3.0
# 输出HSI图像,扩充到255以方便显示,一般H分量在[0,2pi]之间,S和I在[0,1]之间
hsi_image[i, j, 0] = hsi_h*255
hsi_image[i, j, 1] = hsi_s*255
hsi_image[i, j, 2] = hsi_i*255
return hsi_image
def hsi_rgb(hsi_image):
# 保存原始图像的行列数
rows = np.shape(hsi_image)[0]
cols = np.shape(hsi_image)[1]
# 对原始图像进行复制
rgb_image = hsi_image.copy()
# 对图像进行通道拆分
hsi_h = hsi_image[:, :, 0]
hsi_s = hsi_image[:, :, 1]
hsi_i = hsi_image[:, :, 2]
# 把通道归一化到[0,1]
hsi_h = hsi_h / 255.0
hsi_s = hsi_s / 255.0
hsi_i = hsi_i / 255.0
B, G, R = hsi_h, hsi_s, hsi_i
for i in range(rows):
for j in range(cols):
hsi_h[i, j] *= 360
if 0 <= hsi_h[i, j] < 120:
B = hsi_i[i, j] * (1 - hsi_s[i, j])
R = hsi_i[i, j] * (1 + (hsi_s[i, j] * np.cos(hsi_h[i, j] * np.pi / 180)) / np.cos(
(60 - hsi_h[i, j]) * np.pi / 180))
G = 3 * hsi_i[i, j] - (R + B)
elif 120 <= hsi_h[i, j] < 240:
hsi_h[i, j] = hsi_h[i, j] - 120
R = hsi_i[i, j] * (1 - hsi_s[i, j])
G = hsi_i[i, j] * (1 + (hsi_s[i, j] * np.cos(hsi_h[i, j] * np.pi / 180)) / np.cos(
(60 - hsi_h[i, j]) * np.pi / 180))
B = 3 * hsi_i[i, j] - (R + G)
elif 240 <= hsi_h[i, j] <= 300:
hsi_h[i, j] = hsi_h[i, j] - 240
G = hsi_i[i, j] * (1 - hsi_s[i, j])
B = hsi_i[i, j] * (1 + (hsi_s[i, j] * np.cos(hsi_h[i, j] * np.pi / 180)) / np.cos(
(60 - hsi_h[i, j]) * np.pi / 180))
R = 3 * hsi_i[i, j] - (G + B)
rgb_image[i, j, 0] = B * 255
rgb_image[i, j, 1] = G * 255
rgb_image[i, j, 2] = R * 255
return rgb_image
# 计算灰度图的直方图
def draw_histogram(grayscale):
# 对图像进行通道拆分
hsi_i = grayscale[:, :, 2]
color_key = []
color_count = []
color_result = []
histogram_color = list(hsi_i.ravel()) # 将多维数组转换成一维数组
color = dict(collections.Counter(histogram_color)) # 统计图像中每个亮度级出现的次数
color = sorted(color.items(), key=lambda item: item[0]) # 根据亮度级大小排序
for element in color:
key = list(element)[0]
count = list(element)[1]
color_key.append(key)
color_count.append(count)
for i in range(0, 256):
if i in color_key:
num = color_key.index(i)
color_result.append(color_count[num])
else:
color_result.append(0)
color_result = np.array(color_result)
return color_result
def histogram_equalization(histogram_e, lut_e, image_e):
sum_temp = 0
cf = []
for i in histogram_e:
sum_temp += i
cf.append(sum_temp)
for i, v in enumerate(lut_e):
lut_e[i] = int(255.0 * (cf[i] / sum_temp) + 0.5)
equalization_result = lut_e[image_e]
return equalization_result
x = []
for i in range(0, 256): # 横坐标
x.append(i)
# 原图及其直方图
rgb_image = cv2.imread(".\Images\color.jpg")
cv2.imshow('rgb', rgb_image)
histogram = draw_histogram(rgb_image)
plt.bar(x, histogram) # 绘制原图直方图
plt.savefig('./equalization_color/before_histogram.png')
plt.show()
# rgb转hsi
hsi_image = rgb_hsi(rgb_image)
cv2.imshow('hsi_image', hsi_image)
cv2.imwrite('./equalization_color/hsi_result.png', hsi_image)
# hsi在亮度分量上均衡化
histogram_1 = draw_histogram(hsi_image)
lut = np.zeros(256, dtype=hsi_image.dtype) # 创建空的查找表
result = histogram_equalization(histogram_1, lut, hsi_image) # 均衡化处理
cv2.imshow('his_color_image', result)
cv2.imwrite('./equalization_color/his_color.png', result) # 保存均衡化后图片
# hsi转rgb
image_equ = cv2.imread(r'.\equalization_color\his_color.png') # 读取图像
rgb_result = hsi_rgb(image_equ)
cv2.imshow('rgb_image', rgb_result)
cv2.imwrite('./equalization_color/gbr_result.png', rgb_result)
rgb = cv2.imread(".\equalization_color\gbr_result.png")
histogram_2 = draw_histogram(rgb)
plt.bar(x, histogram_2)
plt.savefig('./equalization_color/after_histogram.png')
plt.show()
plt.plot(x, lut) # 绘制灰度级变换曲线图
plt.savefig('./equalization_color/Grayscale_transformation_curve.png')
plt.show()
cv2.waitKey(0)
cv2.destroyAllWindows()
实验结果
描述:原灰度图像通过opencv读取到程序中,统计各个灰度级的比重后,按照直方图均衡化的步骤依次计算,得出映射关系,画出直方图及灰度变换曲线图。
原灰度图像及其直方图
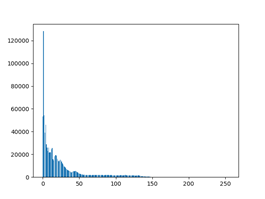
均衡化结果及其直方图
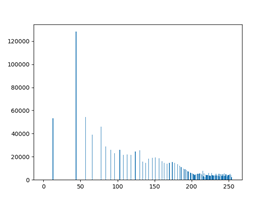
描述:原彩色图像通过opencv读取到程序中,先转换成HSI彩色模型,对I分量即亮度通道进行直方图均衡化,再将均衡化后的图像转换成RGB彩色模型,得出映射关系,画出直方图及灰度变换曲线图。
原彩色图像及其直方图
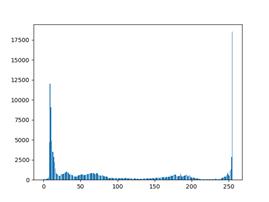
rgb模型转hsi模型图像及其均衡化结果

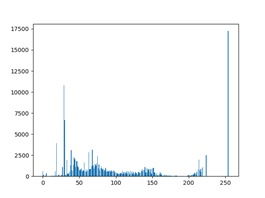
hsi均衡化结果转回rgb图像及其直方图
问题
问题:opencv无法安装
解决方法:python3.8版本与opencv不兼容,改用python3.7即可
问题:重写cv2.split()拆分通道函数
解决方法:了解了cv2.imread()函数读取图像后返回值的格式, hsi_h = hsi_image[:, :, 0],hsi_s = hsi_image[:, :, 1],hsi_i = hsi_image[:, :, 2]直接拆分通道。
感想
通过这次实验,我了解到数字图像处理的一些方法应用,也让我对于直方图均衡化以及HSI彩色模型和RGB彩色模型有了更加深刻的理解和认知,数字图像处理是一门十分有用也十分有趣的学科,值得我们去挖掘和探索。