一、二分法
假设有这样一个函数f(x)
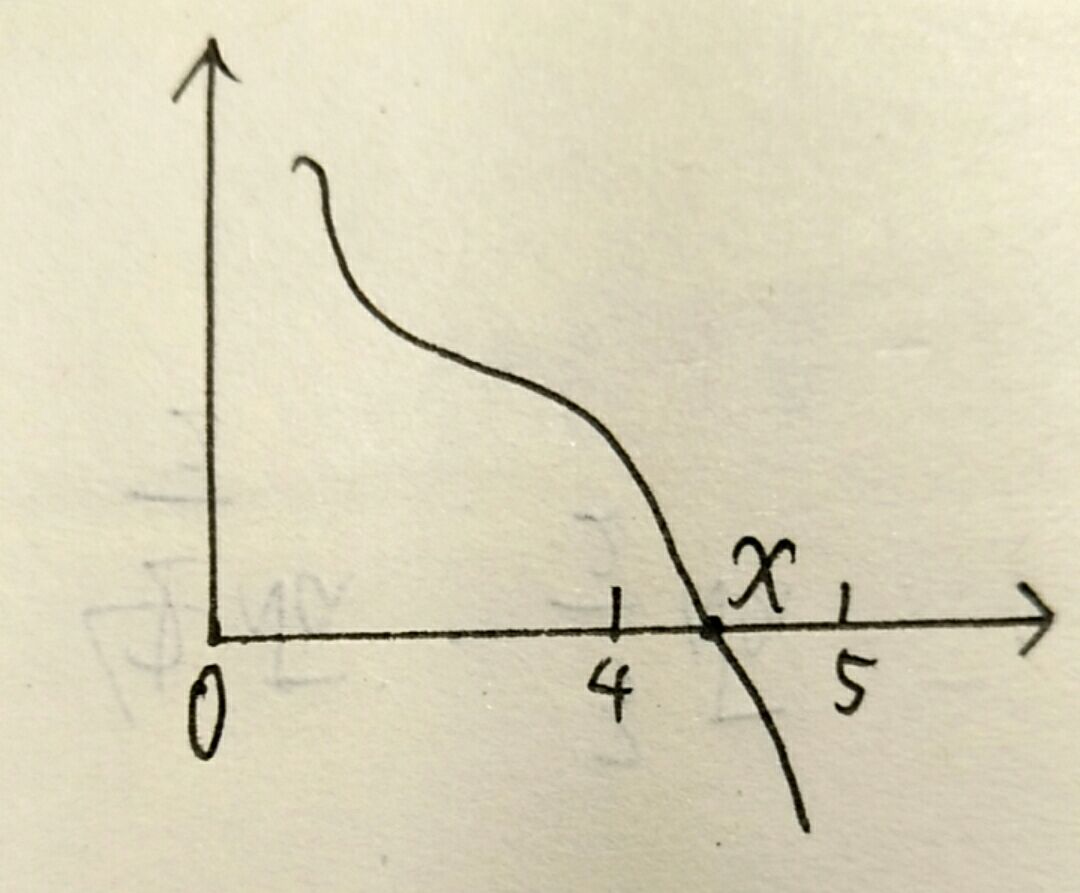
函数与x轴有一个交点(也就是f(a)*f(b)<0,a
直接解显然不合适,那么接下来就轮到二分法出场了。
从图中可以看出4
那么我们只需要不断缩小夹板间的距离就能求出较为精确的ξ值了。
首先,我们取隔离区间的中点(a+b)/2,
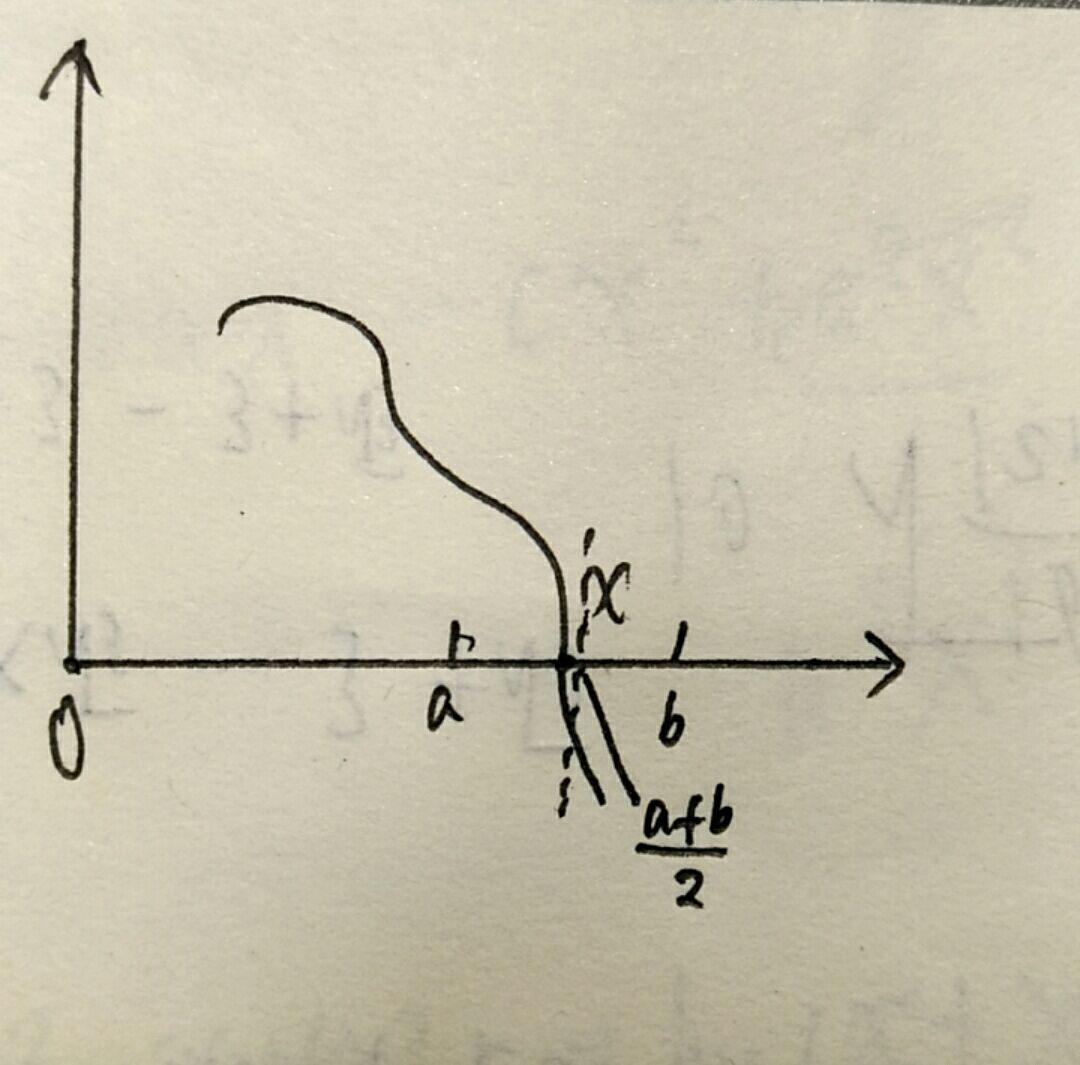
如图,令e=(a+b)/2,如果f(e)=0,那么e就是我们要找的ξ值,如果f(e)和f(a)同号,那么说明这两点都在ξ的同一边,用e替换掉a,
同理,如果f(e)和f(b)同号,用e替换掉b,这样就实现了对ξ的不断逼近,循环n次后误差小于(1/(2^n))*(b-a)。
二、代码实现
废话不多说,直接上代码
1 double dichotomy(int n, double a, double b, double (*f)(double))
2 {
3 double f_a = (*f)(a);
4 double f_b = (*f)(b);
5 int i = 0;
6 while (1)
7 {
8 double e = (a + b) / 2.0;
9 if (i != n)
10 {
11 double f_e = (*f)(e);
12 if (f_e == 0)
13 {
14 return e;
15 }
16 else
17 {
18 if (f_a * f_e > 0)
19 {
20 a = e;
21 }
22 else
23 {
24 b = e;
25 }
26
27 }
28 ++i;
29 }
30 else
31 {
32 return e;
33 }
34
35 }
36 }
二分法的一个例子就是计算根号二(1.4142135623730951),也就是解x^2 - 2 = 0这个方程,代码如下
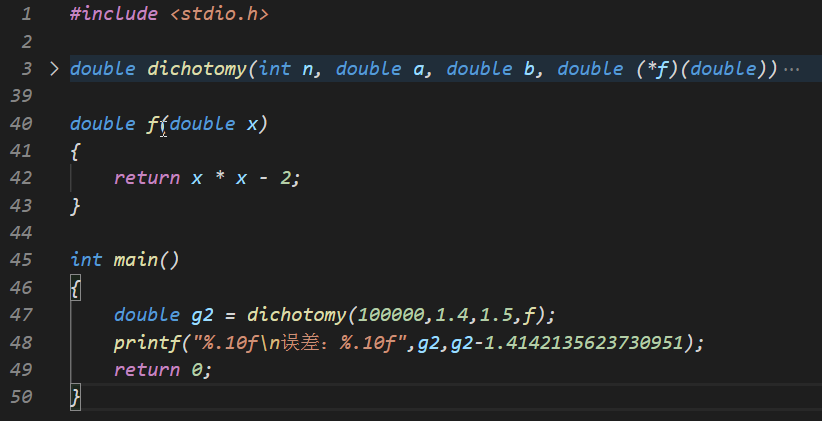
运行效果:
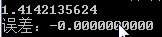
当然,你可以把dichotomy的int n换成long long int n,然后输入一个超大的数,就可以获得更加精确的根号二。
标签:int,double,隔离区,近似,else,二分法,C语言,根号
来源: https://www.cnblogs.com/zhujiangyu/p/13442116.html