Chapter 2 Background and Traditional Approaches

本章主要介绍了一些在深度学习之前用于图数据的机器学习方法。

2.1 Graph Statistics and Kernel Methods

传统的图数据的分类方法和常规的机器学习流程相同，也是先在数据中提取一些统计量或特征，然后用这些特征训练一个标准的分类器。因此，如何提取有效的统计量和特征是一个比较重要的问题。

2.1.1 Node-level statistics and features

首先给出如下的15世纪 Florentine不同家族间的婚姻关系图作为示例，婚姻关系是政治地位的一种反应，Medici家族当时享有较高的地位，结合这个示例我们可以尝试找出哪些统计量能在众多节点中把那些与众不同的节点区分出来。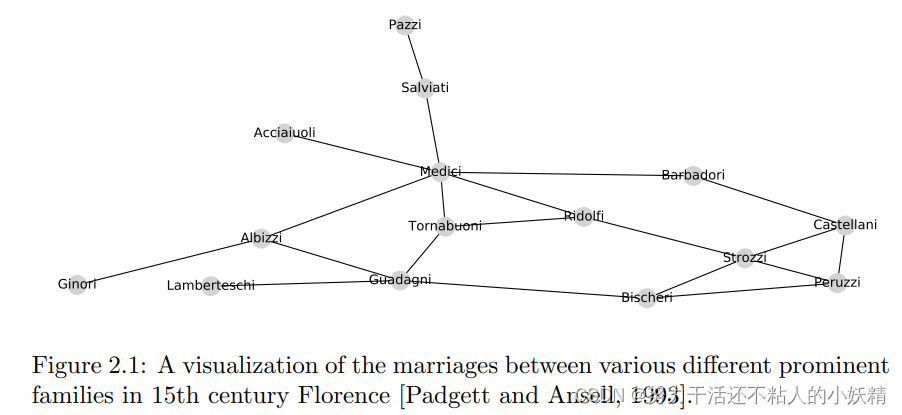

Node Degree. 最直观的特征是节点的度，表示和一个节点相连的边有多少条：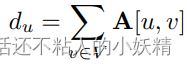

节点的度包含的信息量比较大，在用传统方法处理节点级任务时很常用。例如在示意图中，Medici家族的度就是最大的。

Node centrality. centrality可以有多种不同的定义方式，一种比较常见的是eigenvector centrality，这种特征不仅考虑节点有多少个邻居，还考虑了每个邻居的重要性。具体的，用循环定义的方式给出eigenvector centrality的概念，即每个节点的centrality正比于它的邻居的平均centrality：

其中，$\lambda$是常数。
将所有节点写成向量形式，发现恰好得到邻接矩阵A的特征向量公式：
$\lambda e=Ae$
也就是说，满足定义的centrality应该对应A的一个特征向量。如果我们要求centrality为正值，那么根据Perron-Frobenius定理，满足条件的应该是A的最大特征值对应的特征向量。
从另一个角度来看，eigenvector centrality可以看作在图上做无限长的随机游走时每个节点被访问的概率大小。为了理解这一点，可以借助幂迭代法(Power Iteration)来计算特征值。
Power Iteration是一种通过快速迭代求解特征值的方法，具体介绍可以参考我的博文Power Iteration (幂迭代) 算法与证明。要计算A的最大特征值以及对应的特征向量，只需随机初始化$e$，然后不断左乘A直到收敛：
$e^{(t+1)}=A{e}^{(t)}$
如果我们将e初始化为$e^{(0)}=(1,1,...,1{)}^T$，那么一轮迭代之后得到的结果就是每个节点的度，t步之后，得到的结果$e^{(t)}$就表示到达每一个节点的长度为k的路径的数量。因此，如果迭代次数趋于无穷，得到的结果就正比于在图上做无穷长度的随机游走时每个节点被访问的次数。
此时结合前边的示意图，如果为每个节点计算centrality，会发现Medici对应的值与其他节点更有区分度。

The clustering coefficient. degree和centrality可以描述每个节点的突出程度，但是我们还希望对节点所处的结构特征进行表示，clustering coefficient可以表示一个节点的局部邻域中封闭三角形的比例：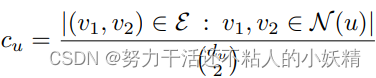

根据定义，分母表示的是节点的邻域中有多少个点对，而分子则表示哪些点对之间是有边的（可以和当前节点构成三角形），因此这个统计量可以表示节点邻域的紧密程度。这个概念还可以扩展到在图中寻找任意的motif或graphlet，此时对于节点的局部模式不要求是三角形，可以是更加复杂的形状，比如指定长度的环，这些同样可以表示图的一些特征。

2.1.2 Graph-level features and graph kernels

前文介绍了节点特征，本节主要介绍在以整张图为单位作为样本时，可以设计哪些特征。
Bag of nodes. 最简单的方式是将节点特征直接聚合，例如，计算前边提到的几种特征的histogram等统计量作为图的特征，缺点是忽略了很多全局结构信息。

The Weisfeiler-Lehman kernel. WL核用于将节点特征进行迭代的邻域聚合，其主要步骤如下：

1. 为每一个节点赋一个初始标签$l^{(0)}(v)$，这里可以使用节点的度。
2. 迭代的通过对当前节点的邻域进行哈希映射的方式为每个节点更新标签
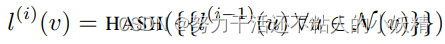
3. 经过K轮迭代之后，得到的标签$l^{(K)}(v)$就已经包含了节点的K-hop邻域的信息。此时再计算这些新的标签的histogram或者其他综合统计量作为图的特征，就已经把图中的结构信息充分考虑进来了。

Graphlets and path-based methods. 另外一种方式是考虑graphlets，即图中的一些小型子图结构的出现频率。最直接的方式是计算图中所有规模的子图的所有可能结构出现的次数（下图是尺寸为3的graphlet示意），但这是一个计算复杂度过高的组合困难问题，不易操作。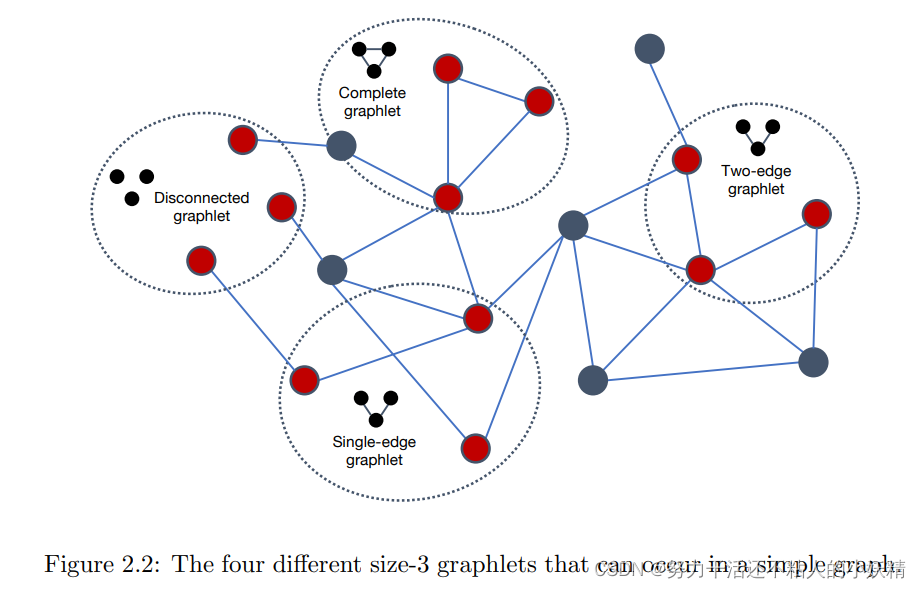

一种替代方式是使用path-based method，不再枚举所有可能的graphlet，而是在图中检测不同类型的path，例如，random walk kernel 首先进行random walk然后计算不同度的序列出现的频率，shortest-path kernel也用了相似的思想，只是将random walk替换为几点间的最短路径。