临时抱佛脚之leetcode刷题笔记

P.S. 自用自用自用！不严谨的个人描述性语句！有理解错误的欢迎大佬指正！

933 最近的请求次数

在迭代列表的时候删除元素，会导致index跳过一个，会有漏掉没有被遍历的元素，因此在迭代列表的时候删元素要从尾部往前面删。

for i in range(len(l)-1,-1,-1):
	operate() # 就像这样

同时933的思想是把不符合条件的元素删除，这样直接返回符合条件的元素个数就可以了！

225 用队列实现栈

双队列实现栈的思想是：最新元素进q2（最新元素要保持在队头），把q1（顺序是栈的顺序！）的元素依次出队到q2，交换q2和q1。

622 设计循环双端队列

设置限定长度的list：

l = [0] * len

通过维护一个列表内元素个数变量count来判断当前列表是否已满。还需要一个头节点。尾结点可以通过头节点+count得到。

496 下一个更大的元素

单调栈：每次新元素入栈，栈内元素都保持有序。但和堆不同，没有全局调整。仅用来解决下一个更大的元素这种问题。
496的中心思想是先遍历一遍可以查找的资料，把所有可能的问题的答案先找到，用HashMap映射。到考试的时候遍历问题，直接找对应的答案就可以了。
找答案逻辑：参考资料list依次入栈，若新入栈元素大于栈底元素，则找到了答案，建立映射；若新入栈元素并没有很大，则继续入栈参考资料list中的新元素，直到符合条件的答案出现，建立映射直到栈空。遍历完参考资料list后若栈内还有元素，则这些元素找不到答案，建立和-1的映射。
在这个过程中，找答案的方法是比当前栈底元素大则出栈，因此整个栈从上到下在数值上是依次变大的，因此是单调栈。

705 设计哈希集合

通过一个哈希函数完成对键的映射。哈希函数一般为$$hash=value\%base$$的形式，base的选择决定了发生冲突的可能性，使用质数避免冲突，当选择的base越大，桶越多，发生冲突的可能性越小。
当发生冲突时有三个解决办法：
1.用各个单独的桶把所有冲突值链起来，如下图所示：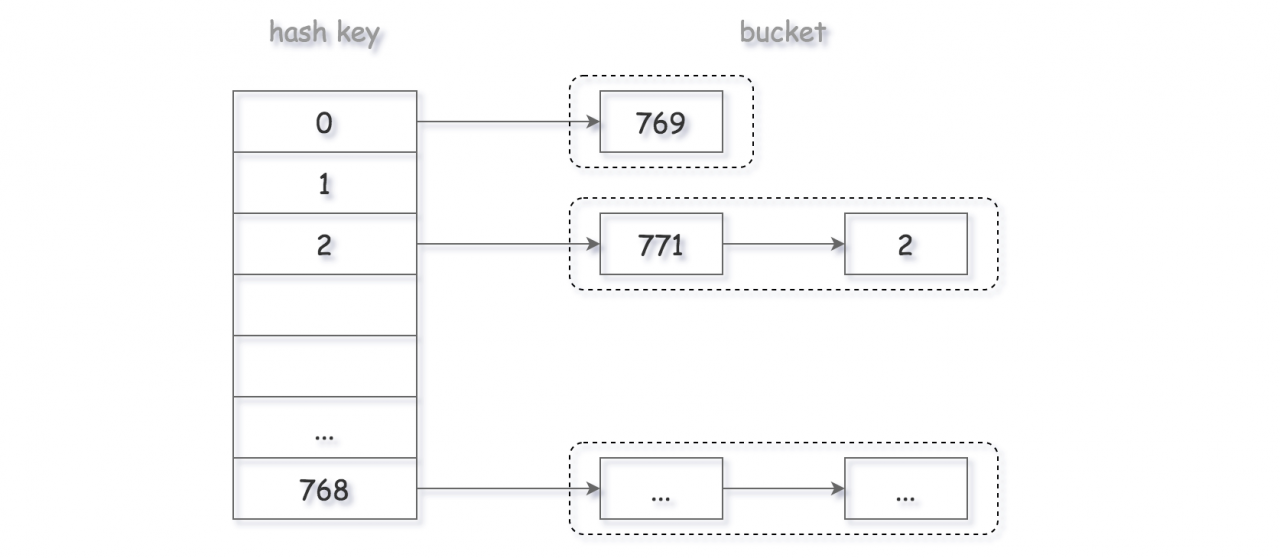

2.用自定义的探查方法找空位放进去
3.双散列法：选择冲突更少的散列函数进行映射
在做题的时候，神奇的事情发生了，我以下面的方式初始化一个限定元素个数的列表：

self.k = [Node(0)] * 769

python为我分配的这个列表里的所有元素都指向同一个地址：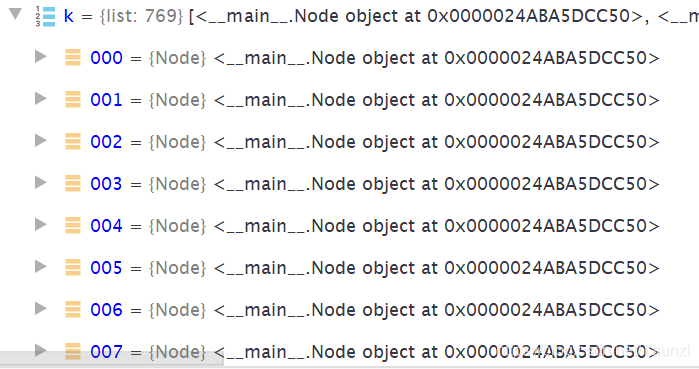

那应该还是要迭代个769次生成列表了！

215 数组中的第K个最大元素

1.复习堆排
以数组的方式存储二叉树，给定这个数组就是已经建立好的无序二叉树了。一个结点$i$的左右孩子的下标分别为$2i+1$和$2i+2$。
堆排的思想是：比如建立好一个最大堆，那么最大的元素在堆顶，则把最大的元素沉到最后的位置->然后重新调整堆，使其满足最大堆的定义，则次大的元素在堆顶，把其放到倒数第二个位置。如此循环之后便得到了一个递增的数列。
假设要排序的元素有n个，则建立最大堆：
（1）从最后一个非叶子结点（下标为n/2-1）开始调整，先取出父结点的值，比较和左右孩子哪个大，把大的赋值给父结点，并拿到这个孩子的下标。
此时可能会使子树不满足最大堆定义，每次调整都要从上到下再调整一遍。针对这个孩子的下标继续看它的左右孩子大小关系，把最开始取出的父结点的值放到它应在的位置（左右孩子都小于父节点），若当前访问的结点已经是叶子节点，则直接把值放入。
（2）元素下标依次递减，得到下一个非叶子结点，继续调整。
排序：
（1）将堆顶元素移到最后，作为已经放好位置的元素。
（2）针对前n-1个元素重新建立最大堆。
但事实上是，用python手动实现堆排做这个题，超时了，哈哈哈哈哈哈哈哈哈
2.改进快排
快排的思想是找到一个分界点，让它的左边的值都小于它，右边的值都大于它。本题目要我们找到第k大的元素，所以在找分界点时，可以判断放好的分界点的位置是在k的左边还是右边，然后在能找到k的那一边继续排就可以了，直到分界点在k上。
快排的具体步骤（参考，写得很好懂诶）：
1.保存分界点元素（可以是第一个），第一个位置就空出来可以填了
2.使用双指针i和j，j从右往左扫，扫到比分界点小的元素就填在空位，这时j这个位置就空出来了
3.i从左往右扫，扫到比分界点大的位置就填在空位j上，这时i的位置空出来了
4.当i<j不成立，则这时i和j的位置就是分界点该放的位置了
5.分别再对数列的左半截和右半截进行这样的操作。递归的结束条件为左端点小于右端点。（当左右端点重合，说明要排的长度只剩下一个了，就不用排了嘛）

692 前K个高频单词

考察一个排序方法。可以用sorted()中的key关键字指定多个排序规则。

a = sorted(mydict.items(), key=lambda x: (-x[1],x[0]))

lambda表达式中的括号表示先对字典的值排序，再对键排序。

141 环形链表

使用快慢指针，若快指针追上了和慢指针相遇了，则链表中存在环。

162 寻找峰值

借鉴了二分搜索的思想缩小解空间。观察题目条件，若找到一个mid值处在上升趋势中（观察mid与其左边元素的关系），则峰值在mid的右边；若mid在下降趋势，则峰值在mid左。当解空间缩小至长度为1时则为答案。
（P.S 162还可以用线性搜索做，不过要观察题目，列表左右两端设为$-\infty$，故只要找到一个元素比右边的元素大就是答案了。怎么就没观察到呢！ ）

209 长度最小的子数组

滑动窗口的思想：先用快指针不断往右扫，直到满足条件。再把慢指针往右移，计算新的答案。与原有的最优解比较得到新的最优解。时间复杂度为$O(n)$，即扫一遍即可。
重点是要维护一个最优解，在得到新的满足条件的窗口时才可以比较。

1456 定长子串中元音的最大数目

也是用滑动窗口做，不过要借鉴的思想是当滑动窗口的大小一定时，移动滑动窗口，两个窗口之间的区别只有移动的步长×2。
比如在本题中，移动步长为1，两个窗口的区别为：第一个窗口的第一个元素和第二个窗口的最后一个元素。所以每次移动后，我们只需要判断：
1、区别1是否为元音，是则最大元音数-1
2、区别2是否为元音，是则最大元音数+1
每次在新窗口里从头计算元音数，活该超时哈！

206 反转链表

我愿意称之为木头脑袋学递归：
一个简单的思想是：当在做结点1时，把剩下的部分当做已经反转好了的，所以需要操作的部分只有结点1和剩下的一大块，以及想一个递归终止条件出来。
Q1：如何操作结点1和排好的一大块呢？
此时，结点1依然指向反向排好的一大块。故结点1.next=一大块。
我们要实现的是一大块.next=结点1，所以等量代换可得结点1.next.next=结点1。
Q2：递归终止条件是什么？
是走到链表的最尾元素，新头.next=最尾元素，这就是最小的反转排好的部分。
（附344（反转字符串）：感觉递归的精髓就是找到一个可重复的操作，一直按某个顺序执行这个操作就会慢慢靠近结果。二是要想到递归结束条件。）

687 最长同值路径

败在以一个遍历的思想去走了，没有想到横过来的路径要怎么整。把原始的一整棵树的每一个结点当做一个子问题，整棵树维护一个最优解变量。子问题的求解方法就比较清晰了，若和相邻左子树元素相同则左路径+1，右边也是同样的。比较当前最优解和左路径+右路径得出的结果。
重点：最优解保存的是左路径+右路径的结果，而递归返回的值是左路径和右路径更大的那一个！（最长路径不能拐弯）

169 多数元素

虽然分治法不明智，但是用这道题练习一下分治法，经典思想是分成两截分别比较各自的众数（多数元素占多于一半，故截成两份也一定是每一份中的众数）
当截出来的长度为1时就把这个数作为这截数组的众数返回，但是没有想到的是当两截返回的众数不同时该如何处理……其实不应该把两个子问题看得太割裂，它们还是处在一个整体中的。正确的处理方法是统计在父数组区间中两个候选者众数各自的出现次数，决定哪个是真正的众数。

53 最大子序和

好你个所谓的简单题！ （不过我要将它封为今天写到的最牛的题，线段树真是太妙了）
本题用分治法维护一棵线段树。从思考如何得到一个区间的最大和入手，最大和（msum）可能是：
-----------不跨越mid元素-----------
1）左子区间的最大和（lsum）
2）右子区间的最大和（rsum）
-------------跨越mid元素-------------
3）左子区间的rsum+右子区间的lsum
（Q：为什么不是lsum+rsum？
A：因为要保持两个区间是粘在一起的）
而对[l,r]，lsum可能为：
1）左子区间的lsum（左子区间的lsum是可能跨越左子区间的mid元素的！）
2）左子区间的所有元素加和（isum）+右子区间的lsum
同理，rsum可能为：
1）右子区间的rsum
2）右子区间的所有元素加和（isum）+左区间的rsum
故针对所有区间，都要维护lsum、rsum、isum、msum这四个变量，而最大区间的msum就是我们要求的答案了！
其实就是多想想测试用例……想想这些结果是怎么被计算出来的

22 括号生成

初步的想法是采用编译原理中规约的思想，当一条路走到尽头了就规约。但其实对一条路走到尽头了是怎样的情况是模糊的（就是序列不合法啊！）。
本题的解分为两个步骤：生成所有可能的序列→判断序列是否合法
1）生成所有可能的序列
采用递归的思想，长度为n的序列是由长度为n-1的序列加上一个’（‘或一个’）'构成的。所以递归体就出来了，当序列长度小于n时加一个括号，递归结束条件为序列长度为n。
2）判断序列是否合法
生成所有可能的序列是耗费时间的，因此当判断当前生成的序列不合法时就应该停止递归了。借鉴使用一个变量来判断当前状态是否合法的思想，观察到左括号永远出现在右括号之前，且在序列生成过程中，右括号数不能多于左括号，生成完成的序列左括号数=右括号。
因此，每扫到一个左括号+1，扫到一个右括号-1，当序列生成过程中标志变量小于1，则不合法；当生成完成后标志变量不为0，也不合法。

78 子集

回溯问题就是要恢复原状态继续递归的DFS。
总结一下回溯问题的解法：
1）形成递归树，找出要传递的参数
2）找递归结束条件
3）在递归树的每一个结点中，能去到下一个结点的选择
4）撤销当前选择，选择另一个去到下一个新结点
5）考虑是否有多余路径的剪枝

46 全排列

当然用上述套路做法是哪道题都做得出的，只是越来越慢，越来越慢慢慢慢慢
这道题我的做法是将每一步已经做出的选择都用list存起来，再不断添加。每一步做出的选择为了不能改变，在每一次递归的时候就都要深拷贝两次，怪不得很慢慢慢慢慢
参考题解的思想：假设现在要填first这个位置，那么我们肯定是用[first+1,n]这些还没有用来填过的元素去填first这个位置。故我们交换first位置的元素和[first+1,n]这个区间的每个元素，填好之后再填下一个位置（递归first+1）。递归回来之后撤销交换操作，再把first位置和[first+1,n]中下一个元素进行交换。

547 省份数量

主要是复习一下并查集。并查集主要由一个union和一个find函数，还有一个记录各个结点的爹的数组组成。初始化时每个结点的爹都是自己。
find是一个回填，维护爹数组的函数。它的函数体如下所示：

def find(index):
	if parent[index]!=index:
		parent[index] = find(parent[index])
	return parent[index]

若当前index位置的数值不等于自身，说明这个结点在外面有了别的爹了。于是find(parent[index])语句相当于一个找出真爹之旅。由于这个函数又有返回值，相当于在找爹之旅的过程中，把整个路径都填上真爹。
union是一个连接两个连通分量真爹的函数。它的函数体如下所示：

def union(index1,index2):
	parent[find(index1)] = find(index2)

两个连通分量的头目连接上了，就是所有结点都连接上了。

322 零钱兑换

先复习记忆化搜索。本题的思想是遍历能用的钱币，查看要凑足（当前钱数-所选钱币面值）最少需要多少枚硬币，再在这个最少的基础上+1。
生成这样一棵搜索树是庞大的，于是把每次需要重复计算的最少需要钱币数放进缓存里，就不用再算一次。具体的放进缓存的方法是使用@functools.lru_cache(maxsize)这个装饰器。（注：maxsize值是缓存输入输出pair数量）
最少需要多少枚硬币的计算逻辑是这样的，返回值需要满足以下的条件：
1）花费的钱币数是合法的。不能花完这个币之后超出了当前要凑的钱数。故当花了钱币之后超出了要凑的钱时，返回-1，当返回值小于1时，不保存当前这个最少需要的钱币数结果。
2）当花了钱币之后刚刚好凑足了要凑的钱时，返回0，这是合法的。判断返回值合法后，判断当前返回值是不是优于最优解。若优，就在当前的返回值上加这一枚用了的钱币，更新最优解，否则也不更新。再把当前最优解返回给上一层。
但是力扣用不了这个装饰器呢，嘿嘿

1217 玩筹码

可恶，一看题解的思路就清晰起来了，我怎么就想不到呢！
若最终目标位置为偶数位，则奇数位移动步数衡为1，偶数位移动步数衡为2；若最终目标位置为奇数位，则偶数位移动步数衡为1，奇数位移动步数衡为2。
需要做的是统计奇数和偶数位筹码的多少，决定最终目标位置为奇数还是偶数，然后统计步数就可以了。

121 买卖股票的最佳时机

一直在想，累计收益这个值是由哪些最优子结构组成的。想来想去只想到卖出天和买入天的差价。不如不从最优子结构入手，从状态转换入手。
自变量是时间。随着时间的不同，在当前时间的可以做出的选择是：在今天持有股票、在今天卖出股票、不动。
1）考虑在今天持有股票，有两种可能：
a、你在昨天已经持有股票了->当前钱数不动
b、你在昨天没有持有股票->以当前时间价格买入（-今天价格）
（maybe你在想，为什么不是当前钱数-今天价格，如果是这样的话，就是允许多次买入卖出的状况了）
2）考虑在今天不持有股票，有两种可能：
a、你在昨天持有股票->以当前时间卖出（钱数+今天价格）
b、你在昨天没有持有股票->当前钱数不动
我们在任意时刻都应该维护这两种选择的当前最优状态，这就是我们要求的最优子结构了。

279 完全平方数

状态转移方程是想出来了……自己的代码中不足的部分是每次都要将所剩的数开方，没有想到这些开方数也可以一次计算多次使用。
题解的思想是针对从1到所求数，分别都求出它们的最优解。求出最优解是遍历完全平方数组，比较使用不同的平方数凑出的结果，当当前平方数比所求数大时，退出循环。

221 最大正方形

重点思路是当前位置的最大正方形面积取决于左边，右边，和斜上角的值，填状态转移矩阵。
若当前位置值为0，则状态矩阵填0；
若当前位置值为1，且左、右、斜上角值都为1，则在状态转移矩阵的左、右、斜上角位置找一个最小的值，加1填上（因为要保证正方形，可不得找最严格的条件）；
若不满足正方形条件，则在状态转移矩阵填1。

208 实现Trie（前缀树）

学习前缀树！它的结构是这样的，一个词由许多结点组成：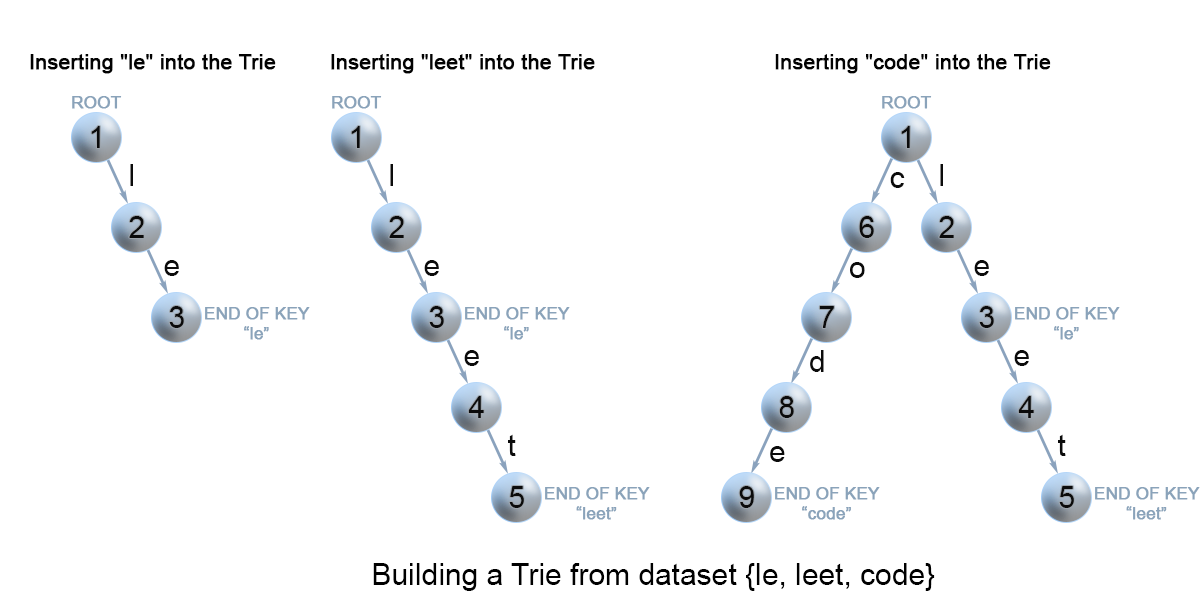

主要是插入结点的操作，若结点存在，则顺移下去；若不存在，则新建结点。我使用了hashmap存放对应的子结点。
（学到了新的数据结构，虽然实现起来是不难的）

3.24，50题撒花✿✿ヽ(°▽°)ノ✿（菜鸡开心.jpg）

207 课程表

学习拓扑排序！
针对每一个结点，若这个结点还没有被扫描过，则将它的状态标记为扫描中，dfs它的所有邻接结点，当它的所有邻接结点被扫描完了，将这个结点标记为扫描完毕。
若要扫的结点状态被标记为扫描中，则说明图中存在环，不存在拓扑排序。

3 无重复字符的最长子串

用字典存储所有出现过的字符位置。如果当前扫到的字符出现过（重复了）且出现的位置比当前最长串开始的位置要后（重复位置在当前最长串里面），把当前最长串开始位置调到重复字符第一次出现的位置之后。
每次扫到不重复的字符时，都将最长串扩张，重新计算最大长度。

25 K个一组翻转链表

翻转：
反转链表需要一个尾部用来做终止条件（普通反转链表的尾部是None，在本地中是tail.next）和一个头部，然后返回新头部（本题中新头新尾都需要返回），使用pre和curr同时移动来实现。
K个一组：
分为K个子链表，每次翻转后需要链接回原链，故需要记录子链表的头部前一个节点和尾部后一个结点。使用头部前一个节点做k次循环寻找尾部结点，若剩余的结点不足k个，则返回我们一开始创造的原链头部的前一个节点。

二叉树的前/中/后续遍历（迭代）

前序：根节点入栈，出栈即访问，然后把右左结点入栈。循环至栈空。
中序：一直往左走，入栈。无左即为中，出栈访问。设为右，一直往左走，……循环以上步骤至栈空。（注：指针指到哪里就入栈到哪里！包括设为右的时候！
后续：根节点入栈，出栈头插入结果数组，把左右结点入栈。循环至栈空。