相关资源下载
目录
碎碎念
第二次上台了。也是拖了最后花几天整的代码。emmmm通宵速成准备上台。
概览
- 动态规划算法设计思想。
- 金罐游戏问题的动态规划解法。
问题
金罐游戏中有两个玩家,A和B,所有的金罐排成一排,每个罐子里都有一些金币, 玩家可以看到每个金罐中有多少硬币。A和B两个玩家交替轮流打开金罐,但是必须从一排的某一端开始挑选,玩家可以从一排罐的任一端挑选一个罐打开。 获胜者是最后拥有更多硬币的玩家。 我们是A玩家,问如何才能使A 收集的硬币数量最大。
假设 B 也是按照“最佳”策略玩,并且 A 开始游戏。
例如:
金罐中金币个数(已排列) | A | B |
4, 6, 2, 3 | 3 | |
4, 6, 2 | 4 | |
6, 2 | 6 | |
2 | 2 | |
9 coins | 6 coins |
金罐中金币个数(已排列) | A | B |
6, 1, 4, 9, 8, 5 | 6 | |
1, 4, 9, 8, 5 | 5 | |
1, 4, 9, 8 | 8 | |
1, 4, 9 | 9 | |
1, 4 | 4 | |
1 | 1 | |
18 coins | 15 coins |
原理
暴力法:
概括问题
如该题,我尝试将问题总结出来,比较麻烦的是这里有A B二者的关系,同时序列起始终止一直在变化,导致一开始也比较难以确定最后一步。
想到序列是动态的,而每一步会减小序列的长度,说明每一段序列很有可能和我们要找的问题息息相关。问题的概括可以回到自然语言问题的表达获取,问题求解A获得的最大金币数,那么我隐藏人物信息,直接将问题概括为求解当前序列下可获得的最大金币数,则问题可以表达为MaxCoins(i,j),其中i是序列起始位置,j是终止位置。尝试是否能找到该问题对应的子问题和递归方程。
递归方程
通过问题和子问题关系找到对应的递归方程,再用递归通过一层层的求解子问题最终找到解。
首先得将问题分解为子问题,找到子问题的关键是找到问题的最后一步,最后一步求解时会用到子问题的解来得到最终问题的解。
在这道题里要求解当前序列下可获得的金币数,应该是当前序列总金币数sum(i,j)减去另一方获得的金币数(也就是下一步的序列【此时另一方在取金罐】获得的金币数,即子问题)。
而下一步的序列取决于当前是取左端金罐还是右端金罐。那么最后一步自然就是取2端金罐。取左端金罐那么下一步序列就会变成从i+1到j序列,取右端金罐那么下一步序列就会变成从i到j-1序列。
如果是最大金币数MaxCoins(i,j),那么就应该是2种情况的最大值,及递归方程为MaxCoins(i,j) = max(sum(i,j)- MaxCoins(i+1,j), sum(i,j)- MaxCoins(i,j-1))。
终止条件
即边界情况。易知剩余第1个金罐pot[i](即i==j)时MaxCoins(i,j)=pot[i]=pot[j]。
动态规划:
相较暴力法,动态规划优化算法的主要步骤就是增加了状态存储过程,即利用数组记忆递归过程的返回值,使得省略重复调用同一递归过程,大大减少资源和时间浪费,提高了算法效率。
这里涉及序列起始和终止位置i j两个参数,自然只能用二维数组MaxCoins[i][j]来实现。因为i<=j所以最终会是个右上三角矩阵,且应该最先填对角线MaxCoins[i][i],再从下到上、从左到有依次填空至最后右上角MaxCoins[0][num-1](共num个金罐),即为最终答案。
动态规划方程即为递归方程:
MaxCoins[i][j] = max(sum(i,j)- MaxCoins[i+1][j], sum(i,j)- MaxCoins[i+1][j])
如题1,金罐数列为pot={4,6,2,3},则MaxCoins[i][j]填表依次如下:
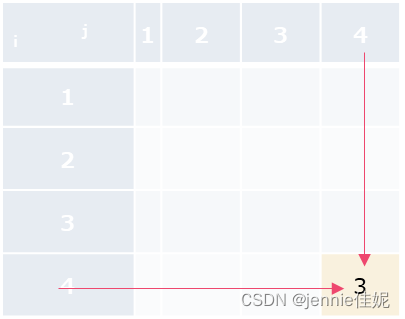
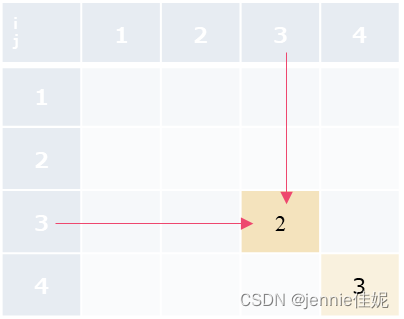
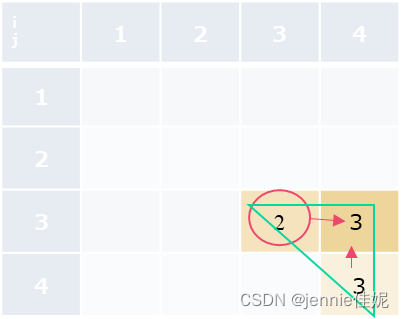
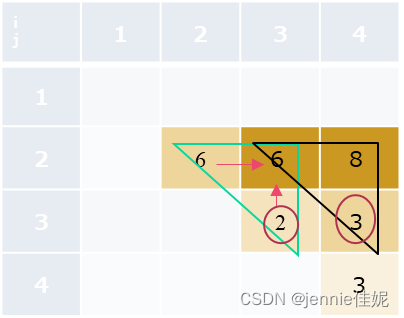
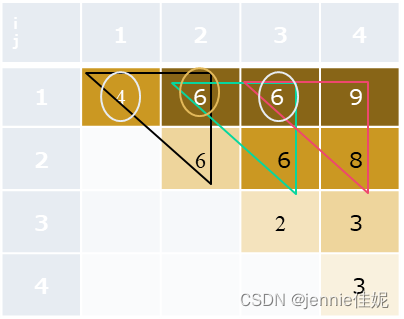
i j | 1 | 2 | 3 | 4 |
1 | 4 | 10 | 12 | 15 |
2 | 6 | 8 | 11 | |
3 | 2 | 5 | ||
4 | 3 |
动态规划方程;
具体分析过程见原理,方程如下:
MaxCoins[i][j] = max(sum(i,j)- MaxCoins[i+1][j], sum(i,j)- MaxCoins[i][j-1])
=sum(i,j)-min(MaxCoins[i+1][j], MaxCoins[i][j-1])
记录A选择的是哪个金罐
蛮力法伪代码
Force(i,j) //从i到j可获得最大金币数
if i==j
return pot[i] //剩余1个直接返回(终止条件)
return max(sum(i,j)-Force(i + 1, j), sum(i,j) - Force(i, j - 1));
动态规划:
由于需要输出A的操作,我在记录状态值的同时也需要记录每个状态值对应的全部操作,而A的操作就是其中计数次操作。我另外开辟同样大小二维字符串数组op[num][num]记录操作。
动态规划伪代码
for i = num to 1 //行倒序
dp[i][i]=pot[i] //填对角线
for j=i+1 to num
dp[i][j]=max(sum(i,j)-dp[i+1][j],sum(i,j)-dp[i][j-1])
set(op[i][j]) //更新操作
对实验给出的数据测试成功:(图1 2)

Figure 1 例1
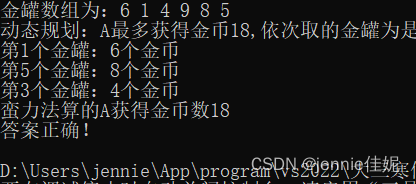
Figure 2 例2
数据处理
小数据模型
随机产生金罐的个数和金币值,对小数据模型利用蛮力法测试算法的正确性,并记录A选择的是哪个金罐;
设定最大金罐数20,最大金币值10,测试成功:(图3)
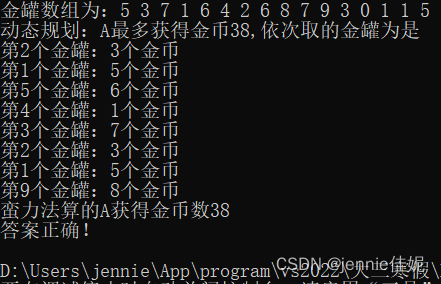
Figure 3 蛮力法小数据规模结果
蛮力法:(图4)
![]()
![]()
![]()
![]()
Figure 4 蛮力法小数据规模运行时间
时间复杂度为O(n),以数据规模为25为基准:(表2 3)
数据规模 | 15 | 20 | 25 | 30 |
实际时间/s | 0.001 | 0.021 | 0.640 | 20.343 |
理论时间/s | 0.000625 | 0.020 | 0.640 | 20.48 |
Table 2 蛮力法不同数据规模算法效率
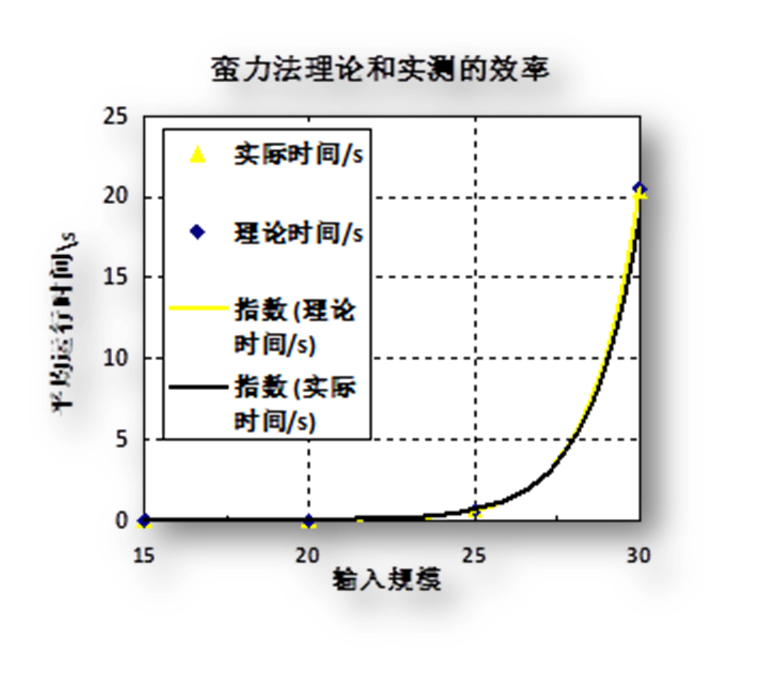
Table 3 蛮力法
随机不同数据规模
随机产生金罐的个数和金币值,对不同数据规模(n的值)测试算法效率,并与理论效率进行比对,请提供能处理的数据最大规模,注意要在有限时间内处理完;(图5)
![]()
![]()
![]()
![]()
Figure 5 动态规划不同数据规模运行时间
尝试能处理的数据最大规模为22925:(图6)
![]()
Figure 6 动态规划最大处理数据量
以下以数据规模为5000为基准:(表4 图7)
数据规模 | 5000 | 10000 | 15000 | 20000 |
实际时间/s | 0.211 | 0.845 | 1.909 | 3.336 |
理论时间/s | 0.211 | 0.844 | 1.899 | 3.376 |
Table 4 动态规划不同数据规模算法效率
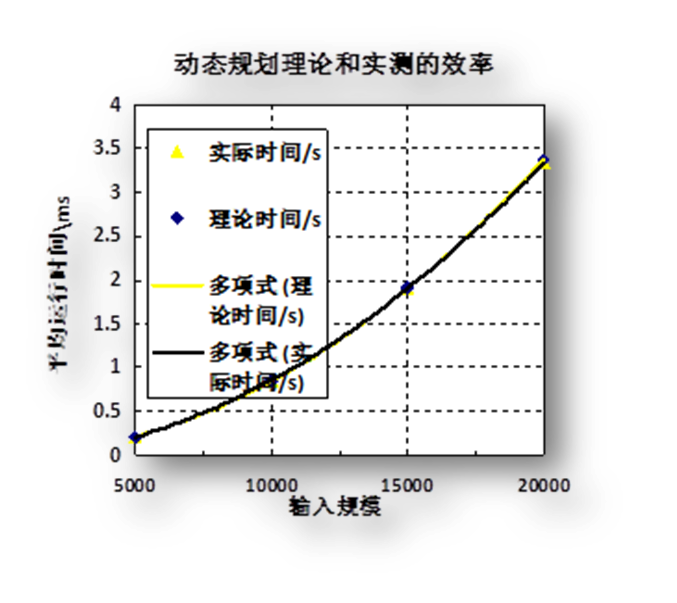
Figure 7 动态规划
优化
蛮力法:
关于优化方面,蛮力法较之动态规划,主要的算算法效率开销是重复递归和递归开销。那么我们也可以同样利用状态数组进行优化。
蛮力法优化伪代码
Force(i,j) //从i到j可获得最大金币数
if i==j
return pot[i] //剩余1个直接返回(终止条件)
if MaxCoins[i][j] //如果已经递归调用过了,则直接返回记录值
return MaxCoins[i][j]
MaxCoins[i][j] = max(Sum[i][j] - Force(i + 1, j), Sum[i][j] - Force(i, j - 1))
return MaxCoins[i][j]
那么优化后的蛮力法在面对大数据时,除了可能数据量过大而开辟的递归栈帧过多导致栈溢出或大量的空间开销,就可以实现大数据处理了。
数据规模 | 5000 | 10000 | 15000 |
运行时间/s | 0.949 | 5.267 | 17.382 |
Table 5 蛮力法优化运行时间
动态规划:
空间效率提高(二维改一维)求和预处理
在这里主要尝试对其空间效率进行优化,因为我们最终只需要dp[0][num-1]右上角这个数值,而每一次数组填数只需要要到其左边和下边的数,那么我们就可以把二维状态数组压缩为一维状态数组,将后面用不到的数不断覆盖。同时也改为现在准备阶段对不同求和记录。
动态规划优化后伪代码
for i = num to 0 //行倒序填写
for j = i + 1 to num //倒三角
dp2[j] = Sum[i][j] - min(dp2[j], dp2[j - 1]);
避免求和开销
另外关于求和问题,我与热心的马铭鹤同学探讨,发现可将求解问题改为当前序列获得相对最大金币(即当前2人金币之差)而实现避免这个求和环节。即此时的状态方程为
relMaxCoins[i][j] = max(pot[i]- relMaxCoins[i+1][j], pot[j]- relMaxCoins[i][j-1])
总结
通过本次实验,我尝试了使用蛮力法(简单重复递归)和动态规划解决金罐问题,在该过程中我加深了对于动态规划算法的理解和运用。我认识到动态规划其实是在简单重复递归的逻辑增加状态数组,通过对状态数组的求解而免去重复递归的资源和时间消耗,从而获得解。
动态规划算法的关键就是将问题分解为子问题,并找到两者之间的状态方程。分解子问题的方法是找到最后一步。
另外通过蛮力法(时间复杂度O(2n))和动态规划(时间复杂度O(n2))的实际运行时间,加深对二者运算效率的理解。
在算法优化上,蛮力法也可借鉴动态规划的状态进行记录,避免重复调用,改进后可处理大数据但空间开销还是较大。动态规划求和步骤可提前做,同时在空间效率上可将二维数组压缩为一维数组。而将问题改为求当前序列相对最大金币值可避免求和开销。