向量范数的几何直观理解和等价定义——如何从几何上定义向量范数？

【一.向量范数的几何直观理解】
\quad我们知道，一个函数：$f:R^n\mapsto R$ 被称为$R^n$空间的一个范数,如果它满足以下三条性质：（以下以$\Vert \cdot \Vert$来代表这个函数）
\quad(1)正定性：$\Vert x\Vert \ge 0,\forall x\in R^n$，且：$\Vert x\Vert =0⟺x=0;$
\quad(2)齐次性：$\Vert cx\Vert =|c|\cdot \Vert x\Vert ,\forall x\in R^n,c\in R;$
\quad(3)三角不等式：$\Vert x+y\Vert \le \Vert x\Vert +\Vert y\Vert ,\forall x,y\in R^n;$

\quad接下来，我们将从几何角度理解范数：首先，在有一个范数的情况下，我们可以在$R^n$空间中画出一个单位球$S\triangleq \{x|x\in R^n,\Vert x\Vert \le 1\}$.为了有一个简单的直观理解，我们给出二维情形下，几个常见范数的单位球图像：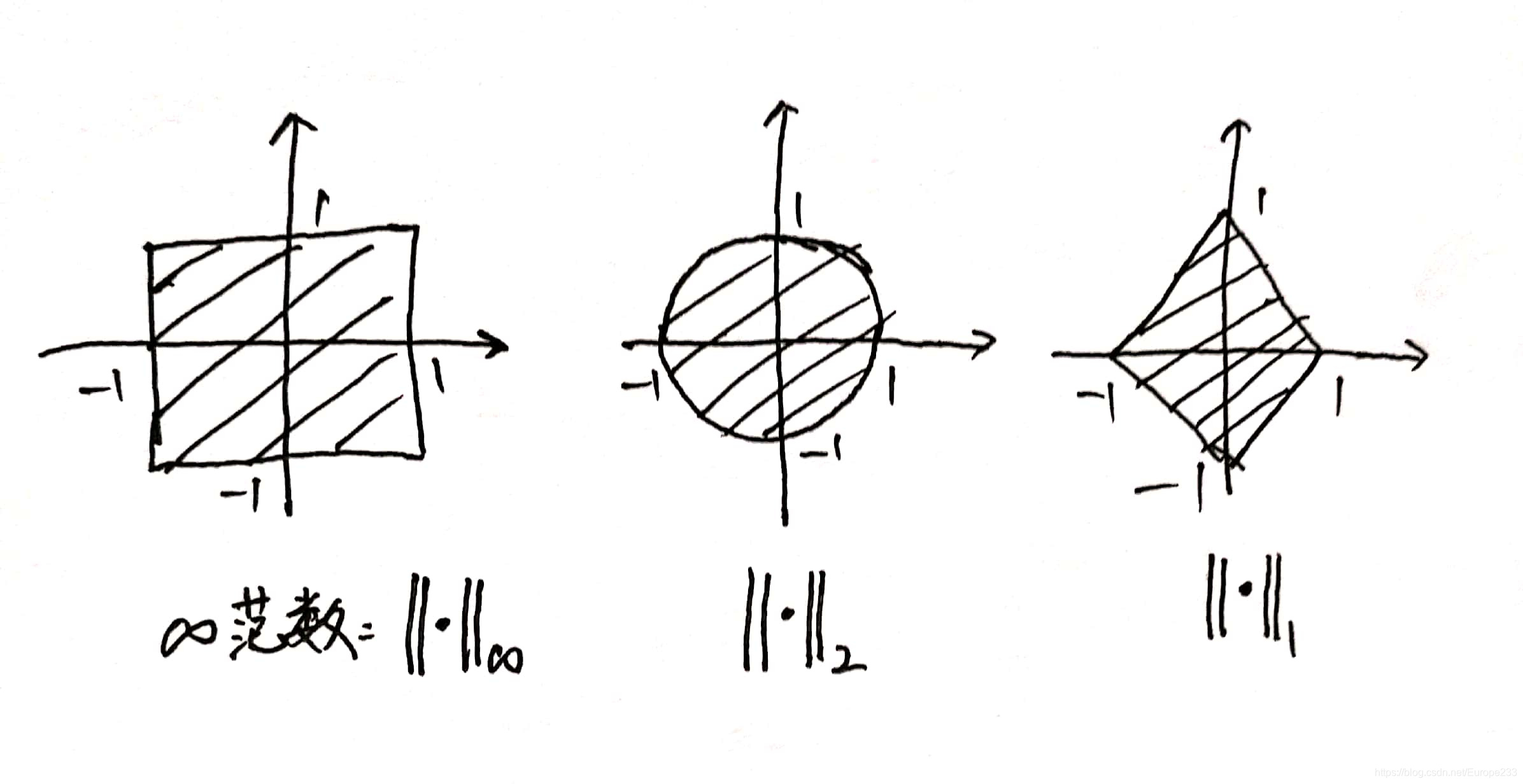

\quad这个单位球显然有以下几个性质：
\quad(1)关于原点对称，即$\forall x\in S,$均有$-x\in S;$
\quad(2)是一个有界闭集，且零向量0是它的一个内点；
\quad(3)是一个凸集：这点由范数满足的三角不等式保证；

\quad范数的几何直观理解就是，如果一个非零向量$x$的端点落在这个单位凸球的边界上，那么$\Vert x\Vert =1$；否则，如果$ax$的端点落在这个单位凸球的边界上，那么$\Vert x\Vert =|\alpha |$.

【二.从几何上定义向量范数】
\quad一个重要结论是：几何上，一个范数和一个满足以上三个条件的凸球一一对应。也就是说，范数能定义一个单位凸球；反过来，如果有了一个满足以上三条性质的凸集，那么可以唯一定义一个向量范数。

\quad假设我们有了一个满足以上三个性质的凸集$C$，定义一个映射：
\quad${\Vert \cdot \Vert }_B:R^n\mapsto R:\Vert x\Vert =sup\{t\ge 0|tx\in C{\}}^{-1}$
\quad那么这个映射就是该凸集定义的一个向量范数。

\quad哈哈，上面这个式子是否很难理解呢？其实它理解起来很简单，和之前范数的几何理解一样：在我们定义这样一个凸集之后，如果一个非零向量$x$的端点落在这个凸集的边界上，那么$\Vert x\Vert =1$；否则，如果$ax$的端点落在这个凸集的边界上，那么$\Vert x\Vert =|\alpha |$.

\quad我们需要证明：这样定义的这个映射满足范数定义中的三条性质，这样才能说这个映射是一个向量范数。
\quad证明：
\quad(1)正定性：由定义，${\Vert x\Vert }_B\ge 0,\forall x\in R^n$自然地满足。由于零向量0是集合$C$的一个内点，也就是说存在一个0的小领域包含于C，因此显然：${\Vert x\Vert }_B=0⟺x=0;$
\quad(2)齐次性：$\forall x\in R^n,c\in R,$
${\Vert cx\Vert }_B=sup\{t\ge 0|tx\in C{\}}^{-1}=|c|\cdot sup\{t\ge 0|tx\in C{\}}^{-1}=|c|\cdot {\Vert x\Vert }_B$
\quad(3)三角不等式：
\quad设 $x,y\in R^n$,如果 $x,y$ 都为0，显然三角不等式成立；
\quad如果$x,y$至少有一个不为0，那么:
\quad$\frac{x+y}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}=\frac{{\Vert x\Vert }_B}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}\frac{x}{{\Vert x\Vert }_B}+\frac{{\Vert y\Vert }_B}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}\frac{y}{{\Vert y\Vert }_B}$
由${\Vert \cdot \Vert }_B$定义： $\frac{x}{{\Vert x\Vert }_B}\in C,\frac{y}{{\Vert y\Vert }_B}\in C.$
再联系到$\frac{{\Vert x\Vert }_B}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}+\frac{{\Vert y\Vert }_B}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}=1$,$C$是一个凸集，所以：
\quad$\frac{x+y}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}\in C$,于是${\Vert \frac{x+y}{{\Vert x\Vert }_B+{\Vert y\Vert }_B}\Vert }_B\le 1$,于是${\Vert x+y\Vert }_B\le {\Vert x\Vert }_B+{\Vert y\Vert }_B;$

综上，证毕。

从上面我们看到了：一个向量范数和一个$R^n$空间的一个凸集一一对应。所以我们有了另一种定义向量范数的方式：画一个凸集即可（当然，这个凸集要满足上面说的几条性质），然后我们就可以说，看：我定义了一个向量范数。

很酷，不是吗？