隐马尔可夫前向后向算法---盒子和球模型

题目

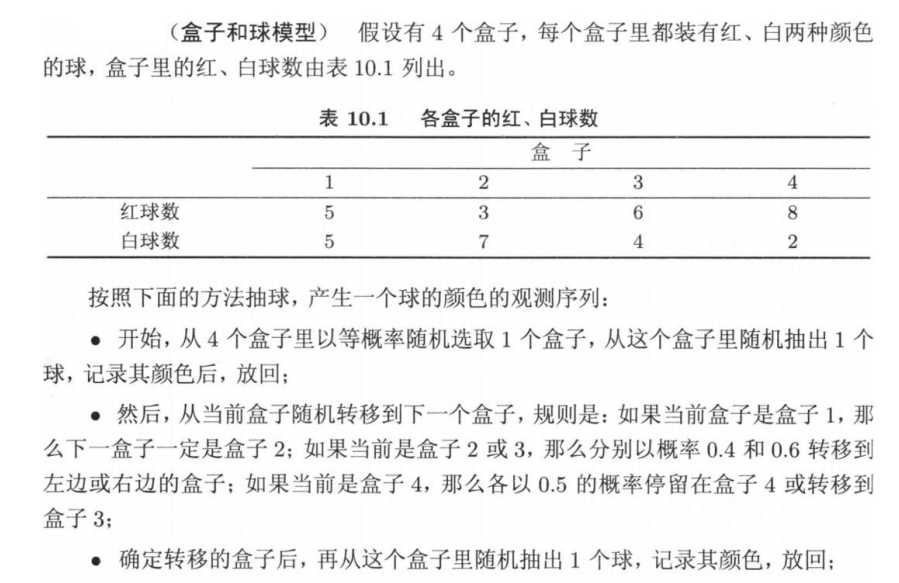
1、用前向算法求抽取四次，抽到球颜色序列为 O=(红，红，白，白)的概率
2、用后向算法求抽取四次，抽到求颜色序列为 O=(白，白，红，红)的概率
要求：要求上传明确的计算过程截图

状态图

思路

代码

#盒子和球模型
from numpy import *
import numpy as np

#盒子对应状态集合Q={盒子1，盒子2，盒子3，盒子4}
#观测集合V={红，白}

#状态转移概率分布
A=np.array([[0,1,0,0],
            [0.4,0,0.6,0],
            [0,0.4,0,0.6],
            [0,0,0.5,0.5]])
#观测概率分布
B=np.array([[0.5,0.5],
            [0.3,0.7],
            [0.6,0.4],
            [0.8,0.2]])
#初始概率分布
pai=np.array([0.25,0.25,0.25,0.25])

#前向算法
def HMM_forward():   
    #抽到的球的颜色序列O=(红，红，白，白)
    o=np.array([0,0,1,1])

    # 初始化
    T=len(o)
    #B的维数，即盒子数量
    Box_Num=shape(B)[0]

    #建立alpha矩阵
    alpha=np.zeros(T*Box_Num).reshape(Box_Num,T)

    #时刻1是红色，隐藏状态是1、2、3、4的概率
    for i in range(Box_Num):
        alpha[i][0]=pai[i]*B[i][o[0]]

    # 迭代3次，每次填充一个时刻的alpha[i]
    sigma=0
    for j in range(T-1):
        for i in range(Box_Num):
            for k in range(Box_Num):
                #时刻j+2到达状态o[j+1]全概率
                sigma+=alpha[k][j]*A[k][i]
            #盒子i,时刻j+2（时刻2，3，4）的概率
            alpha[i][j+1]=sigma*B[i][o[j+1]]
            sigma=0

    # 终止
    #对最外层[]内最大的块做块与块的运算，同时去掉最外层[]
    Pro=np.sum(alpha,axis=0)
    print("α矩阵：")
    print(alpha)
    #观测为O=(红，红，白，白)的概率
    print("观测为O=(红，红，白，白)的概率是 %.8f "%Pro[T-1])

#后向算法
def HMM_backward():
    #抽到的球的颜色序列O=(白，白，红，红)
    o=np.array([1,1,0,0])
    # 初始化
    T=len(o)
    Box_Num=shape(B)[0]

    #建立beta矩阵
    beta=np.zeros(T*Box_Num).reshape(Box_Num,T)
    #时刻4各个隐藏状态后向概率都为1
    for i in range(Box_Num):
        beta[i][0]=1

    # 迭代3次，每次填充一个时刻的beta[i]
    sigma=0
    t=T
    for j in range(T-1):
        t -= 1
        for i in range(Box_Num):
            for k in range(Box_Num):
                sigma+=A[i][k]*B[k][o[t]]*beta[k][j]
            beta[i][(j+1)]=sigma
            sigma=0

    print("β矩阵：")
    print(beta)


    # 终止
    sigma=0
    for i in range(Box_Num):
        sigma+=pai[i]*B[i][o[0]]*beta[i][T-1]
    #观测为O=(白，白，红，红)的概率
    print("观测为O=(白，白，红，红)的概率是 %.8f "%sigma)


if __name__=='__main__':
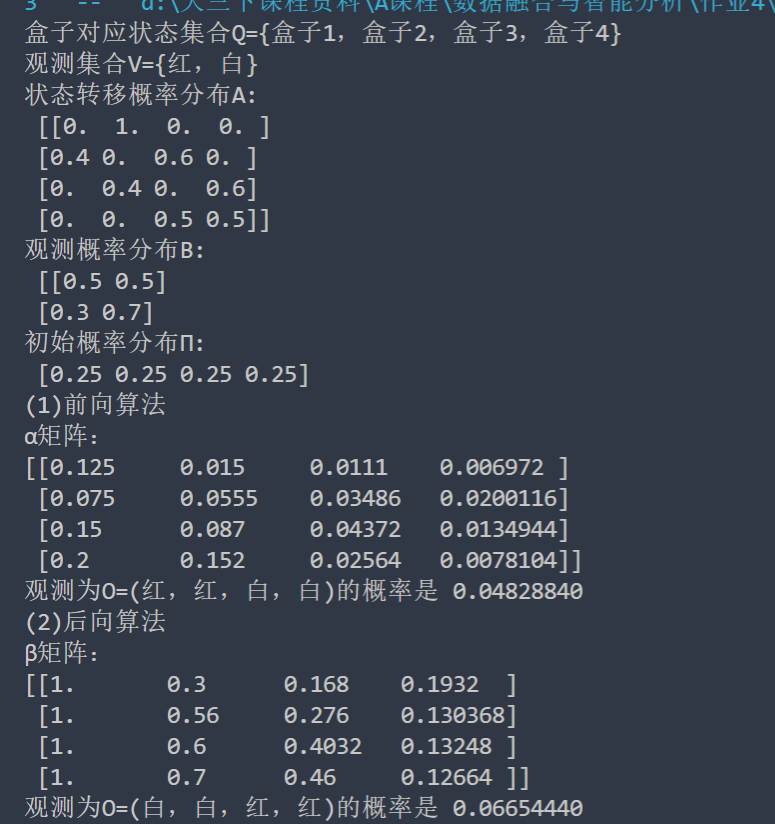
    print("盒子对应状态集合Q={盒子1，盒子2，盒子3，盒子4}")
    print("观测集合V={红，白}")
    print("状态转移概率分布A:","\n",A)
    print("观测概率分布B:","\n",B)
    print("初始概率分布Π:","\n",pai)
    print("(1)前向算法")
    HMM_forward()
    print("(2)后向算法")
    HMM_backward()

答案（运行结果）