基于密度的算法

基于密度的算法的核心思想是根据样本点某一邻域内的邻居数定义样本空间的密度，这类算法可以找出空间中形状不规则的簇，并且不用指定簇的数量。算法的核心是计算每一点处的密度值，以及根据密度来定义簇。

1.DBSCAN算法理论

DBSCAN算法是一种基于密度的算法，可以有效的处理噪声，发现任意形状的簇。它将定义为样本点密集的区域，算法从一个种子样本开始，持续向密集的区域生长直至到达边界。
算法使用了两个人工设定的参数$\epsilon$和$M$，前者是样本点的领域半径，后者是定义核心点的样本数阈值。下面介绍他们的概念。
假设有样本集$X=\{x_1,x_2,...,x_N\}$，样本点$x$的$\epsilon$邻域定义为样本集中与该样本的距离小于等于$\epsilon$的样本构成的集合
$$N_{\epsilon }(x)=\{y\in X:d(x,y)\}$$
其中，$d(x,y)$是两个样本之间的距离，可以采用任何一种距离定义。样本的密度定义为它的$\epsilon$邻域的样本数：
$$\rho (x)=|N_{\epsilon }(x)|$$
密度是一个非负整数。核心点定义为数据集中密度大于指定阈值的样本点，即如果
$$\rho (x)\ge M$$
则称$x$为核心点，核心点是样本分布密集的区域。样本集$X$中所有的核心点构成的集合为$X_c$，非核心点构成的集合为$X_{n}c$。如果$x$是非核心点，并且它的$\epsilon$邻域内存在核心点，则称$x$为边界点，边界点是密集区域的边界。如果一个点既不是核心点也不是边界点，则称之为噪声点，噪声点是样本稀疏的区域。
如果$x$是核心点，$y$在它的$\epsilon$邻域内，则称$y$是从$x$直接密度可达的。对于样本集中 的一组样本$x_1,x_2,...,x_n$，如果$x_i$${}_{+}$${}_1$是从$x_i$直接密度可达的，则称$x_n$是从$x_i$可达的，密度可达是直接密度可达的推广。
对于样本集中的样本点$x,y$和$z$,如果$y$和$z$都从$x$密度可达，则称他们是密度相连的，根据定义，密度相连具有对称性。
基于上面的概念可以给出簇的定义。样本集$C$是整个样本集的一个子集，如果它满足下列条件：对于样本集$X$中的任意两个样本$x$和$y$，如果$x\in C$,且$y$是从$x$直接密度可达的，则$y\in C$；如果$x\in C,y\in C$，则$x$和$y$是密度相连的，则称集合$C$是一个簇。
根据簇的定义可以构造出聚类算法，具体做法是从某一核心点出发，不断 向密度可达的区域扩张，得到一个包含核心点和边界点的最大区域。这个区域中惹事两点的密度相连。
假设有样本集$X$,聚类算法将这些样本划分成$K$个簇以及噪声点的集合，其中$K$由算法确定。每个样本要么属于这些簇中的一个，要么是噪声点。定义变量$m_i$为样本$x_i$所属的簇，如果它属于第$j$个簇，则$m_i$的值为$j$,如果它不属于这些簇中的任意一个，即是噪声点，则其值为-1，$m_i$就是聚类算法的返回结果。变量$k$表示当前的簇号，每发现一个新的簇其值加1。聚类算法流程如下：
第一阶段，初始化
计算每个样本的邻域$N_{\epsilon }(x_i)$
令$k=1,m_i=0$,初始化待处理样本集合$I=\{1,2,...,N\}$
第二阶段，生成所有的簇
循环，当$I$不为空
从$I$中取出一个样本$i$，并将其从集合中删除
如果$i$没被处理过，即$m_i=0$
初始化集合$T=N_{\epsilon }(x_i)$
如果$i$为非核心点
令$m_i=-1$，暂时标记为噪声
如果$i$为核心点
令$m_i=k$，将当前簇编号赋予该样本
循环，当$T$不为空
从集合$T$中取出一个样本$j$并从该集合中将其删除
如果$m_i=0$或者$m_i=-1$
令$m_i=k$
如果$j$是核心点
将$j$的邻居集合$N_{\epsilon }(x_i)$加入集合$T$
结束循环
令$k=k+1$
结束循环

算法的核心步骤是依次处理每一个还未标记额的点，如果是核心点，则将其邻居点加入到连接的结合浩总，反复扩张，直到找到一个完整的簇。
在实现时有几个问题需要考虑，第一个问题是如何快速找到一个点的所有邻居集合，可以用R树或者KD树等数据结构加速，第二个问题是参数$\epsilon$和$M$的设定，$\epsilon$的取值在有的时候非常难以确定，而它对聚类的结果有很大影响。$M$值的选择有一个指导性原则，如果样本向量是$n$维的，则$M$的取值至少为$n+1$。
DBSCAN无须指定簇的数量，可以发现任意形状的簇，并且对噪声不敏感。其缺点是聚类的质量受距离函数的影响很大，如果数据维度很高，将面临维度灾难的问题。参数$\epsilon$和$M$的设定有时候很困难。

2.DBSCAN算法的sklearn实现

在sklearn库中包含着各种各样的聚类算法，下面我们实现DBSCAN算法并实现其他聚类算法与DBSCAN算法形成对照。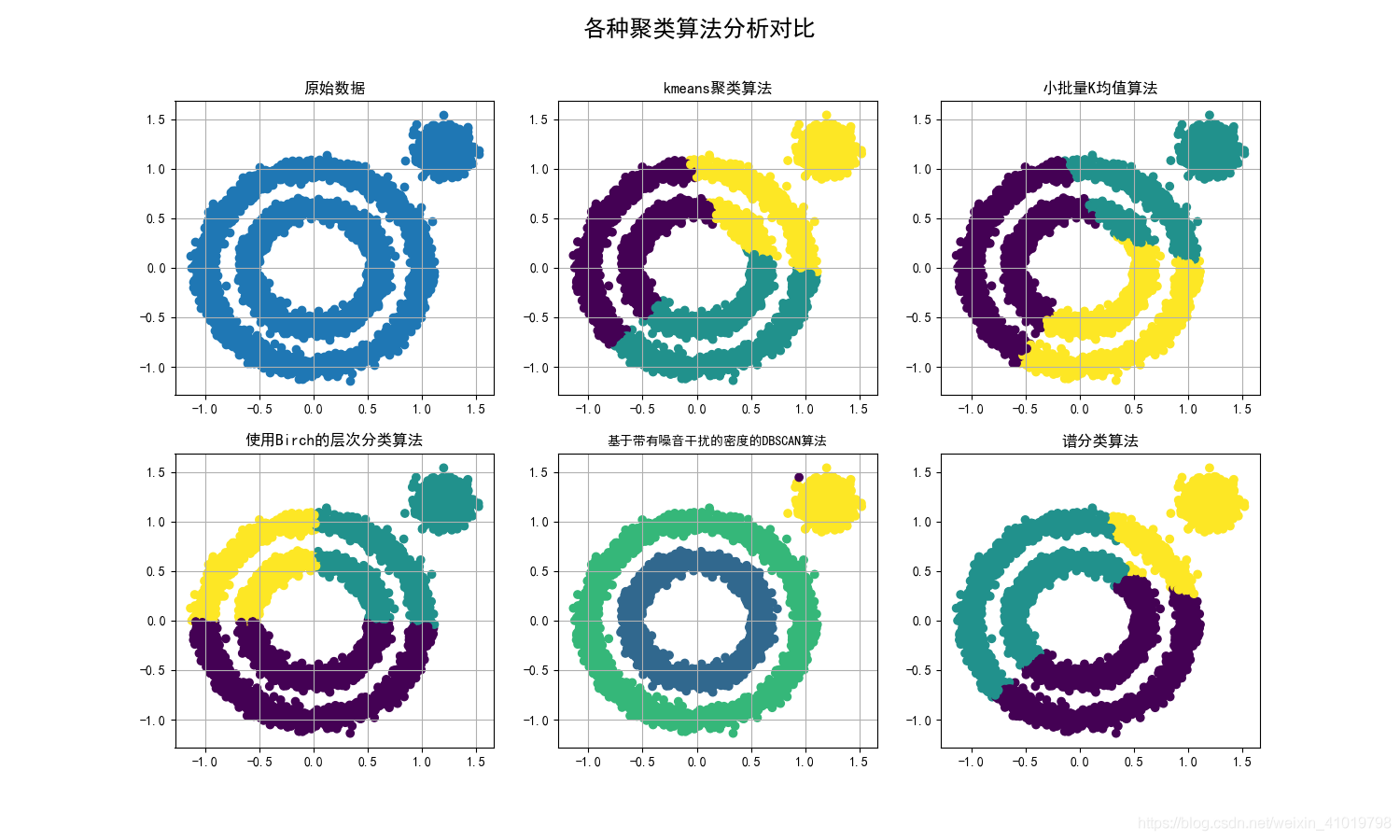

五种算法代码实现

import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn.cluster import KMeans
from sklearn import datasets
# 小批量K均值算法
from sklearn.cluster import MiniBatchKMeans
# 使用Birch的层次分类方法
from sklearn.cluster import Birch
# 基于带有噪音干扰的密度分类法
from sklearn.cluster import DBSCAN
# 谱分类，需要计算基于rbf距离的相似矩阵
from sklearn.cluster import SpectralClustering
x1, _ = datasets.make_circles(n_samples=5000, factor=.6, noise=0.05)
x2, _ = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2, 1.2]], cluster_std=[[.1]], random_state=9)
data = np.concatenate((x1, x2), axis=0)
plt.figure(figsize=(15, 9))
plt.subplot(231)
# 解决中文无法显示问题
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False
# 原始数据作图
plt.scatter(data[:, 0], data[:, 1])
plt.title("原始数据")
plt.grid(True)
plt.subplot(232)
#使用Kmeans聚类进行分析
result = KMeans(n_clusters=3, random_state=9).fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=result)
plt.title("kmeans聚类算法")
plt.grid(True)
# 小批量K均值算法
plt.subplot(233)
result = MiniBatchKMeans(n_clusters=3, random_state=9).fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=result)
plt.title("小批量K均值算法")
plt.grid(True)
# 使用Birch的层次分类方法
plt.subplot(234)
result = Birch(n_clusters=3).fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=result)
plt.title("使用Birch的层次分类算法")
plt.grid(True)
# 基于带有噪音干扰的密度分类法,这种方法不需要制定分类类别，但是需要制定距离和每一簇的最小样本数。
plt.subplot(235)
result = DBSCAN(eps=0.1, min_samples=10).fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=result)
plt.title("基于带有噪音干扰的密度的DBSCAN算法",fontsize=10)
plt.grid(True)
# 谱分类，需要计算基于rbf距离的相似矩阵
plt.subplot(236)
result = SpectralClustering(n_clusters=3).fit_predict(data)
plt.scatter(data[:, 0], data[:, 1], c=result)
plt.title("谱分类算法")#需要计算基于rbf距离的相似矩阵
plt.suptitle(u'各种聚类算法分析对比', fontsize=18)
plt.show()

请大家多多指教！
注：原理参考《机器学习与应用》雷明著，清华大学出版社