邻接表无向图的深度优先遍历C/C++代码实现

图的链式存储：

图的链式存储有多种，有邻接表、十字链表和邻接多重表，下面注意说明邻接表。

邻接表：

邻接表由两部分组 成：表头结点表和边表。

例：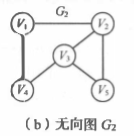

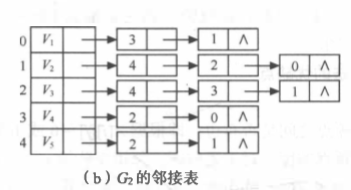
深度优先遍历：

为了避免同一顶点被访问多次，在遍历图的过程中，必须记下每个已访问过的顶点。 为此，设一 个辅助数组visited[n] , 其初始值置为"false"或者0, 一旦访问了顶点V, 便置visited[i]为"true" 或者1。
以该图为例：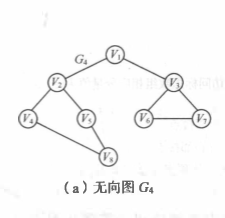

代码如下：

#include<stdio.h>

#define MVNum 100
typedef char OtherInfo;
typedef char VerTexType;

//邻接表存储结构
typedef struct ArcNode			//边结点
{
	int adjvex;
	struct ArcNode *nextarc;
	OtherInfo info;
}ArcNode;
typedef struct VNode			//顶点信息
{
	VerTexType data;
	ArcNode *firstarc;
}VNode, AdjList[MVNum];
typedef struct                  //邻接表
{
	AdjList vertices;
	int vexnum, arcnum;
}ALGraph;
int LocateVex(ALGraph G, char v);
void LinkAL(ALGraph &G, int i, int j);


//邻接表创建无向图
void CreateUDG(ALGraph &G)
{
	G.vexnum = 8;						//输入总顶点数和边数
	G.arcnum = 9;
	G.vertices[0].data = 'v1';			//输入顶点信息
	G.vertices[0].firstarc = NULL;
	G.vertices[1].data = 'v2';
	G.vertices[1].firstarc = NULL;
	G.vertices[2].data = 'v3';
	G.vertices[2].firstarc = NULL;
	G.vertices[3].data = 'v4';
	G.vertices[3].firstarc = NULL;
	G.vertices[4].data = 'v5';
	G.vertices[4].firstarc = NULL;
	G.vertices[5].data = 'v6';
	G.vertices[5].firstarc = NULL;
	G.vertices[6].data = 'v7';
	G.vertices[6].firstarc = NULL;
	G.vertices[7].data = 'v8';
	G.vertices[7].firstarc = NULL;

	int i, j;							//输入边信息
	i = LocateVex(G, 'v1');
	j = LocateVex(G, 'v2');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v2');
	j = LocateVex(G, 'v4');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v2');
	j = LocateVex(G, 'v5');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v5');
	j = LocateVex(G, 'v8');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v4');
	j = LocateVex(G, 'v8');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v1');
	j = LocateVex(G, 'v3');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v3');
	j = LocateVex(G, 'v6');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v3');
	j = LocateVex(G, 'v7');
	LinkAL(G, i, j);
	i = LocateVex(G, 'v6');
	j = LocateVex(G, 'v7');
	LinkAL(G, i, j);

}

//建立边
void LinkAL(ALGraph &G, int i, int j)
{
	ArcNode *p1;
	p1 = new ArcNode;
	p1->adjvex = j;
	p1->nextarc = G.vertices[i].firstarc;						  //头插法
	G.vertices[i].firstarc = p1;

	ArcNode *p2;
	p2 = new ArcNode;
	p2->adjvex = i;
	p2->nextarc = G.vertices[j].firstarc;
	G.vertices[j].firstarc = p2;
}

//确定顶点在顶点表数组中的下边，并返回
int LocateVex(ALGraph G, char v)
{
	for (int i = 0; i < G.vexnum; i++)
	{
		if (G.vertices[i].data == v)
		{
			return i;
		}
	}
}

//打印输出
void printGraph(ALGraph G)
{
	for (int i = 0; i < G.vexnum; i++)
	{
		printf("%d :", i);
		printf("v%d ->", i + 1);

		ArcNode *p;
		p = G.vertices[i].firstarc;
		while (p != NULL)
		{
			printf("%d->", p->adjvex);
			p = p->nextarc;
		}
		printf("\n");
	}
}

//邻接表深度优先遍历
bool visited[MVNum];
void DFS_AL(ALGraph G, int v)
{
	printf("v%c->", G.vertices[v].data);
	visited[v] = true;
	ArcNode *p;
	p = G.vertices[v].firstarc;
	while (p != NULL)
	{
		int w = p->adjvex;
		if (!visited[w])
		{
			DFS_AL(G, w);
		}
		p = p->nextarc;
	}
}


int main()
{
	ALGraph G;
	CreateUDG(G);
	printGraph(G);

	int v = 0;			//从0号开始遍历
	DFS_AL(G, v);
}

运行结果：