机器学习之线性回归模型的代价函数是凸函数的证明

凸函数的定义

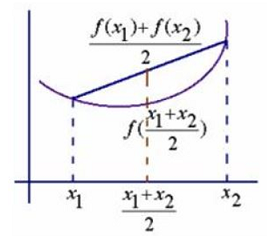
• 对区间[a,b]上定义的函数 f ，若它对区间中任意两点x1，x2均有 f((x1 + x2) / 2) <= (f(x1) + f(x2))/2则称 f 为区间[a,b]上的凸函数
• U型曲线的函数如 f(x)=x²，通常是凸函数
  

判别

• 对实数集上的函数，可以通过求二阶导数来判别：
• 若二阶导数在区间上非负，则称为凸函数；若恒大于0，则称为严格凸函数
  

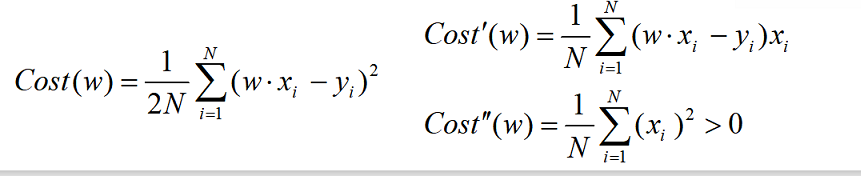
好处

我们喜欢凸函数是因为该函数只有一个全局最有解，这样的代价函数，我们在进行模型训练，操作梯度下降的时候，会很准确，模型总会走到全局最优解。