1. 分类
矩阵分解(decomposition, factorization)是多半将矩阵拆解为数个三角形矩阵(triangular matrix),依使用目的的不同,可分为几类。
与线性方程解法相关的矩阵分解
2. LU分解
在线性代数与数值分析中,LU分解是矩阵分解的一种,将一个矩阵分解为一个下三角矩阵和一个上三角矩阵的乘积,有时需要再乘上一个置换矩阵。LU分解可以被视为高斯消元法的矩阵形式。在数值计算上,LU分解经常被用来解线性方程组、且在求反矩阵和计算行列式中都是一个关键的步骤。
2.1 定义
PartialPivLU<MatrixXd> lu(HPH_T);
HPH_T_inv = lu.inverse();

2.2 存在性和唯一性

2.3 实例



2.4 应用

3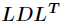 分解
分解
实际问题中,当求解方程组的系数矩阵是对称矩阵时,则用下面介绍的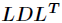 分解法可以简化程序设计并减少计算量。
分解法可以简化程序设计并减少计算量。
从定理可知,当矩阵A的各阶顺序主子式不为零时,A有唯一的Doolittle分解A= LU。矩阵U的对角线元素Uii 不等于0,将矩阵U的每行依次提出,

下面将U分解为
定理:若对称矩阵A的各阶顺序主子式不为零时,则A可以唯一分解为A=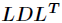 ,这里
,这里

L^T为L的转置矩阵。
当A有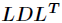 分解时,利用矩阵运算法则及相等原理易得计算ljk和dk的公式为
分解时,利用矩阵运算法则及相等原理易得计算ljk和dk的公式为
将对称正定矩阵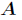 通过分解成
通过分解成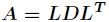 ,其中
,其中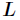 是单位下三角矩阵,
是单位下三角矩阵,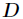 是对角均为正数的对角矩阵。把这
是对角均为正数的对角矩阵。把这
一分解叫做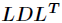 分解,是Cholesky分解的变形。对应两边的元素,很容易得到
分解,是Cholesky分解的变形。对应两边的元素,很容易得到
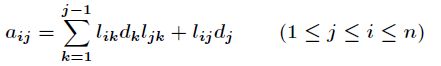
由此可以确定计算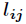 和
和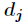 的公式如下
的公式如下
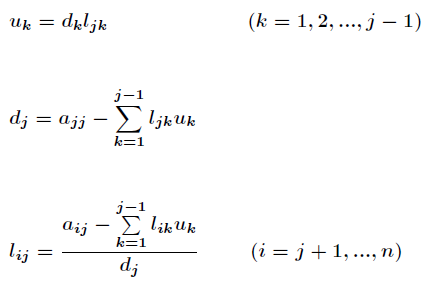
在实际计算时,是将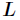 的严格下三角元素存储在
的严格下三角元素存储在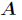 的对应位置上,而将
的对应位置上,而将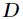 的对角元存储在
的对角元存储在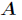 的对应的对角位置上。
的对应的对角位置上。
类似地求解线性方程组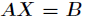 的解步骤如下
的解步骤如下
(1)对矩阵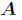 进行分解得到
进行分解得到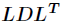
(2)求解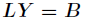 ,得到
,得到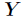
(3)求解 ,得到
,得到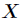
4 Cholesky分解
定义: cholesky分解是一种将任意n阶 对称正定矩阵A 分解成下三角矩阵L的一种方法:
其中,L称为Cholesky因子。如果L的对角元均为正数,则L是唯一确定的。
Cholesky分解对于解决带有 对称正定系数矩阵A 的线性问题非常有效。在计算机中,直接求解
时间复杂度是很高的,用cholesky法对A提前变换之后再计算会有效降低复杂度。计算方法如下:
等价于

例题
用cholesky方法求解线性方程组Ax=b,其中

显然

再求: