Lecture 2: Learning to Answer Yes/No

Perceptron

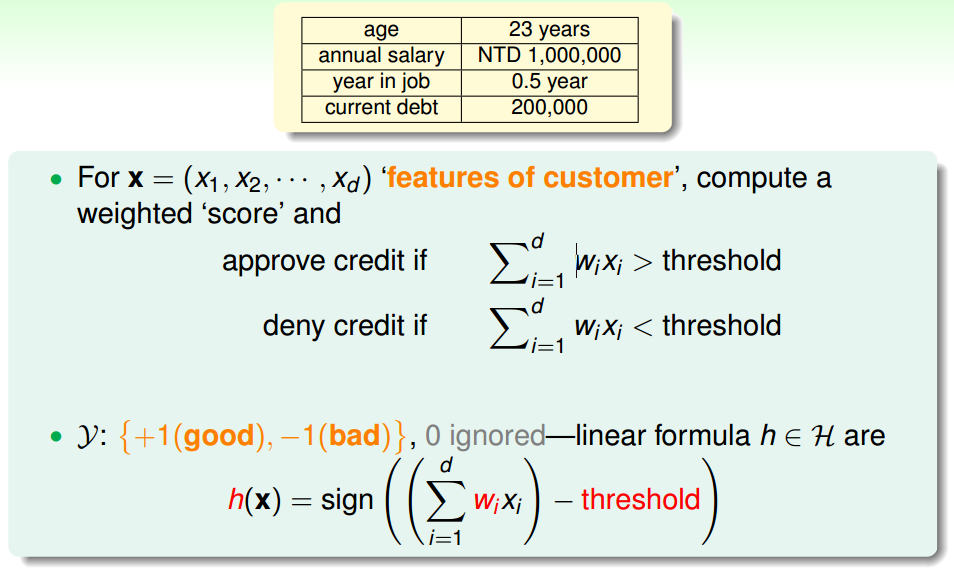
A Simple Hypothesis Set: the ‘Perceptron’

感知器类比神经网络，threshold类比考试60分及格

Vector Form of Perceptron Hypothesis

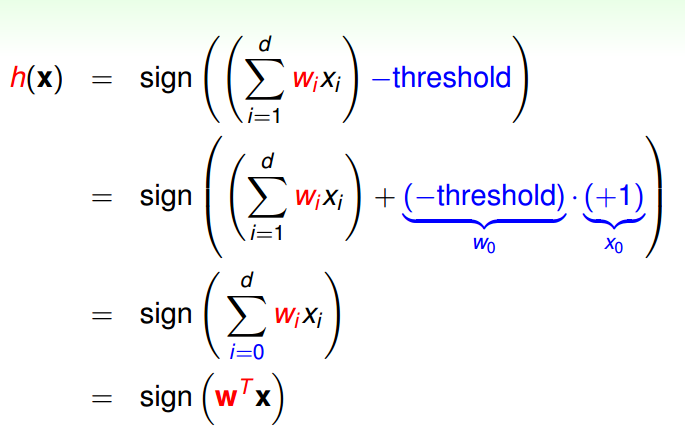
each ‘tall’ $W$represents a hypothesis h & is multiplied with ‘tall’ $X$—will use tall versions to simplify notation

Perceptrons in $R^2$

Fun time

Select $g$from $H$

遍历是不现实的，所以还是迭代吧

Perceptron Learning Algorithm

A fault confessed is half redressed.

因为$w_t^T x_{n(t)}=\lVert w_t \rVert \lVert x_{n(t)} \rVert \cos(w_t,x_{n(t)})$,所以当二者夹角大于90°的时候，内积为-，反之为+

Fun time

说明了什么含义 ？ ② 为什么不对？

Implementation

start from some $w_0$(say, 0,并不是随机的初始化), and ‘correct’ its mistakes on $D$next can follow naïve cycle (1, · · · , N) or precomputed random cycle

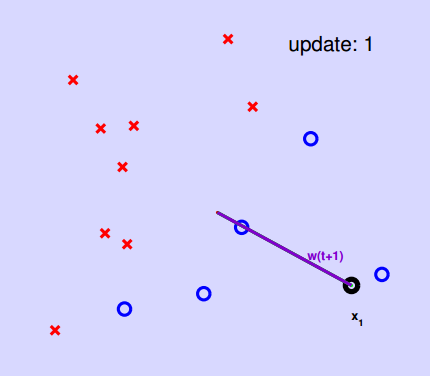
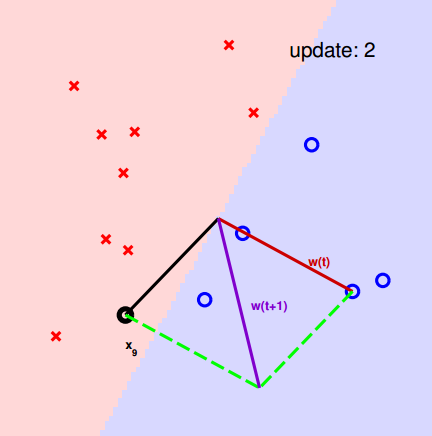
(note: made $x_i \gg x_0 =1$for visual purpose) Why ?

Issues of PLA

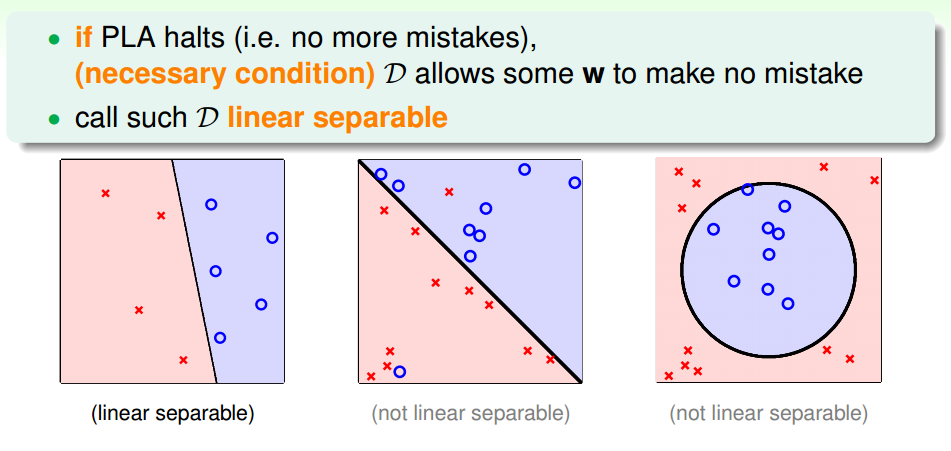
Linear Separability

assume linear separable $D$,does PLA always halt?

halts！

因为 $\frac{w_f^T w_T}{\lVert w_f \rVert \lVert w_T \rVert}<= 1$,所以T肯定有上限

PLA Fact: $w_t$Gets More Aligned with $w_f$

$w_t$appears more aligned with $w_f$after update really?

PLA Fact: $w_t$Does Not Grow Too Fast

$$\begin{align*} w_f^Tw_T &\ge w_f^Tw_{T-1}+\min_{n}y_nw_f^Tx_n\\ &\ge w_fw_0+T\min_n y_n w_f^Tx_n\\ &\ge T\min_ny_n w_f^Tx_n\\ &\ge \rho T \lVert w_f \rVert^2 \tag{A} \end{align*}$$
$$\begin{align*} \lVert w_T\rVert ^2 & \le \lVert w_{T-1} \rVert^2 +\max_n \lVert y_n x_n\rVert\\ & \le \lVert w_0 \rVert^2+T\max\lVert y_n x_n\rVert^2\\ & \le T\max\lVert y_n x_n\rVert^2\\ & \le TR^2 \tag{B} \end{align*}$$
推导过程中需要注意的是， $w_0=0$，然后将 (A)、 (B)代入即可得答案为 ②

得到是上限，而且无法准确求出，因为$w_f$未知
即使$w_0\ne0$也是能证明有上限的

特性

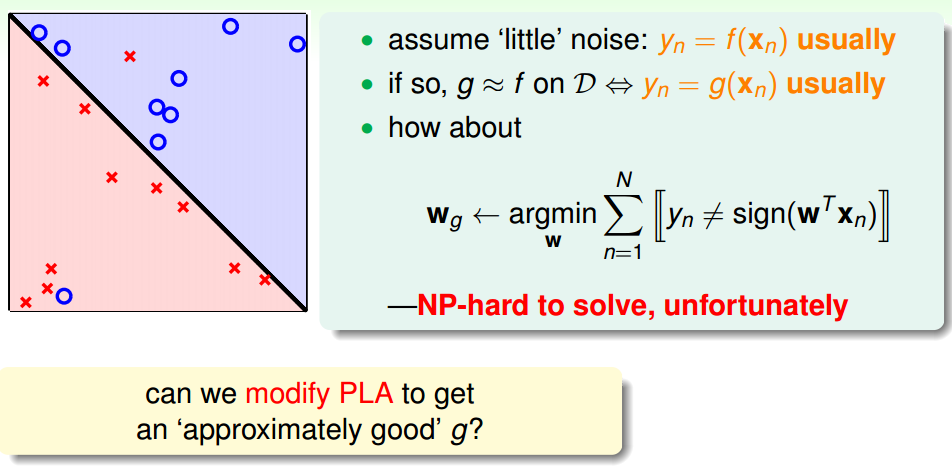
Learning with Noisy Data

NP难问题

Pocket Algorithm

modify PLA algorithm (black lines) by keeping best weights in pocket