回归评估指标(MSE,RMSE,MAR,R-Squared)

均方误差(mean squared error,MSE)

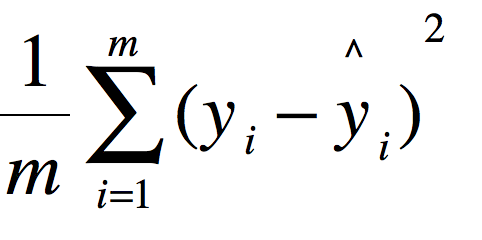
其中 $y_i-\widehat{y_i{}}$ 为测试集上真实值-预测值

均方误差是反应估计量与被估计量之间差异的一种程度，换句话说，参数估计值与参数真值之差的平方期望值。MSE可以评价数据的变化程度，MSE的值越小，说明册页模型描述实验数据具有更好的精确度。

python:

import numpy as np

def mse(y_test, y_predict):
    return np.mean((y_test-y_predict)**2)

均方根误差(root mean squared error,RMSE)

均方根误差亦称标准误差，是均方误差的算术平方根。换句话说，是观测值与真值（或模拟值）偏差（而不是观测值与其平均值之间的偏差）的平方与观测次数n比值的平方根，在实际测量中，观测次数n总是有限的，真值只能用最可信赖（最佳）值来代替。标准误差对一组测量中的特大或特小误差反应非常敏感，所以，标准误差能够很好地反映出测量的精密度。这正是标准误差在工程测量中广泛被采用的原因。因此，标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值同真值之间的偏差。

python：

rmse = np.sqet(mse(y_test, y_predict))

平均绝对误差(mean absolute error,MAE)

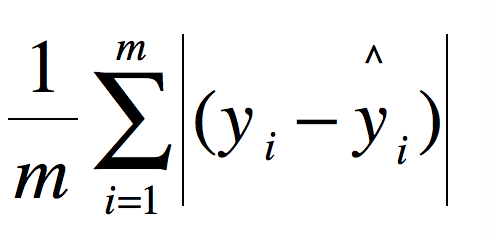
观测值与真值值的误差绝对值的平均值

与MSE的区别在于MSE先对偏差做了一次平方，这样，如果误差的离散度高，即，如果最大偏差值大MSE就放大了

RMSE > MAE 一组正数的平均数的平方小于每个数的平方和的平均数

python：

def mae(y_test, y_predict):
    return np.mean(np.abs(y_test-y_predict))

RMSE和MAE有局限性:同一个算法模型,解决不同的问题,不能体现此模型针对不同问题所表现的优劣 ,因此不同实际应用中,数据的量纲不同,无法直接比较预测值,因此无法判断模型更适合预测哪个问题

R Squared

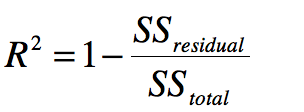
其中分子是Residual Sum of Squares分母是Total Sum of Squares

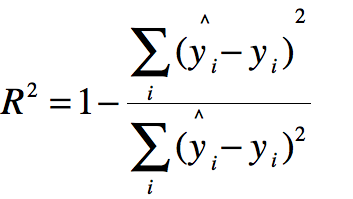
分母为使用模型预测产生的错误，分子为使用 $ｙ＝\overline{ｙ}$ $y=\overline{y}$ 预测产生的错误,在机器学习领域称这种模型为基准模型(Baseline Model)

自己的模型预测产生的错误/基础模型预测生产的错误,表示自己的模型没有拟合住的数据,因此 $R^2{}$ 可以理解为自己的模型拟合住的数据

$R^2{}$ ≤ 1,越大越好,当自己的预测模型不犯任何错误时为1,当我们的模型等于基准模型时为0,当值小于0时,说明学习到的模型还不如基准模型.即数据可能不存在线性关系

公式变形:

python:

def r2(y_test, y_predict):
    return 1-mse(y_test,y_predict)/np.var(y_test)

对于这些评估指标

sklearn可直接调用,只需导入:

from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error

原文链接：https://blog.csdn.net/lyp_1020k/article/details/110440588