搭建深度学习框架（三）：通用神经网络框架搭建

在上一节，我们实现了一维神经网络框架的搭建。但是那种框架只适合一个输入特征的情况，并不能实现通用，本节将在一维框架的基础上实现通用框架的搭建，并且添加了模型保存和加载的代码。
通用模型各节点的实现代码如下，具体实现原理可看注释：
基础节点作为父类。

class Placeholder(Node):
    """
    作为x,k,b,weights和bias这类需要赋初始值和更新值的类
    """
    def __init__(self,name=None,is_trainable=True):
        
        Node.__init__(self,name=name,is_trainable=is_trainable)
        
        
    def forward(self,value=None):
        
        if value is not None: self.value = value
        
    def backward(self):
        
        self.gradients[self] = np.zeros_like(self.value).reshape((self.value.shape[0],-1))
        
        for n in self.outputs:
           
            self.gradients[self] += n.gradients[self].reshape((n.gradients[self].shape[0],-1))  #没有输入。
            
class Linear(Node):
    
    def __init__(self,x=None,weight=None,bias=None,name=None,is_trainable=False):
        
        Node.__init__(self,[x,weight,bias],name=name,is_trainable=is_trainable)
        
    
    def forward(self):
        
        k, x, b = self.inputs[1],self.inputs[0],self.inputs[2]
        
        self.value = np.dot(x.value,k.value) + b.value.squeeze()
      
    def backward(self):
        
        k, x, b = self.inputs[1],self.inputs[0],self.inputs[2]
        
        self.gradients[k] = np.zeros_like(k.value)
        self.gradients[b] = np.zeros_like(b.value).reshape((len(np.zeros_like(b.value))))
        self.gradients[x] = np.zeros_like(x.value)
        
        for n in self.outputs:
            
            gradients_from_loss_to_self = n.gradients[self] 
            self.gradients[k] += np.dot(gradients_from_loss_to_self.T,x.value).T
            self.gradients[b] += np.mean(gradients_from_loss_to_self,axis=0,keepdims=False).reshape((len(np.zeros_like(b.value))))
            self.gradients[x] += np.dot(gradients_from_loss_to_self,k.value.T)

class Sigmoid(Node):
    
    def __init__(self,x,name=None,is_trainable=False):
        
        Node.__init__(self,[x],name=name,is_trainable=is_trainable)
        self.x = self.inputs[0]
    
    def _Sigmoid(self,x):
        
        return 1. /(1+np.exp(-1*x))
    
    def forward(self):
        
        self.value = self._Sigmoid(self.x.value)
        
    def partial(self):
        
        return self._Sigmoid(self.x.value) * (1 - self._Sigmoid(self.x.value))
    
    def backward(self):
        
        self.gradients[self.x] = np.zeros_like(self.value)
     
        for n in self.outputs:
            gradients_from_loss_to_self = n.gradients[self] #输出节点对这个节点的偏导，self：指的是本身这个节点
            self.gradients[self.x] += gradients_from_loss_to_self*self.partial()
            

class ReLu(Node):
    def __init__(self,x,name=None,is_trainable = False):
        Node.__init__(self,[x],name=name,is_trainable=is_trainable)
        self.x = self.inputs[0]
        
    def forward(self):
        self.value = self.x.value*(self.x.value > 0)
    
    def backward(self):
        self.gradients[self.x] = np.zeros_like(self.value)
        
        for n in self.outputs:
            gradients_from_loss_to_self = n.gradients[self]
            self.gradients[self.x] += gradients_from_loss_to_self*(self.x.value > 0)
            
class MSE(Node):
    
    def __init__(self,y_pre,y,name,is_trainable=False):
        
        Node.__init__(self,[y_pre,y],name=name,is_trainable=is_trainable)
        self.y_pre, self.y = self.inputs[0],self.inputs[1]
        
  
    def forward(self):
        y = self.y.value.reshape(-1,1)
        y_pre = self.y_pre.value.reshape(-1,1)
       
        assert(y.shape == y_pre.shape)

        self.m = self.inputs[0].value.shape[0]
        self.diff = y - y_pre

        self.value = np.mean(self.diff**2)
        
  
    def backward(self):
        
        
        self.gradients[self.y] = (2 / self.m) * self.diff
        self.gradients[self.y_pre] = (-2 / self.m) * self.diff  
            

使用上一节讲解的拓扑排序算法实现各个节点的排序。

import random
"""
使用拓扑排序找到网络节点的前向计算顺序（反向传播反过来就行）
"""
def toplogical(graph):
    
    sorted_graph_nodes = []
    
    while graph: 
        all_nodes_have_inputs = set()
        all_nodes_have_outputs = set()
        
        for have_output_node, have_inputs in graph.items():
            all_nodes_have_outputs.add(have_output_node)#包括只有输出的节点 和既有输入又有输出的点
            all_nodes_have_inputs |= set(have_inputs) #有输入的点：包括既有输入和输出的点 和只有输入的点（末尾终点）
        need_removed_nodes = all_nodes_have_outputs - all_nodes_have_inputs #减去之后留下只有输出的节点
        
        if need_removed_nodes:
            node = random.choice(list(need_removed_nodes))  #随机删去一个节点
            visited_next = [node]
            
            if len(graph) == 1: visited_next += graph[node] #当最后删到只留一个有输出的节点
                #的时候，那么需要把这个节点对应的输出节点也加上，否则会漏掉这个点
                
            graph.pop(node)
            sorted_graph_nodes += visited_next
            
            for _, links in graph.items():
                if node in links: links.remove(node) #如果删除的节点在别的节点的连接关系内，那么把他从连接关系里删除
        else:
            break
            
    return sorted_graph_nodes
    
"""
根据feed_dict和网络节点的初始化结果,建立网络的连接关系
"""

from collections import defaultdict
def convert_feed_dict_graph(feed_dict):
    computing_graph = defaultdict(list)
    
    nodes = [n for n in feed_dict]
    
    while nodes:
        n = nodes.pop(0)  #移除列表中的一个元素（默认最后一个元素），并且返回该元素的值
        
    
        if isinstance(n,Placeholder):
            n.value = feed_dict[n]
        if n in computing_graph:continue
        
        for m in n.outputs:
            computing_graph[n].append(m) #建立好网络连接关系
            nodes.append(m)
            
    return computing_graph
   
   """
根据网络的连接关系，进行拓扑排序。
"""
def toplogical_sort(feed_dict):
    
    graph = convert_feed_dict_graph(feed_dict)
    
    return toplogical(graph)

实现正向传播和反向传播

#正向传播
def forward(graph,monitor=False,train = True):

  for node in graph if train else graph[:-1]:
      if monitor:print('forward:{}'.format(node))
      node.forward()
#反向传播
def backward(graph,monitor=False):
  
  for node in graph[::-1]:
      if monitor:print('backward:{}'.format(node))
      node.backward() 
     """
进行前向和反向传播计算
"""
"""
进行前向和反向传播计算
"""
def run_steps(graph_topological_sort_order,monitor=False,train=True):
  if train:
      forward(graph_topological_sort_order,monitor)
      backward(graph_topological_sort_order,monitor)
  else:
      forward(graph_topological_sort_order,monitor,train)

实现权值优化

def optimize(graph,learning_rate=1e-2):
 
 for node in graph:
     if node.is_trainable:
         node.value = node.value.reshape((node.value.shape[0],-1))
         node.gradients[node] = node.gradients[node].reshape((node.gradients[node].shape[0],-1))
         node.value += -1 * node.gradients[node] * learning_rate

定义保存模型和加载模型参数的函数

import os,zipfile
from glob import glob

def compress(zip_file, input_dir):
    f_zip = zipfile.ZipFile(zip_file, 'w')
    for root, dirs, files in os.walk(input_dir):
        for f in files:
             # 获取文件相对路径，在压缩包内建立相同的目录结构
            abs_path = os.path.join(os.path.join(root, f))
            rel_path = os.path.relpath(abs_path, os.path.dirname(input_dir))
            f_zip.write(abs_path, rel_path, zipfile.ZIP_STORED)

def extract(zip_file,pwd=None):
    if pwd:
        pwd = pwd.encode()
    f_zip = zipfile.ZipFile(zip_file, 'r')
    # 解压所有文件到指定目录
    f_zip.extractall(zip_file.split(".")[0],pwd=pwd)

    #return txt_file

import shutil
def save_model(save_path,model):

    save_path = save_path.split('.')[0]
    if not os.path.exists(save_path): #如果文件夹不存在，创建一个新的
        os.mkdir(save_path)

    for name, node in vars(model).items():
        if isinstance(node, Placeholder):
            if node.is_trainable:
                np.savetxt("{}/{}.txt".format(save_path,node.name), node.value)
    compress(os.getcwd() + '/{}.zip'.format(save_path), save_path, )
    shutil.rmtree(save_path)



def load_model(load_path,model):

    extract(load_path)
    load_path = load_path.split(".")[0]
    model_path = np.array(glob(load_path+"/*/*"))
    for name, node in vars(model).items():
        if isinstance(node, Placeholder):
            if node.is_trainable:
                for path in model_path:
                    if path.split(".")[0].split("/")[2] == node.name:
                        node.value = np.loadtxt(path)
    shutil.rmtree(load_path)

开始训练，与上节相比，我们输入了更多的特征。

from sklearn.datasets import load_boston
from tqdm import tqdm
from sklearn.utils import shuffle, resample
import numpy as np
import matplotlib.pyplot as plt


#加载数据
dataset = load_boston()
"""
print(dataset['feature_names'])
print(dataset['data'].shape)
print(dataset['target'].shape)
"""
x_ = dataset['data']
y_ = dataset['target']

# Normalize data
x_ = (x_ - np.mean(x_, axis=0)) / np.std(x_, axis=0)
# 定义网络
class MLP():
  def __init__(self,x_,y_):

      self.x, self.y = Placeholder(name='x', is_trainable=False), Placeholder(name='y', is_trainable=False)
      self.w1, self.b1 = Placeholder(name='w1'), Placeholder(name='b1')
      self.w2, self.b2 = Placeholder(name='w2'), Placeholder(name='b2')
      self.w3, self.b3 = Placeholder(name='w3'), Placeholder(name='b3')

      self.output1 = Linear(self.x, self.w1,self.b1, name='linear1')
      self.output2 = Sigmoid(self.output1, name='sigmoid')
      self.output3 = Linear(self.output2, self.w2, self.b2, name='linear2')
      self.output4 = ReLu(self.output3, name='Relu')
      self.y_pre = Linear(self.output4, self.w3, self.b3, name='linear3')
      self.MSE_loss = MSE(self.y_pre, self.y, name='MSE')

      hidden = 10
      hidden1 = 16
      output = 1
      #初始化数据结构
      self.feed_dict = {
          self.x: x_,
          self.y: y_,
          self.w1: np.random.rand(x_.shape[1], hidden),
          self.b1: np.zeros(hidden),
          self.w2: np.random.rand(hidden, hidden1),
          self.b2: np.zeros(hidden1),
          self.w3: np.random.rand(hidden1, output),
          self.b3: np.zeros(output),
}
batch_size = 16
mlp = MLP(x_,y_)
graph_sort = toplogical_sort(mlp.feed_dict)  #拓扑排序
m = x_.shape[0]
steps_per_epoch = m // batch_size
def train(model,epoch = 5000,learning_rate = 1e-3,steps_per_epoch=steps_per_epoch):
  #开始训练
  losses = []
  for e in range(epoch):
      loss = 0
      for b in range(steps_per_epoch):
          X_batch, y_batch = resample(x_, y_, n_samples=batch_size)
          mlp.x.value = X_batch  # 在这更新值
          mlp.y.value = y_batch
          # print(X_batch.shape)
          run_steps(graph_sort, monitor=False)

          optimize(graph_sort, learning_rate=learning_rate)

          loss += mlp.MSE_loss.value
      
      print("epoch:{},loss:{}".format(e, loss / steps_per_epoch))
      losses.append(loss / steps_per_epoch)
  #print("loss:{}".format(np.mean(losses)))
 
  save_model("mlp.zip",model)
  plt.plot(losses)
  plt.savefig("many_vectoy.png")
  plt.show()
train(mlp)

让我们可视化一下损失的变化过程

结果如下：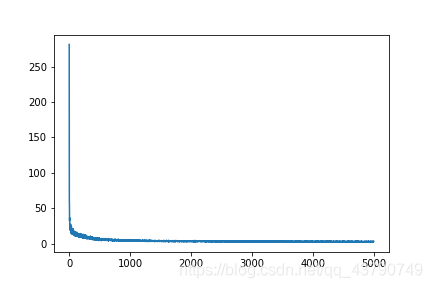

可以发现在多维特征的输入下，损失更小，预测的效果更佳。
预测：

load_model("mlp.zip",mlp)
def predict(x_rm, graph,model):
    model.x.value = x_rm
    run_steps(graph, monitor=False, train=False)

    return model.y_pre.value

print("预测值：",predict(x_[10],graph_sort,mlp),"真实值：",y_[10])
    #预测值： 18.52534730151933 真实值： 15.0

下一节我们将继续讲解将神经网络框架发布到pip官网的实现过程。