相关系数矩阵计算_相关系数简介及R计算

变量间Pearson、Spearman、Kendall、Polychoric、Tetrachoric、Polyserial、Biserial相关系数简介及R计算

对于给定数据集中，变量之间的关联程度以及关系的方向，常通过相关系数衡量。就关系的强度而言，相关系数的值在 +1 和 -1 之间变化，值 ±1 表示变量之间存在完美关联程度，即完全相关时绝对值为 1 ；随着相关系数值趋于 0 ，意味着变量之间的关系将减弱，完全不相关时为 0 。关系的方向由系数的符号表示； + 号表示正向关系， - 号表示负向关系。

图示两个变量之间的相关系数，正相关意味着图表从左到右具有向上的斜率：随着x值的增加，y值会变大；负相关性意味着图表从左到右具有向下的斜率：随着x值的增加，y值会变小；零(不相关)表示y不随x的变化而变化。

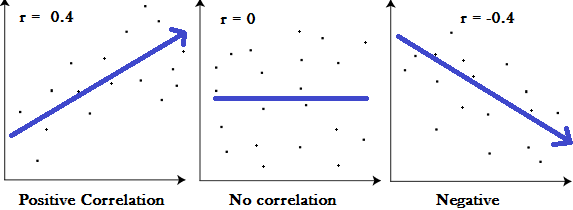
常见的变量间相关系数简介

首先简介常见的用于描述变量间相关性的系数，包括Pearson、Spearman、Kendall、Polychoric、Tetrachoric、Polyserial、(Point-)Biserial等。

Pearson相关(连续变量，数值相关)

Pearson相关系数(皮尔森相关)是使用最广泛的相关性统计量，用于测量两组连续变量之间的线性关联程度。

Pearson相关系数计算如下：

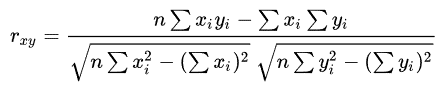
r_xy，变量x和y的Pearson相关系数；

n，观测对象的数量；

x_i，x的第i个观测值；

y_i，y的第i个观测值。

Pearson相关系数应用于连续变量，假定两组变量均为正态分布、存在线性关系且等方差。线性关系假设两个变量之间是线性响应的，等方差假设数据在回归线上均匀分布。

Spearman秩相关(连续变量，秩相关)

Spearman秩相关系数(斯皮尔曼等级相关)是一种非参数统计量，其值与两组相关变量的具体值无关，而仅仅与其值之间的大小关系有关。Spearman秩相关依据两列成对等级的各对等级数之差进行计算，所以又称为“等级差数法”。当变量在至少是有序的尺度上测量时，它是合适的相关分析方法。

Spearman秩相关系数计算如下：

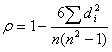
ρ，Spearman秩相关系数；

d_i，对应变量的秩之差，即两个变量分别排序后成对的变量位置(等级)差；

n，观测对象的数量。

Spearman秩相关同样应用于连续变量，与Pearson相关相比Spearman秩相关不要求变量的正态性和等方差假设，且对异常值的敏感度较低(该方法基于变量的排序，因此异常值的秩次通常不会有明显变化)，因此适用范围通常更广。但方法较为保守，统计效能较Pearson相关系数低，容易忽略一些不太强的线性关系。

此外，Spearman秩相关要求数据必须至少是有序的，一个变量的得分必须与另一个变量单调相关(monotonically related)。

Kendall相关(分类变量，秩相关)

Kendall 相关系数则用于计算分类变量间的秩相关，用于反映分类变量相关性的指标，适用于两个分类变量均为有序分类的情况。

考虑两组变量，x和y，它们各自的观测值数量均为n，则x与y观测值可能配对的总数为n(n-1)/ 2。由于x和y为分类变量，需要首先根据类别表示的重要度人工赋值。随后考察x和y的关系对，如果x_ii且x_jj，或x_i>y_i且x_j>y_j，则该关系对是一致的(concordant)，反正则不一致(discordant)。一致关系对数量与不一致关系对数量的差值除以总关系对数量，可得Kendall 相关系数：

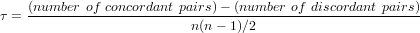
如果一致对的数量比不一致对的数量大得多，则变量是正相关的；如果一致对的数目比不一致对的数目少得多；则变量是负相关的；如果一致对的数目与不一致对的数目大致相同，则变量之间的关系很弱。

Polychoric相关(二元有序变量间的相关)

Polychoric相关(多分格相关)度量多个对象之间关于有序变量(有时称为“有序类别”数据)之间的一致性。当以列联表的形式组织数据时，两个分类自变量被排序，据此计算Polychoric相关系数。

对于2×2列联表的情况，Polychoric相关系数也称为Tetrachoric相关系数(作为Polychoric相关的一种常见类型)。通过以下对Tetrachoric相关的描述即可理解Polychoric相关的定义。

Tetrachoric相关(二元有序变量间的相关，Polychoric相关的某种常见类型)

Tetrachoric相关(四分相关)是在二元正态性假设下从2×2表推断出的Pearson相关，用于测量二元数据一致性。Tetrachoric相关要求基本变量来自正态分布，并且二元数据中存在一个潜在的连续梯度，即观测值的特征应该是连续而非离散的。

首先将观察数值矩阵获得列联表，并通过下式计算：

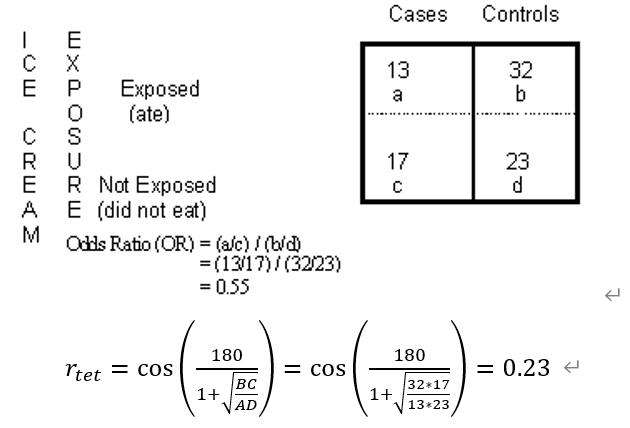
Polyserial相关(定量变量和序数变量的相关)

Polyserial相关(多系列相关)测量的是两个连续变量之间的相关关系，它们具有二元正态分布，其中一个变量可以直接观测到(以定量数值记录)，而另一个变量无法被观测(以序数值记录)。通过将可观测的连续变量分类为有限的离散有序值集，可以从可观测的有序变量获得不可观测有序变量的信息。

通过以下其特殊形式 Biserial 相关帮助理解。

Biserial相关(连续变量和二元有序变量的相关，Polyserial相关的某种特例)

Biserial相关系数为Polyserial相关的一种特例，用于测量一组连续变量和一组二元变量的线性关系，二元变量是二分序数类型，具有潜在的连续性。

Y₀，x=0时变量对的平均分；

Y₁，x=1时变量对的平均分；

p，x=1时变量对的比例；

q，x=0时变量对的比例；

σ_y，总体标准偏差。

Point-Biserial相关(连续变量和二元分类变量的相关)

与Biserial相关系数相比，Point-Biserial相关系数用于测量一组连续变量和一组二元分类变量的线性关系，分类变量是无序的。

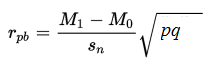
M₁，二元变量组“1”对象对应的连续变量的均值；

M₀，二元变量组“0”对象对应的连续变量的均值；

S_n，连续变量的标准偏差；

p，二元变量组“1”对象所占总对象的比例；

q，二元变量组“0”对象所占总对象的比例。

R语言计算相关系数

接下来展示在R中计算上述提到的相关系数的方法。

Pearson、Spearman和Kendall相关

在R中，cor()可用于计算Pearson、Spearman和Kendall相关矩阵，cov()可用于获得协方差矩阵。

##Pearson、Spearman、Kendall 相关
data(mtcars)
#标准化不影响相关系数计算值，但可以让数据服从均值 0，标准差 1 的等方差结构
mtcars  
#协方差计算，cov()
cov_pearson cov_pearson
cov_spearman cov_spearman
cov_kendall cov_kendall
#相关系数计算，cor()
cor_pearson cor_pearson
cor_spearman cor_spearman
cor_kendall cor_kendall
#相关图，例如
library(corrplot)
corrplot(cor_pearson, method = 'number', number.cex = 0.8, diag = FALSE, tl.cex = 0.8)
corrplot(cor_pearson, add = TRUE, type = 'upper', method = 'pie', diag = FALSE, tl.pos = 'n', cl.pos = 'n')
#输出，例如
write.table(cor_pearson, 'cor_pearson.txt', sep = '\t', col.names = NA, quote = FALSE)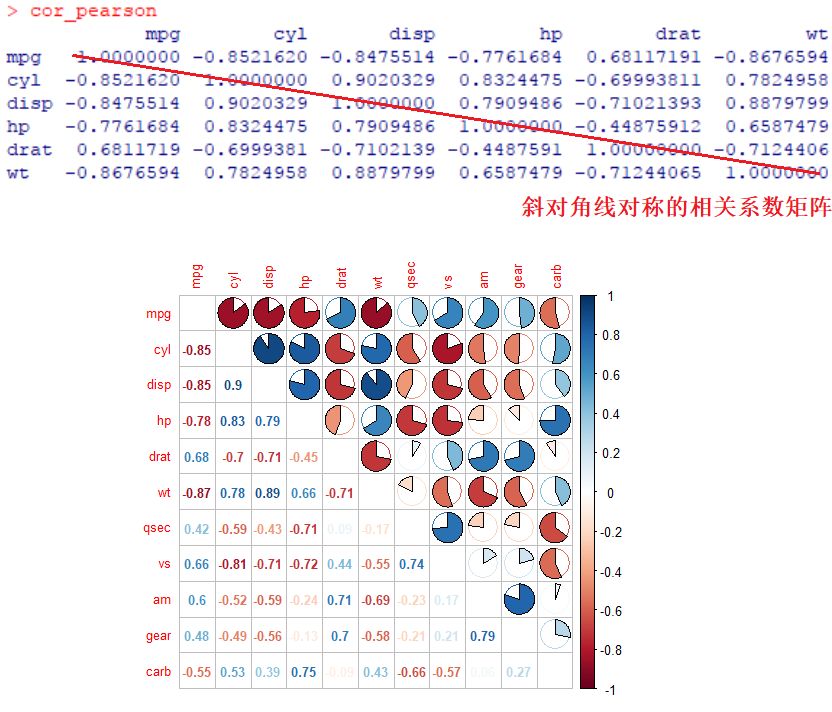

直接指定数据集，默认计算所有变量间的相关系数，获得斜对角线对称的矩阵。

也可指定两组变量集，获得相互之间两两变量间非对称的相关矩阵。

#指定两组变量集，获得非对称的相关矩阵，例如
x y  
cor_pearson_xy cor_pearson_xy
#相关图
corrplot(cor_pearson_xy, method = 'square', addCoef.col = 'black', number.cex = 0.8, tl.cex = 1.2)
#输出，例如
write.table(cor_pearson_xy, 'cor_pearson_xy.txt', sep = '\t', col.names = NA, quote = FALSE)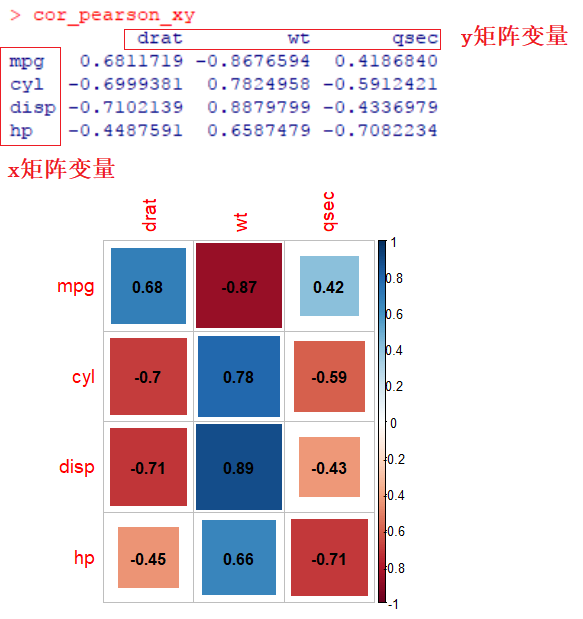

偏相关

偏相关是指在控制一个或多个定量变量时，另外两个定量变量之间的相互关系。R包ggm中提供的命令pcor()可以计算偏相关系数。

##偏相关，ggm 包 pcor()
library(ggm)
#要计算相关系数的两个变量，或指定下标
x1  
#要控制的条件变量，或指定下标
x2  
#指定协方差矩阵，计算偏相关
pcor_pearson pcor_pearson

Polychoric和Tetrachoric相关

psych包提供了计算这些相关系数的方法。

psych包也能计算Polyserial和Biserial相关，但文档中没提供示例，没看明白……

##Polychoric、Tetrachoric
library(psych)
#Polychoric 相关
data(bock)
polyc polyc
#Tetrachoric 相关
tetr tetr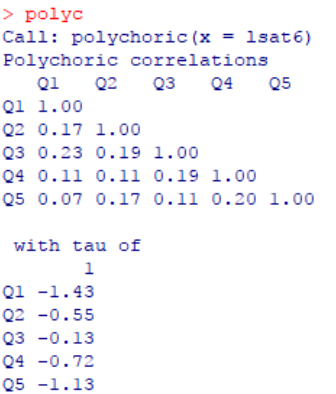

Polyserial和(Point-)Biserial相关

以ltm包提供的方法为例。

##Polyserial、(Point-)Biserial
library(ltm)
#Polyserial 相关
mpg polys polys
#Point-Biserial 相关
poi_biser poi_biser
#Biserial 相关
biser biser

变量相关性的显著性检验

通常来讲，相关性分析是一种用于描述变量关联程度的探索性分析方法，而非确立因果关系的模型，不涉及假设检验过程。但如果有必要，仍可以计算相关系数的显著性，评估哪些变量间的关联程度是更重要的。

一些R包提供了计算变量间相关系数显著性的方法。此外，也可以自写函数获得，见下文。

psych包的方法

计算相关矩阵及显著性水平。

library(psych)
#所有变量间相关系数的对称矩阵
corr_matrix corr_matrix$r    #相关矩阵
corr_matrix$p    #p 值矩阵
#相关图，只展示 p < 0.05 的相关系数
library(corrplot)
col1 corrplot(corr_matrix$r, p.mat = corr_matrix$p, sig.level = 0.05, insig = 'blank', method = 'number',
     diag = FALSE, col = col1(21), tl.cex = 1)
corrplot(corr_matrix$r, p.mat = corr_matrix$p, sig.level = 0.05, insig = 'blank', method = 'circle',
    add = TRUE, type = 'upper', diag = FALSE, col = col1(21), tl.pos = 'n', cl.pos = 'n')
#自定义筛选，例如选择 |r| >=0.7，p < 0.05 的结果，将不满足条件的相关系数值赋值为 0 后输出
corr_matrix$p[corr_matrix$p >= 0.05] corr_matrix$p[corr_matrix$p < 0.05 & corr_matrix$p >= 0] corr_matrix$p[corr_matrix$p == -1]  
corr_matrix$r[abs(corr_matrix$r) < 0.7] corr_matrix$r write.table(corr_matrix$r, 'corr_matrix_select.txt', sep = '\t', col.names = NA, quote = FALSE)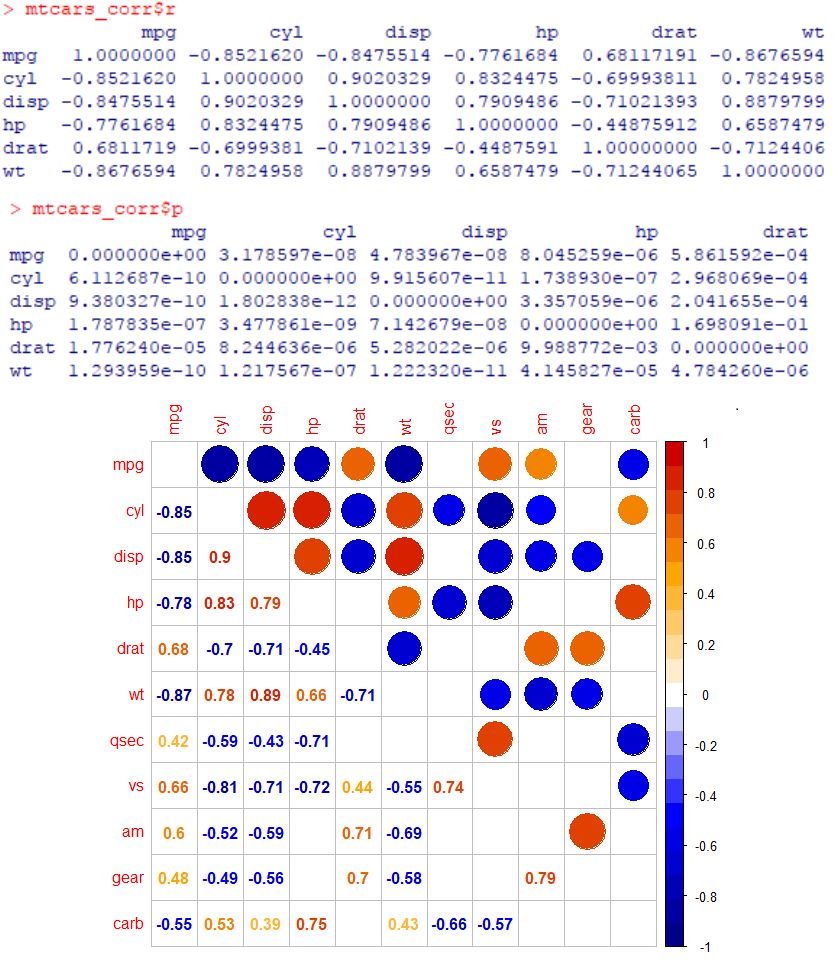

#给定两组变量间相关系数的非对称矩阵
x y  
corr_matrix corr_matrix$r    #相关矩阵
corr_matrix$p    #p 值矩阵
#相关图，只展示 p < 0.05 的相关系数
col1 corrplot(corr_matrix$r, p.mat = corr_matrix$p, sig.level = 0.05, insig = 'blank',
    method = 'square', addCoef.col = 'black', col = col1(21), number.cex = 0.8, tl.cex = 1.2)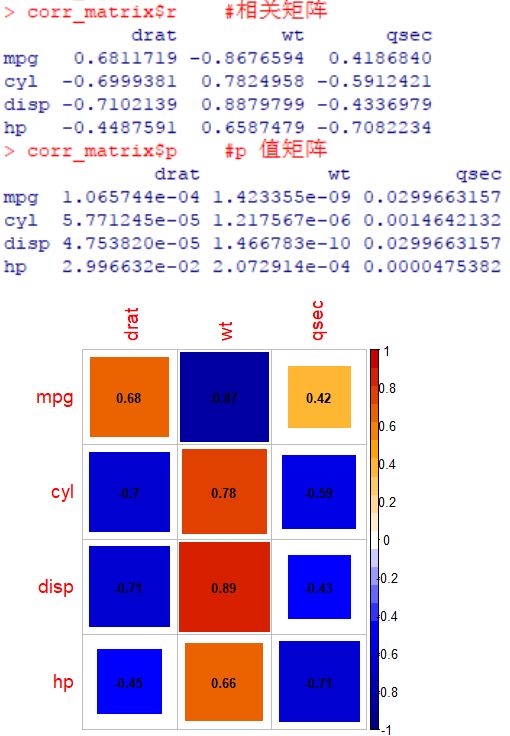

Hmisc包的方法

计算相关矩阵及显著性水平。

library(Hmisc)
#所有变量间相关系数的对称矩阵
rcorr_matrix rcorr_matrix$r    #相关矩阵
rcorr_matrix$P    #p 值矩阵
#给定两组变量间相关系数的非对称矩阵
x y  
rcorr_matrix rcorr_matrix$r    #相关矩阵
rcorr_matrix$P    #p 值矩阵
#相关图、自定义结果筛选等，参考上述

手写置换检验程序

置换检验是个百搭的非参数检验方法，相关系数的显著性可根据置换检验的原理获得。

上述提到的所有相关系数，包括Polychoric、Tetrachoric、Polyserial、(Point-)Biserial等，如果找不到计算显著性的R包，不妨考虑手写函数计算，其实并不难。

#计算观测值的相关系数(cor0)，还是以 Pearson 相关为例，其它类似
cor0  
#随机置换数据 999 次，计算每次置换后数据计算的相关系数(corN)，并统计 |corN|>|cor0| 的频数
p_num p_num[abs(p_num)>0]  
set.seed(123)
for (i in 1:999) {
    random     corN     
    corN[abs(corN) >= abs(cor0)]     corN[abs(corN) < abs(cor0)]     p_num }
#p 值矩阵，即 |corN|>|cor0| 的概率
p p
#相关图比较，仅显著(p < 0.05)的相关系数标以背景色
#左图为手写的置换检验结果，右图为 psych 包获得的结果，二者是一致的
library(corrplot)
library(psych)
cor_psych  
layout(matrix(c(1,2), 1, 2, byrow = TRUE))
corrplot(cor0, method = 'square', type = 'lower', p.mat = p, sig.level = 0.05, insig = 'blank',
    addCoef.col = 'black', diag = FALSE, number.cex = 0.8, tl.cex = 0.8)
corrplot(cor_psych$r, method = 'square', type = 'lower', p.mat = cor_psych$p, sig.level = 0.05, insig = 'blank',
    addCoef.col = 'black', diag = FALSE, number.cex = 0.8, tl.cex = 0.8)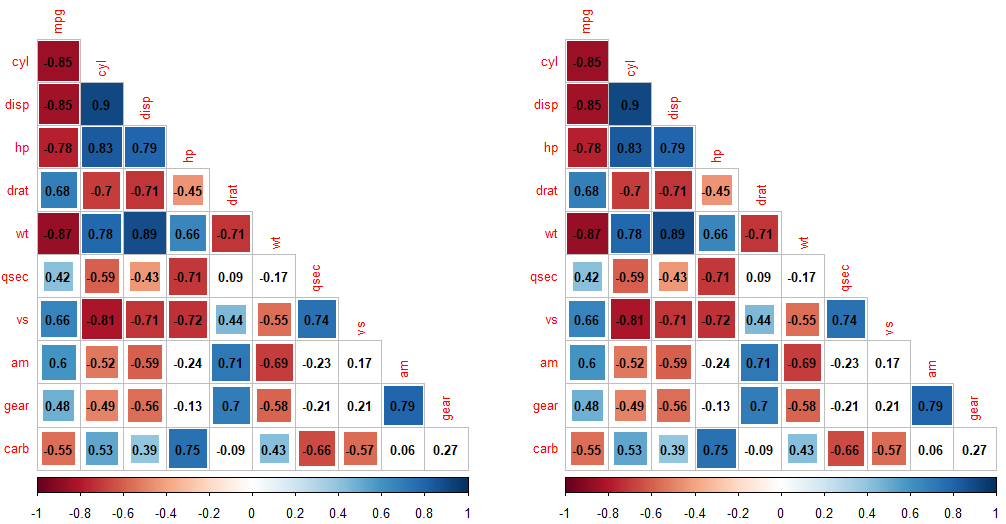

参考资料

Pearson, Spearman & Kendall：https://www.statisticssolutions.com/correlation-pearson-kendall-spearman/

(Point-)Biserial：https://www.statisticshowto.datasciencecentral.com/point-biserial-correlation/

Tetrachoric & Polychoric：http://john-uebersax.com/stat/tetra.htm

Polyserial：http://support.sas.com/documentation/cdl/en/procstat/63963/HTML/default/viewer.htm#procstat_corr_sect019.htm

友情链接