2.1 数值与编码
主要分为BCD,海明码,奇偶校验,CRC四种校验码,总结一下。
一、BCD码
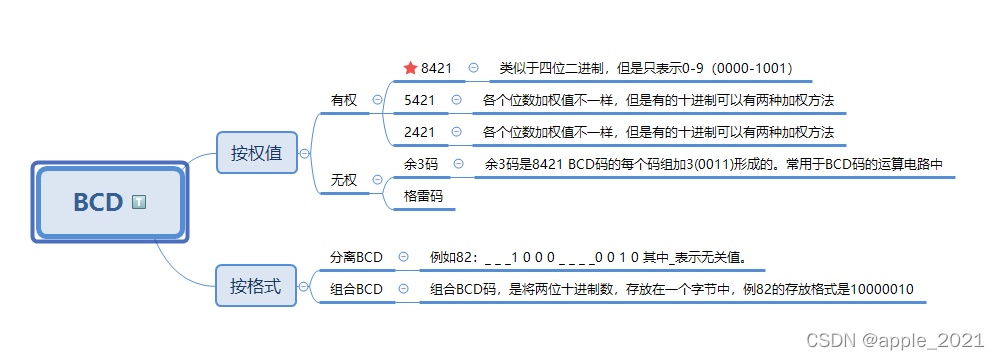
最常见的BCD码就是 8421码,它与二进制相似,各个位数的权值分别为8,4,2,1。
1、8421码的表示
(1)十进制数:123
对应的8421码为:0001 0010 0011
(2)8421码:0011 0010 0001
对应的十进制数为:321
2、8421码的进位
因为8421码中的9为1001,10为0001 0000,可见8421码遇见1001就产生进位。而普通的二进制码,到1111才产生进位10000。
二、奇偶校验码
主要用于检测数据传输中是否发生错误,顾名思义分为奇校验和偶校验,是众多校验码中最为简单的一种。
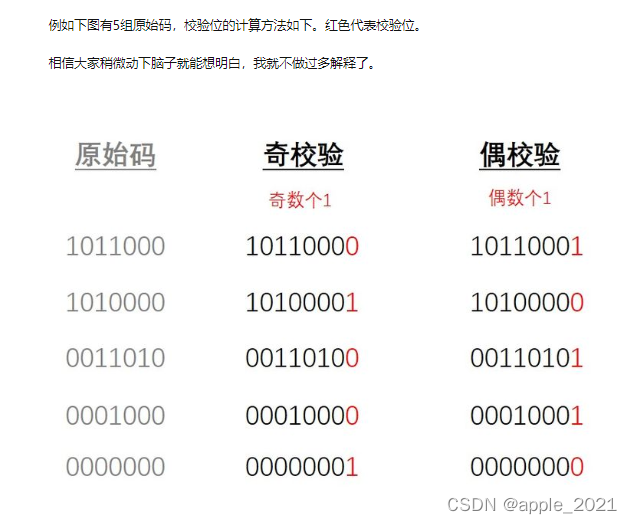
奇校验:数据位 + 校验位 总共有奇数个1
偶校验:数据位 + 校验位 总共有偶数个1
校验位只有一位,0或者1,可放数据位前或后;
三、海明码
步骤:
- 确定校验位数 k ,n是信息码的位数,公式为:2^k ≥ k+n+1
- 确定校验位在海明码中的位置 ( 2^k 都是校验位)
- 推算每个校验位是0还是1
具体操作不太好描述,直接上例题
例如:给定一组信息码:110001,求其海明码
第一步:确定校验位数 k
110001为信息码,有六位,则n = 6,套公式 2^k ≥ k + 6 + 1 推出 k = 4
第二步:确定校验位在海明码中的位置
记住2^k 就是校验码的位置,即1、2、4、8 的位置。
| 位置 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 海明码 | 1 | 1 | H8 | 0 | 0 | 0 | H4 | 1 | H2 | H1 |
第三步:推算每个校验位是0还是1(重点)
将位置变为二进制
| 位置 | 10 (1010) | 9 (1001) | 8 (1000) | 7 (0111) | 6 (0110) | 5 (0101) | 4 (0100) | 3 (0011) | 2 (0010) | 1 (0001) |
|---|---|---|---|---|---|---|---|---|---|---|
| 海明码 | 1 | 1 | H8 | 0 | 0 | 0 | H4 | 1 | H2 | H1 |
分析能校验 信息码的哪些位置 比如1(***1),可校验最后一位为1的位置,即3、5、7、9位置上的信息码
目前校验位为
1:×××1,可校验 3、5、7、9
2:××1×,可校验 3、6、7、10
4:×1××,可校验 5、6、7
8:1×××,可校验 9、10
因为海明码基本上都是偶校验(偶数个1),根据各个位置上的信息异或计算出校验码
H1 ^ 1 ^ 0 ^ 0 ^ 1 要满足偶校验 推出H1 = 0,同理可得H2、H4、H8位置所对应的校验码
最后,海明码为 11 0000 0100
- 海明码只能检测出2位错,纠1位错
- 海明码默认进行偶校验
四、循环冗余码(CRC)
CRC中校验位在信息位后面,先确定校验码有几位,然后进行模二除法(异或),余数即为校验码;
以一个题目为例:
设待校验的数据为。信息位:10101011,若采用CRC,且生成多项式为 10011(也可写成:G(x) = x^4 + x + 1),则其 CRC 码为?
- 先根据多项式计算校验码的位数
若为10011,则校验码位数为总位数-1,即R = 5-1=4
若为x^4 + x + 1,则最高次幂即为校验码位数R = 4 - 信息码左移R位,低位补零。
10101011 0000 - 计算校验码(模二,异或),则余数为校验位
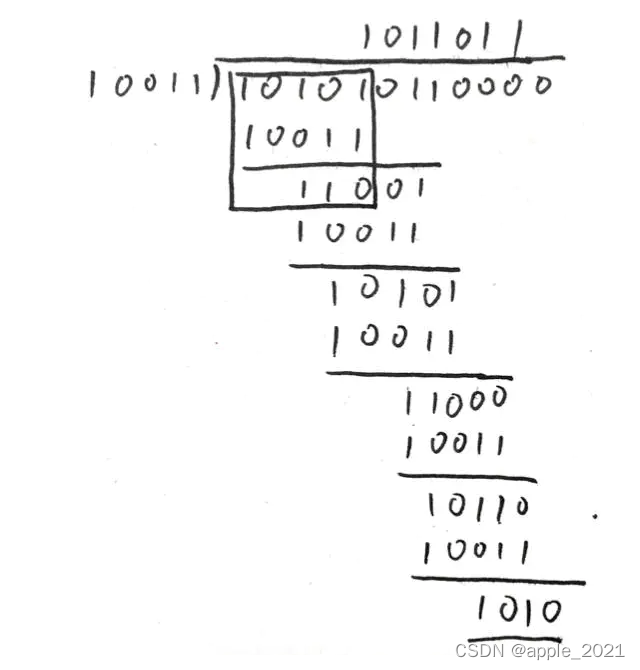
最后得到的余数:1010,即是校验位。那么整个CRC码为:10101011 1010 - 检验,对该数除多项式(10011),若能整除(余数为0)则正确,否则需要重传或者纠错;
假设收到的CRC码变成了10001011 1010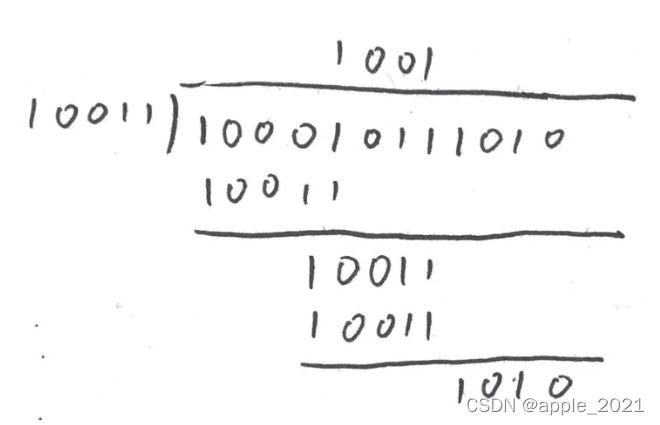
余数为1010,则不正确;