RepVGG将训练推理网络结构进行独立设计,在训练时使用高精度的多分支网络学习权值,在推理时使用低延迟的单分支网络,然后通过结构重参数化将多分支网络的权值转移到单分支网络。RepVGG性能达到了SOTA,思路简单新颖,相信可以在上面做更多的工作来获得更好的性能。
来源:晓飞的算法工程笔记 公众号
论文: RepVGG: Making VGG-style ConvNets Great Again

Introduction
目前,卷积网络的研究主要集中在结构的设计。复杂的结构尽管能带来更高的准确率,但也会带来推理速度的减慢。影响推理速度的因素有很多,计算量FLOPs往往不能准确地代表模型的实际速度,计算量较低的模型不一定计算更快。因此,VGG和ResNet依然在很多应用中得到重用。
基于上述背景,论文提出了VGG风格的单分支网络结构RepVGG,能够比结构复杂的多分支网络更优秀,主要包含以下特点:
- 模型跟VGG类似,不包含任何分支,无需保存过多的中间结果,内存占用少。
- 模型仅包含3 × 3 3\times 33×3卷积和ReLU,计算速度快。
- 具体的网络结构(包括深度和宽度)不需要依靠自动搜索、人工调整以及复合缩放等复杂手段进行设计,十分灵活。
当然,想要直接训练简单的单分支网络来达到与多分支网络一样的精度是很难的。由于多分支网络中的各个分支在训练时的权重变化不定,所以多分支网络可看作是大量简单网络的合集,而且其能够避免训练时的梯度弥散问题。虽然如此,但多分支网络会损害速度,所以论文打算训练时采用多分支网络,而推理时仍然使用单分支网络,通过新颖的结构性重参数化(structural re-parameterization)将多分支网络的权值转移到简单网络中。
Building RepVGG via Structural Re-param
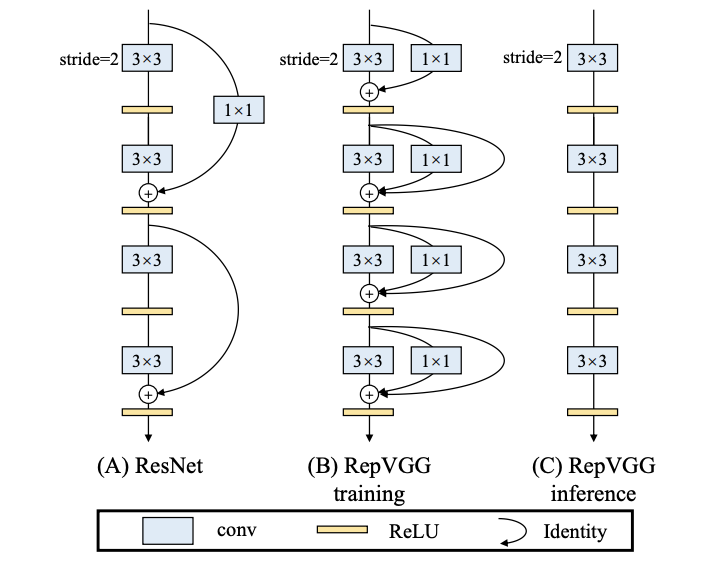
Training-time Multi-branch Architecture
由于多分支的存在,使得多分支网络相当于一个包含大量小网络的集合,但其推理速度会有较大影响,所以论文仅在训练时使用多分支进行训练,训练完成后将其权值转移到简单网络中。为了够包含大量更简单的模型,论文在3 × 3 3\times 33×3卷积的基础上添加ResNet-like的identity分支和1 × 1 1\times 11×1分支构成building block,然后堆叠成训练模型。假设多分支网络包含n nn个building block,则其可以表达3 n 3^n3n种简单网络结构。
Re-param for Plain Inference-time Model
在开始描述最重要的权值转换之前,先进行以下定义:
- 定义3 × 3 3\times 33×3卷积为W ( 3 ) ∈ R C 2 × C 1 × 3 × 3 W^{(3)}\in \mathbb{R}^{C_2\times C_1\times 3\times 3}W(3)∈RC2×C1×3×3,1 × 1 1\times 11×1卷积为W ( 1 ) ∈ R C 2 × C 1 W^{(1)}\in \mathbb{R}^{C_2\times C_1}W(1)∈RC2×C1。
- 定义μ ( 3 ) \mu^{(3)}μ(3)、σ ( 3 ) \sigma^{(3)}σ(3)、γ ( 3 ) \gamma^{(3)}γ(3)和β ( 3 ) \beta^{(3)}β(3)为跟在3 × 3 3\times 33×3卷积后面的BN层的累计均值、标准差、学习到的缩放因子和偏置,跟在1 × 1 1\times 11×1卷积后面的BN层的参数为μ ( 1 ) \mu^{(1)}μ(1)、σ ( 1 ) \sigma^{(1)}σ(1)、γ ( 1 ) \gamma^{(1)}γ(1)和β ( 1 ) \beta^{(1)}β(1),跟在identity分支后面的BN层参数为μ ( 0 ) \mu^{(0)}μ(0)、σ ( 0 ) \sigma^{(0)}σ(0)、γ ( 0 ) \gamma^{(0)}γ(0)和β ( 0 ) \beta^{(0)}β(0)。
- 定义输入为M ( 1 ) ∈ R N × C 1 × H 1 × W 1 M^{(1)}\in \mathbb{R}^{N\times C_1\times H_1\times W_1}M(1)∈RN×C1×H1×W1,输出为M ( 2 ) ∈ R N × C c × H 2 × W 2 M^{(2)}\in \mathbb{R}^{N\times C_c\times H_2\times W_2}M(2)∈RN×Cc×H2×W2。
- 定义∗ *∗为卷积操作。
假设C 1 = C 2 C_1=C_2C1=C2、H 1 = H 2 H_1=H_2H1=H2以及W 1 = W 2 W_1=W_2W1=W2,则有:

若输入输出维度不相同,则去掉identity分支,即只包含前面两项。b n bnbn代表是推理时的BN函数,一般而言,对于∀ 1 ≤ i ≤ C 2 \forall 1\leq i \leq C_2∀1≤i≤C2,有:

权值转换的核心是将BN和其前面的卷积层转换成单个包含偏置向量的卷积层。假设{ W ′ , b ′ } \{W^{'}, b^{'}\}{W′,b′}为从{ W , μ , σ , γ , β } \{W, \mu, \sigma, \gamma, \beta\}{W,μ,σ,γ,β}转换得到的核权值和偏置,则有:

转换后的卷积操作与原本的卷积+BN操作是等价的,即:

上述的转换也可应用于identity分支,将identity mapping视作卷积核为单位矩阵的1 × 1 1\times 11×1卷积。

以上图为例,在C 2 = C 1 = 2 C_2=C_1=2C2=C1=2的情况下,将3个分支分别转换后得到1个3 × 3 3\times 33×3卷积和两个1 × 1 1\times 11×1卷积,最终的卷积偏置由3个卷积的偏置直接相加,而最终的卷积核则是将两个1 × 1 1\times 11×1卷积核加到3 × 3 3\times 33×3卷积核中心。需要注意的是,为了达到转换的目的,训练时的3 × 3 3\times 33×3卷积分支和1 × 1 1\times 11×1卷积分支需要有相同的步长,而1 × 1 1\times 11×1卷积的填充要比3 × 3 3\times 33×3卷积的小一个像素。
Architectural Specification

RepVGG是VGG风格的网络,主要依赖3 × 3 3\times 33×3卷积,但没有使用最大池化,而是使用步长为2的3 × 3 3\times 33×3卷积作为替换。RepVGG共包含5个阶段,每个阶段的首个卷积的步长为2。对于分类任务,使用最大池化和全连接层作为head,而其它任务则使用对应的head。

每个阶段的层数的设计如上表所示,除首尾两个阶段使用单层外,每个阶段的层数逐渐增加。而每个阶段的宽度则通过缩放因子a aa和b bb进行调整,通常b > a b \gt ab>a,保证最后一个阶段能够提取更丰富的特征。为了避免第一阶段采用过大的卷积,进行了m i n ( 64 , 64 a ) min(64, 64a)min(64,64a)的设置。
为了进一步压缩参数,论文直接在特定的层加入分组卷积,从而达到速度和准确率之间的trade-off,比如RepVGG-A的3rd, 5th, 7th, …, 21st层以及RepVGG-B的23rd, 25th和27th层。需要注意,这里没有对连续的层使用分组卷积,主要为了保证通道间的信息交流。
Experiment


SOTA分类在120epoch训练的性能对比。

200epoch带数据增强的分类性能对比。

对比多分支效果。

其它操作与结构重参数化的对比实验。

作为分割任务的主干网络的表现。
Conclusion
RepVGG将训练推理网络结构进行独立设计,在训练时使用高精度的多分支网络学习权值,在推理时使用低延迟的单分支网络,然后通过结构重参数化将多分支网络的权值转移到单分支网络。RepVGG性能达到了SOTA,思路简单新颖,相信可以在上面做更多的工作来获得更好的性能。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】
