基于小波变换的图像去噪
前言
信号的产生、处理及传输都不可避免地要受到噪声的干扰,此外,由于有限字长影响,在数字信号处理中又普遍地存在着模拟信号抽样时的量化噪声和计算时的舍入噪声,因此去噪是信号处理中的永恒的话题。信号处理中的许多理论都和去噪紧密相关,如滤波器设计、最优估计、奇异值分解(SVD)、独立分量分析(ICA)、相干平均以及信号建模等。
传统的滤波方法是假定信号和噪声处在不同的频带,但实际上噪声(特别是作为噪声模型的白噪声)的频带往往分布在整个频率轴上,且等幅度,因此,滤波的方法有其局限性。上述方法尽管在某些方面有自己的特点,但作为信号处理中的去噪问题,其理论和方法都还远远没有解决。
正交小波变换是通过 Mallat的多分辨率分解来实现的H0(z)。通过低通滤波器H0(z)和高通滤波器H1(z)将信号的频谱分解到不同的频率范围,从而得到一个个的子带信号;又由于正交变换具有去除信号中的相关性和信号能量集中的功能,因此,通过小波变换就把信号的能量集中到某些频带的少数系数上这样,通过将其他频带上的小波系数置零或是给予小的权重,即可达到有效抑制噪声的目的。因此,小波去噪随着小波变换理论的发展也不断丰富起来,并取得了良好的效果。其中,以 Donoho的阈值去噪法最为突出,本文的小波去噪法即为阈值去噪法。
提示:以下是本篇文章正文内容,下面案例可供完整代码参考如下:
链接:https://pan.baidu.com/s/1gOiCBfkVrNwDJj8SfhOaLQ
提取码:qmwz
一、小波变换的发展
传统的信号理论,是建立在Fourier分析基础上的,而Fourier变换作为一种全局性的变化,有一定的局限性,如不具备局部化分析能力、不能分析非平稳信号等。在实际应用中人们开始对Fourier变换进行各种改进,以改善这种局限性,如STFT(短时傅立叶变换)。由于STFT采用的的滑动窗函数一经选定就固定不变,故决定了其时频分辨率固定不变,不具备自适应能力,而小波分析很好的解决了这个问题。小波变换(wavelet transform,WT)是一种新的变换分析方法,它继承和发展了短时傅立叶变换局部化的思想,同时又克服了窗口大小不随频率变化等缺点,能够提供一个随频率改变的“时间-频率”窗口,是进行信号时频分析和处理的理想工具。它的主要特点是通过变换能够充分突出问题某些方面的特征,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。
二、阈值去噪法的介绍
2.1. 基本原理
小波阈值去噪的基本思想是先设置一个临界阈值λ,若小波系数小于λ,认为该系数主要由噪声引起,去除这部分系数;若小波系数大于λ,则认为此系数主要是由信号引起,保留这部分系数,然后对处理后的小波系数进行小波逆变换得到去噪后的信号。
2.2. 流程图

2.3. 阈值函数的选取
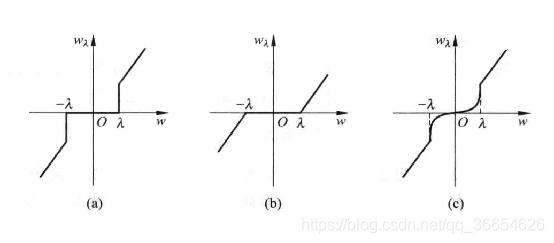
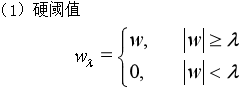
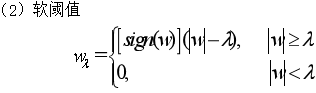
硬阈值是一种简单的置零的方法,而软阈值对于大于阈值的小波系数作了"收缩",即都减去阈值,从而使输入-输出曲线变成连续的。在阈值选选取上,人们普遍使用软阈值。改进的阈值是硬阈值和软阈值之间的一个折中,即当小波系数小于阈值时,不是简单地置为零,而是平滑地减小为零,当大于阈值时,小波系数幅度都减去阈值。这样,既保证了大的小波系数,又保证了加阈值后系数的平滑过渡。
本次设计自定义了一个折中阈值,当小波系数等于阈值时,在阈值上加了一个折中系数α,实现阈值从硬阈值到软阈值的平缓过渡。折中系数的范围是0-100,即α=0时为硬阈值,α=100时为软阈值,α在0到100的范围之间为折中阈值。
2.4. 阈值的选取
小波阈值选取方法有固定阈值(Sqtwolog阈值),风险阈值(Rigrsure阈值),启发式阈值(Heursure阈值),极大极小阈值。这些阈值选取方法中都没有涉及噪声的方差,这与我们的实验理念相违背,在MATLAB中我们对噪声方差进行了单独的处理。取小波系数在各个尺度下绝对值的中值,然后将该中值除以常数0.6745作为该尺度下小波系数中噪声强度的估计,即
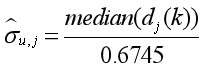
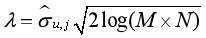
2.5. 分解函数和重构函数
在MARTLAB中,wavedec2()可以实现图像的多级分解,其格式为
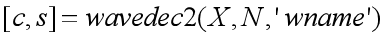
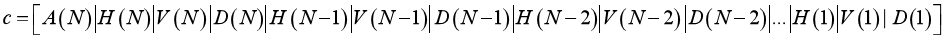

2.6. 峰值信噪比(PSNR)
峰值信噪比经常用作图像压缩和去噪等领域中信号重建质量的测量方法,它常简单地通过均方差(MSE)进行定义。两个m×n单色图像I和K,如果一个为另外一个的噪声近似,那么它们的的均方差定义为
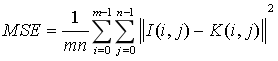
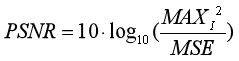
2.7. 实验参数的设计
该设计是在MATLAB2018b环境下编程实现的,经过多次的仿真,我们所选的噪声参数为:均值为0,方差0.02、0.04以及0.06的高斯白噪声。阈值函数用了硬阈值、软阈值和改进的阈值三种方法,阈值选取方式为全局阈值。小波基为db2,它是dbN小波的一种,小波分解级数为3级。所用的图片是自己拍摄的博物馆图片,大小为512x512的灰度图。
三、部分代码
3.1. 主函数
代码如下(main.c):
lc,clf,clear
%输入一幅图像
image=imread('Photo.bmp');
%加入不同程度的高斯噪声
image1= imnoise(image, 'gaussian', 0,0.02);
image2= imnoise(image, 'gaussian', 0,0.04);
image3= imnoise(image, 'gaussian', 0,0.06);
figure('NumberTitle', 'off', 'Name', '原图像和噪声图像')
subplot(221);imshow(image);title('原图像');
subplot(222);imshow(image1);title('均值为0,方差为0.02的噪声图像');
subplot(223);imshow(image2);title('均值为0,方差为0.04的噪声图像');
subplot(224);imshow(image3);title('均值为0,方差为0.06的噪声图像');
disp('0.02噪声图像的峰值信噪比:'),psnr(image,image1)
disp('0.04噪声图像的峰值信噪比:'),psnr(image,image2)
disp('0.06噪声图像的峰值信噪比:'),psnr(image,image3)
test_num=randi([1,99],1,1);%随机生成一个数作为折中系数
wname='db2';n=3;input=image1;
subplot(221);
[img1,psn1]=WaveletDenoising(input,n,wname,image,0);
imshow(img1,[]);title('硬阈值去噪后的图像'),
disp('硬阈值去噪后的峰值去噪比:'),psn1
subplot(222);
[img2,psn2]=WaveletDenoising(input,n,wname,image,100);
imshow(img2,[]);title('软阈值去噪后的图像'),
disp('软阈值去噪后的峰值去噪比:'),psn2
subplot(223);
[img3,psn3]=WaveletDenoising(input,n,wname,image,test_num);
imshow(img3,[]);title('随机折中系数去噪后的图像'),
disp('随机折中系数去噪后的峰值去噪比:'),psn3
subplot(224);
[img4,psn4]=WaveletDenoising(input,n,wname,image,-1);
imshow(img4,[]);title('最佳折中系数去噪后的图像'),
disp('最佳折中系数去噪后的峰值去噪比:'),psn4
3.2. 阈值去噪函数
代码如下(WaveletDenoising.m):
function [Image,Psnr]=WaveletDenoising(x,n,wname,image,a)
%函数功能:
% y=WaveletDenoising(x,n,wname)
% 选择一副图像,加上不同程度的高斯噪声,对带噪图像进行小波分解,
% 对小波系数进行阈值处理再利用处理后的结果重构原图像
%输入参数:
% x----输入的噪声图像
% n----小波分解的层数
% wname----小波基函数
% a----折中系数
%输出参数:
% Image----原图像去噪后重构的图像
% Sndz----峰值信噪比
[c,s]=wavedec2(x,n,wname); %进行3层小波分解
for i=1:3 %获取各层各高频分量在c向量中的坐标
if i==1
num(i,1)=s(i,1)*s(i,2)+1;
num(i,2)=num(i,1)+s(i+1,1)*s(i+1,2);
num(i,3)=num(i,2)+s(i+1,1)*s(i+1,2);
step(i)=s(i+1,1)*s(i+1,2);
else
num(i,1)=num(i-1,3)+s(i,1)*s(i,2);
num(i,2)=num(i,1)+s(i+1,1)*s(i+1,2);
num(i,3)=num(i,2)+s(i+1,1)*s(i+1,2);
step(i)=s(i+1,1)*s(i+1,2);
end
end
C=c;
for j=1:101
b(j)=0.01*(j-1); %折中系数取0到1中的两位小数进行比较
for i=1:3
[H,V,D]=detcoef2('a',c,s,i); %提取第i层各高频系数
B=[H V D];
[M,N]=size(B);
for k=1:M
for w=1:N
sigma=median(abs(B(k,w)))/0.6745;%噪声方差
end
end
th=sigma*sqrt(2*log10(M*N));
ch=c(1,num(4-i,1):num(4-i,2)+step(4-i)-1);%对各高频系数进行阈值处理
C(1,num(4-i,1):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(ch,th,b(j));%阈值处理函数
cv=c(1,num(4-i,2):num(4-i,2)+step(4-i)-1);
C(1,num(4-i,2):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(cv,th,b(j));
cd=c(1,num(4-i,3):num(4-i,2)+step(4-i)-1);
C(1,num(4-i,3):num(4-i,2)+step(4-i)-1)=ThresholdProcessing(cd,th,b(j));
end
ReImage(:,:,j)=waverec2(C,s,wname);%重构图像
[a1,b1]=size(image);%计算峰值信噪比
sqr=double(image) - double(ReImage(:,:,j));
mse= sum(sum( sqr.^2 ))/(a1*b1);
PSNR(j)= 10*log10( 255*255 / mse );
end
%返回输出值
a=a+1;
[Ma,Mn]=max(PSNR);
if a==0
Psnr=Ma;
Image=ReImage(:,:,b(Mn)*100);
else
Image=ReImage(:,:,a);
Psnr=PSNR(a);
end
end
3.3. 阈值处理函数
代码如下(ThresholdProcessing.m):
function y = ThresholdProcessing(A,t,a )
%阈值处理函数
% A为待处理量,t为阈值,a为折中系数
tmp=abs(A)-a*t;
tnp=abs(A)>=t;
y=(sign(A).*tmp).*tnp;
end
3.4. 峰值信噪比
代码如下(psnr.m):
function PSNR = psnr(image1,image2 )
% 计算峰值信噪比
% image1是原图像
% image2是去噪后的图像
[a,b]=size(image1);
sqr=double(image1) - double(image2);
mse= sum(sum( sqr.^2 ))/(a*b);
PSNR= 10*log10( 255*255 / mse );
end
3.5. 折中系数函数
代码如下(main_test.c):
clc,clf,clear
%输入一幅图像
image=imread('Miss.bmp');
% image=rgb2gray(image);
%加入不同程度的高斯噪声
image1= imnoise(image, 'gaussian', 0,0.01);
image2= imnoise(image, 'gaussian', 0,0.02);
image3= imnoise(image, 'gaussian', 0,0.04);
figure(1)
psdn=[]
x=0:100;
for i=0:100
if i==0
[img,psn]=WaveletDenoising(image1,3,'db2',image,0);
psdn=[psdn,psn];
elseif(i==100)
[img,psn]=WaveletDenoising(image1,3,'db2',image,100);
psdn=[psdn,psn];
else
[img,psn]=WaveletDenoising(image1,3,'db2',image,i);
psdn=[psdn,psn];
end
plot(psdn);
disp('迭代次数:'),i
end
xlabel('迭代次数');ylabel('峰值信噪比PSNR');
title('噪声方差0.02,PSNR随折中系数的变化');
四、实验结果
4.1 结果图



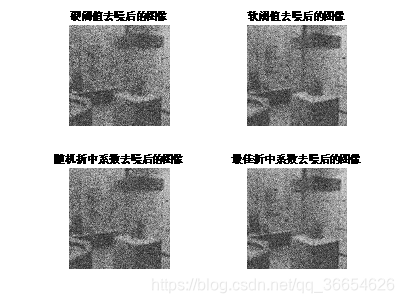
由上图可以看出,我们加了不同程度的高斯噪声,均值都为0,方差分别为0.02、0.04和0.06,经过小波的阈值去噪,图像的清晰度得到了明显的提高。同时比较硬阈值、软阈值以及最佳折中阈值的结果图,发现软阈值去噪后的图像比硬阈值去噪后的图像效果好,我们设计的折中阈值去噪后的结果图达到了最好的清晰度。
4.2 去噪系数

由上表可以看出,经过小波阈值去噪后,PSNR有了明显的提高,这表明我们设计的小波阈值去噪方法对具有高斯白噪声的图像去噪具有较好的效果。同时,我们比较表中硬阈值、软阈值、随机折中阈值和最佳阈值可以得出以下结论:软阈值相对于硬阈值具有更好的图像去噪效果;我们设计的优化阈值取得了最好的效果,这表明我们的优化阈值融合了硬阈值和软阈值的优点,表现出更好的图像去噪能力。
4.3 折中系数曲线图
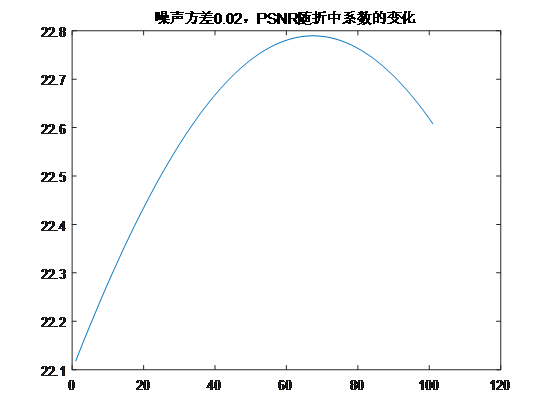
我们选取了均值为0,方差0.02的高斯噪声作为输入来得到PSNR随折中系数变化的曲线图。由图中可以看出,PSNR随折中系数呈凸函数形状,折中系数为0时是硬阈值,折中系数为100时是软阈值,大约在折中系数为70的时候,PSNR达到了最大值。
总结
本文提出了一种小波去噪的方法,选择一幅图像加入不同程度的高斯噪声,对带噪图片进行小波分解,利用改进的阈值对小波系数进行阈值处理,利用处理后的图像重构原始图像,并通过计算峰值信噪比(PSNR)判断去噪效果。结果表明,所提出的方法对于受高斯白噪声污染的图像具有较好的恢复能力,改进的阈值相比软阈值和硬阈值具有更好的图像去噪性能。
本次课程设计没有将基于小波变换的阈值去噪方法和其他方法进行比较,无法体现小波变换的优势。同时,我们的设计性能仍有待提高,需要不断的改进。
在未来的研究中,可以将不同的图像去噪方法进行比较,也可以加入滤波器进行更复杂的图像去噪设计。