mh采样算法推导_采样算法简述

1 阅读之前

在阅读本文之前请先明确什么是样本。
前置：假设一个样本取自分布p(x)，那么我们通常将其记录为
，但本文使用的小写字母加下标的方式表示样本
。
前置：单个样本是无法研究分布的，只有样本数量足够时才能研究性质。

2 均匀分布随机数的产生

在获取均匀分布的随机数后可以通过后续的算法来获取其他分部的随机数。最简单的方式是对坐标进行变换。假设

是原始空间中的坐标，而

是变换空间后的坐标。定义函数

和坐标变换：

此时假设函数

为概率密度函数，而到目前为止仅能获取均匀分布的随机数，因此概率密度函数定义为

定义变换：

概率密度函数有积分意义：

变换域面积与原空间面积关系为：

其中

为雅克比，因此函数可以转换为：

所以均匀分布的样本可以产生标准正态分布的样本。
对于坐标变换而言，还有更加通用的方式。假设

是(0-1)区间均匀分布的样本。而我们想获取的分布为

。记录：

定义坐标变换

变量

的累计分布函数为：

所以如果

的话就是所需分布样本。对于难以计算的情况，我们可以使用近似的方式来计算概率：

import numpy as np 
def p(x):
    """
    所需概率密度函数
    """
 return np.exp(-x**2/2)/np.pi/2
def sampler():
    """
    生成一个随机样本
    """
    # 产生多个样本
    xs = np.random.random([20]) * 10 - 5
    # 计算概率
    ps = p(xs)
    # 计算累计概率
    t = np.cumsum(ps)/np.sum(ps)
    # 产生均匀分布随机数
    u = np.random.random()
    # 根据概率选择样本
    sample_id = int(np.searchsorted(t, np.random.random()))
    return xs[sample_id]
# 给定初始值
x_samples = [] 
n_samples = 5000

for itr in range(n_samples):
    x_samples.append(sampler()) 
x_samples = np.array(x_samples)
import matplotlib.pyplot as plt 
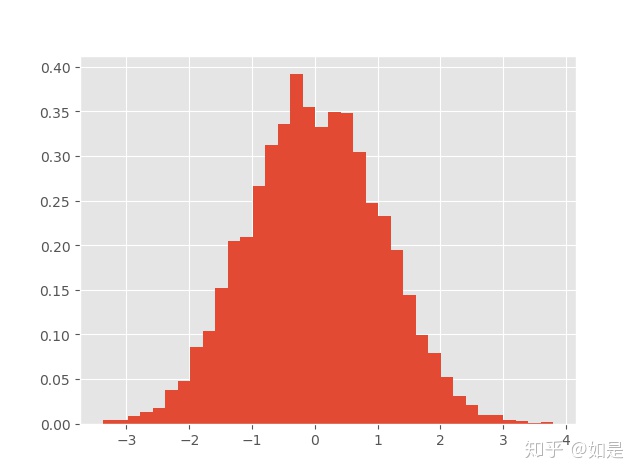
plt.hist(x_samples)
plt.show()

所得结果

3 通过拒绝部分样本获取所需分布

3.1 拒绝接受采样

均匀分布样本与其他分布样本区别就在于一些低概率样本出现过多，因此可以使用拒绝部分样本的方式对样本进行采样。假设需要的分布为

。其他分部样本为

。二者之间关系为

为使得

在之前乘以一个乘子。那么采样过程为：

从分布q中产生样本
根据接受率
接受样本

产生均匀分布随机数
，如果
则接受样本。

根据这个方法举个例子，产生二维正态分布的随机数。

"""
用于演示拒绝接受采样算法
"""
import numpy as np 
def p(x):
    """
    所需概率密度函数
    """
    return np.exp(-np.sum(x**2)/2)/np.pi/2
def q(x):
    """
    原始样本的概率密度函数
    """
    return 1/100
# 产生均匀分布的样本
x = np.random.random([10000, 2]) * 10 - 5
# 选择后样本
x_accept = []
x_reject = []
c = 100/np.pi/2
for itr in x:
    alpha = p(itr) / q(itr) / c
    # 产生阈值
    s = np.random.random() 
    if s < alpha:
        x_accept.append(itr)
    else:
        x_reject.append(itr)

x_accept = np.array(x_accept)
x_reject = np.array(x_reject)

# 绘图
import matplotlib.pyplot as plt 
plt.subplot(121)
x_norm = np.random.normal(0, 1, [1000, 2])
plt.scatter(x_norm[:, 0], x_norm[:, 1])
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.subplot(122)
plt.scatter(x_accept[:, 0], x_accept[:, 1], marker='o', color="#000099", alpha=1.0)
plt.scatter(x_reject[:, 0], x_reject[:, 1], marker='+', color="#990000", alpha=0.5)
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.show()

结果

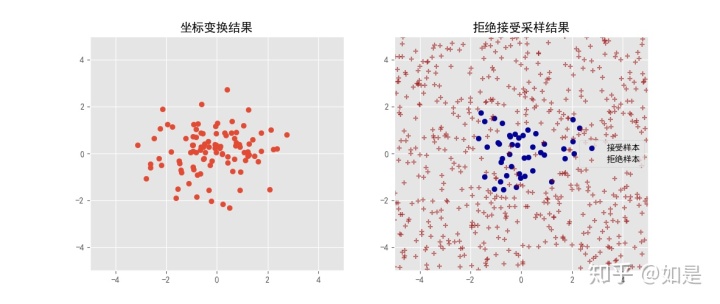
3.2 Metropolis-Hastings采样

通过运行上述程序可以看到，通过拒绝接受样本在计算过程中有大量计算是无用的。因此选取合适的分布

是十分必要的。但这通常都很难获得。由此产生出了新的Metropolis-Hastings（MH）算法。下面对算法进行详细描述。

在拒绝接受采样的过程中发现，每个样本产生的过程是完全独立的。这符合随机数产生的逻辑。但如果将采样看作一个过程，那么随机数产生的过程并非完全独立的.。依然以上面的例子来说，我们产生了一个均匀分布的随机数。而我们所期望的分布是标准的二维正态分布。这需要我们拒绝部分样本。到此为止与拒绝接受采样都没有什么不同。但是假设我们已经产生了一个概率非常小的样本x，那么之后的样本应当比x大一些才能平衡采到x所带来的影响。由此可以将采样看作一个过程：

作为采样过程，我们希望在采样过程中概率不变，也就是一个平稳的过程：

这里定义一个转移矩阵

：

当

时，上式变为：

等式恒成立，因此条件也称为细致平稳条件。满足细致平稳条件的样本，概率是分布是平稳的。这个过程并不是完整的证明。通常转移概率

是非常难以获得的。因此我们会构造一个符合细致平稳条件的

，比如

定义

因此Metropolis-Hastings算法为

从条件概率
中产生新样本

产生均匀分布

如果
则接受采样

使用上述算法，产生二维正态分布的随机数。原始样本产生过程中我们依然使用均匀分布样本。这些样本每个采到的几率均是相同的，因此转移矩阵

此时


"""
用于演示Metropolis-Hastings算法
"""
import numpy as np 
def p(x):
    """
    所需概率密度函数
    """
    return np.exp(-np.sum(x**2)/2)/np.pi/2
def cal_alpha(x1, x2):
    return np.min([p(x2)/p(x1), 1])

# 产生均匀分布的样本
x = np.random.random([1000, 2]) * 10 - 5
# 选择后样本
x_accept = []
x_reject = []
c = 100/np.pi/2
x_accept.append(x[0])
for itr in range(len(x)-1):
    alpha = cal_alpha(x_accept[-1], x[itr+1])
    s = np.random.random() 
    if s < alpha:
        x_accept.append(x[itr+1])
    else:
        x_accept.append(x_accept[-1])
        x_reject.append(x[itr+1])

x_accept = np.array(x_accept)
x_reject = np.array(x_reject)

# 绘图
import matplotlib.pyplot as plt 
plt.subplot(121)
x_norm = np.random.normal(0, 1, [1000, 2])
plt.scatter(x_norm[:, 0], x_norm[:, 1])
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.subplot(122)
plt.scatter(x_accept[:, 0], x_accept[:, 1], marker='o', color="#000099", alpha=1.0)
plt.scatter(x_reject[:, 0], x_reject[:, 1], marker='+', color="#990000", alpha=0.5)
plt.plot(x_accept[:, 0], x_accept[:, 1], color="#000099", alpha=0.3)
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.show()

计算结果

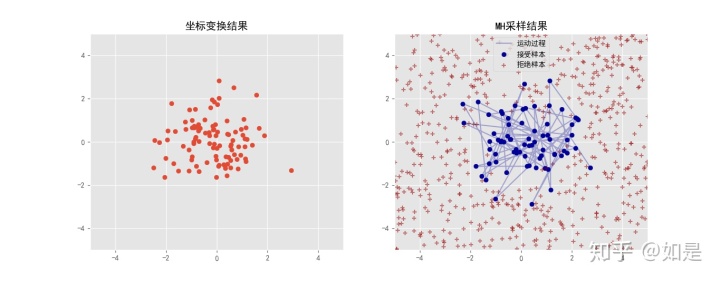
3.3 吉布斯采样
上面的采样过程与状态转移的方式以及转移矩阵的选择上实际上并无太大关系。可以发现MH算法的的基本过程就是选择一个样本

并计算其概率

，如果新生成一个样本

其概率

，如果新的样本j的概率大于i的概率那么我们就接受它，因为比它概率小的样本都接受了。如果j的概率小于i的概率，那么我们就按照二者概率之差来随机决定是否接受此样本。这个过程依然会拒绝样本，在高维时则更加难以采样。

现在我们假设采样过程中先后生成了两个样本

，二者仅在坐标i上是不同的。此时二者概率为

其中

代表x中不含i的元素，由于只有i不同，所以

。上式是我们对联合概率进行的分解。由于

，所以

这是符合细致平稳条件的。

"""
用于演示吉布斯采样算法
"""
import numpy as np 
def p(x):
    """
    所需概率密度函数
    """
    return np.exp(-np.sum(x**2, axis=1)/2)/np.pi/2
def dim_sampler(x, dim):
    """
    从某个维度采样
    直接计算多个样本的概率，根据概率选择合适的样本。
    由于仅是一维分布，我们也可以用其他方式进行采样。
    """
    # 产生多个样本
    sp = np.random.random([20]) * 10 - 5
    xs = np.ones([20, len(x)])*np.array(x)
    xs[:, dim] = sp
    # 计算概率
    ps = p(xs)
    # 根据概率选择样本
    t = np.cumsum(ps)/np.sum(ps)
    s = np.random.random()
    sample_id = np.searchsorted(t, s)
    return list(xs[sample_id])
# 给定初始值
x_samples = [[0, 0]]
n_samples = 600
state = x_samples[-1]
for itr in range(n_samples):
    for dim in range(len(state)):
        state = dim_sampler(state, dim)
        x_samples.append(state)
x_samples = np.array(x_samples)
import matplotlib.pyplot as plt 
plt.subplot(121)
x_norm = np.random.normal(0, 1, [1000, 2])
plt.scatter(x_norm[:, 0], x_norm[:, 1])
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.subplot(122)
plt.scatter(x_samples[:, 0], x_samples[:, 1], marker='o', color="#000099", alpha=1.0)
plt.plot(x_samples[:, 0], x_samples[:, 1], color="#000099", alpha=0.3)
plt.xlim([-5, 5])
plt.ylim([-5, 5])
plt.show()

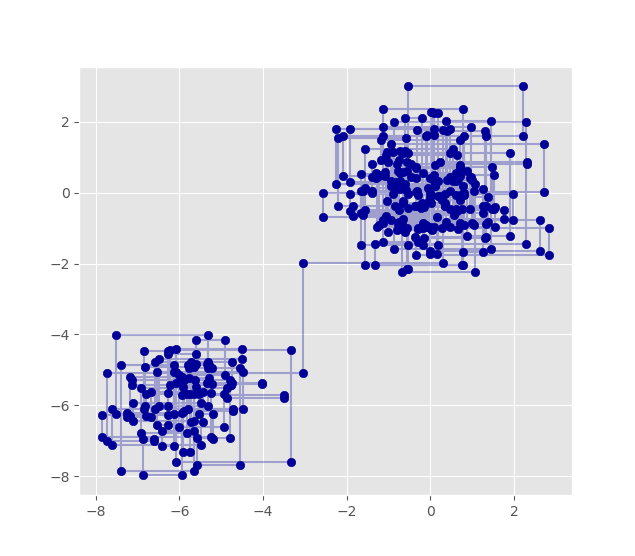
所得结果

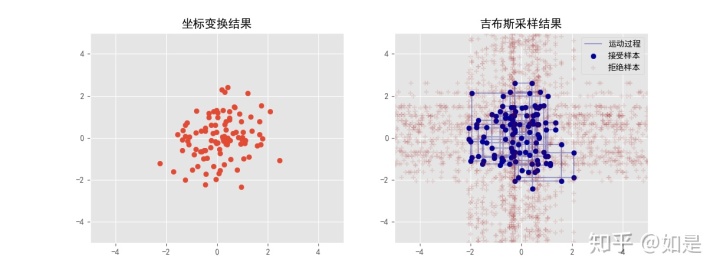
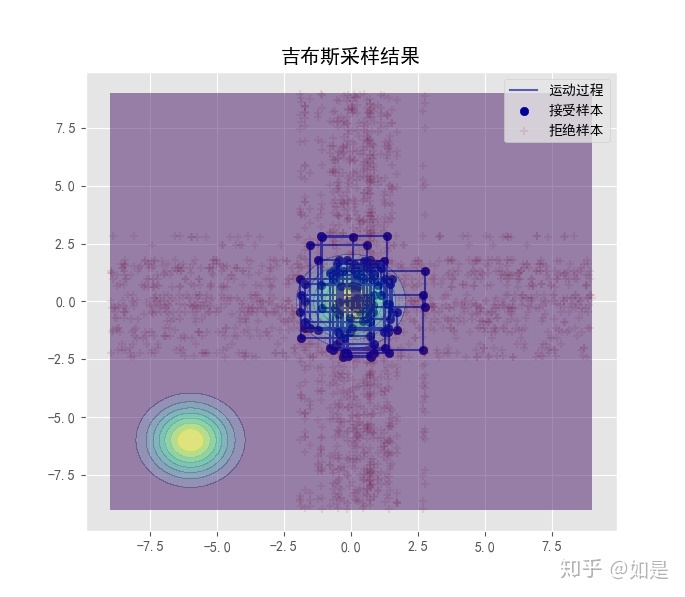
对于吉布斯采样来说，如果有多个峰，那么采样过程中可能出现转移概率过低，无法采集到的问题：

原文链接：https://blog.csdn.net/weixin_34546240/article/details/112460370