背景

大一做项目，使用过huff模型与gwr模型（地理加权回归）的线性化。在处理数据过程中也遇到了平滑数据处理的问题。这里做一个总结记录。

非线性模型转换为线性模型

背景

模型可以分为线性模型和非线性模型，有时候为了处理需要将线性模型转换为非线性模型，如地理加权回归模型只能适用于线性数据，而huff模型是非线性模型，两种模型结合的一个方法就是将huff模型线性化，再利用地理加权回归进行线性回归分析。

非线性关系线性化的几种情况

一般我们可以直接对模型两侧取对数，转换为线性模型，例如：
对于指数曲线 $y=d{e}^{bx}$ ，令 $y^{{}^{\prime }}=l{n}^y$,可以将其转化为直线形式： $y^{{}^{\prime }}=a+b{x}^{{}^{\prime }}$，其中$a=l{n}^d$；

对于幂函数曲线$y=d{x}^b$，令$y^{{}^{\prime }}=l{n}^y$，$x^{{}^{\prime }}=l{n}^x$，可以将其转
化为直线形式：$y^{{}^{\prime }}=a+b{x}^{{}^{\prime }}$其中，$a=l{n}^d$；

其他的情况可以将非线性的x、y整体视为未知数进行替换。如把
$x^{{}^{\prime }}视为n^x$：

对于对数曲线$y=a+bl{n}^x$，令$y^{{}^{\prime }}=y$，$x^{{}^{\prime }}=l{n}^x$，可以将其转化为直线形式：$y^{{}^{\prime }}=a+b{x}^{{}^{\prime }}$；

对于双曲线$\frac{1}{y}=a+\frac{1}{x}$，令$y^{{}^{\prime }}=\frac{1}{y}$，$x^{{}^{\prime }}=\frac{1}{x}$，转化为直线形式：$y^{{}^{\prime }}=a+b{x}^{{}^{\prime }}$；

应用

对原始竞争选址模型进行线性变换是应用地理加权回归模型的前提。这是因为地理加权回归模型只能适用于线性模型，对于非线性模型则需要对其进行线性变换。本文应用 NC 变换（Nakanishi and Cooper’s transformation）对模型进行处理，使其无损变换为线性模型。本文以 Huff 模型敏感参数的评估精度来度量选址的竞争。Huff 模型作为竞争选址的主要方法，是一种非线性模型。为了探索Huff 模型敏感参数的空间异质性，需要对其进行线性变换。Huff 模型变换以后，如下式所示：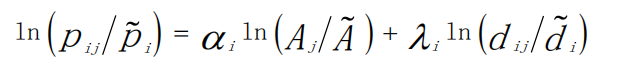
通过gwr回归后的结果具有了空间异质性。能够反映不同空间商圈的吸引力。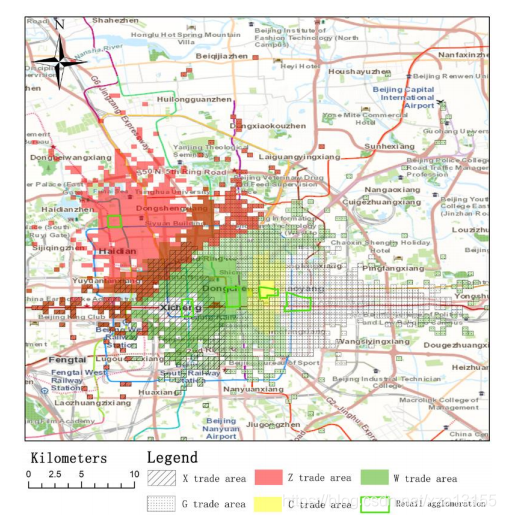

平滑数据处理

在数据处理中，经常要计算数据出现的概率估计。但是，算法训练的时候，可能会出现值为零的数据，人们发明了不少可以改善新数据出现的概率算法，即数据的平滑。最常见的数据平滑思路包括如下几种：
1，对0值直接+1
2，加k，k可以是一个很小的值。
如：$B_i=[\frac{a}{N}\ast I+(1-a)A]B_{i-1}$；a为一个很小的值。

参考文献

[1]Jiang, W.; Wang, Y.; Dou, M.; Liu, S.; Shao, S.; Liu, H. Solving Competitive Location Problems with Social Media Data Based on Customers’ Local Sensitivities. ISPRS Int. J. Geo-Inf. 2019, 8, 202. https://doi.org/10.3390/ijgi8050202
[2] 吴军， 数学之美
[3] https://blog.csdn.net/fuermolei/article/details/81353746

新开通了本人的公众号，欢迎关注：燕南路GISer ，专注GIS干货分享，不定期更新。
主要兴趣：GIS、时空数据挖掘、python、机器学习深度学习
CSDN的部分内容会重写再搬迁到公众号，欢迎关注！