本篇来看一个具体的能量方程,以 twoPhaseEulerFoam 的 EEqn.H 为例。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | {
volScalarField& he1 = thermo1.he();
volScalarField& he2 = thermo2.he();
volScalarField Cpv1("Cpv1", thermo1.Cpv());
volScalarField Cpv2("Cpv2", thermo2.Cpv());
volScalarField heatTransferCoeff(fluid.heatTransferCoeff());
fvScalarMatrix he1Eqn
(
fvm::ddt(alpha1, rho1, he1) + fvm::div(alphaRhoPhi1, he1)
- fvm::Sp(contErr1, he1)
+ fvc::ddt(alpha1, rho1, K1) + fvc::div(alphaRhoPhi1, K1)
- contErr1*K1
+ (
he1.name() == thermo1.phasePropertyName("e")
? fvc::ddt(alpha1)*p + fvc::div(alphaPhi1, p)
: -alpha1*dpdt
)
- fvm::laplacian
(
fvc::interpolate(alpha1)
*fvc::interpolate(thermo1.alphaEff(phase1.turbulence().mut())),
he1
)
);
he1Eqn.relax();
he1Eqn -=
(
heatTransferCoeff*(thermo2.T() - thermo1.T())
+ heatTransferCoeff*he1/Cpv1
- fvm::Sp(heatTransferCoeff/Cpv1, he1)
+ fvOptions(alpha1, rho1, he1)
);
|
对应的能量方程为(忽略fvOptions)

代码里剩下的两项,
1 2 | + heatTransferCoeff*he1/Cpv1 - fvm::Sp(heatTransferCoeff/Cpv1, he1) |
含义暂不明。这两项,其实是同一个公式,只是前者是显示处理,后者用了隐式源项,估计是为了数值稳定性的目的而构建的。
前面提过,对于如下设置,
1 2 3 4 5 6 7 8 9 10 | thermoType
{
type heRhoThermo;
mixture pureMixture;
transport const;
thermo hConst;
equationOfState perfectGas;
specie specie;
energy sensibleInternalEnergy;
}
|
最终,thermo 指针指向的是 heRhoThermo 类的对象,所以,从 heRhoThermo 类的构造函数看起:
1 2 3 4 5 6 7 8 9 10 11 | template<class BasicPsiThermo, class MixtureType>
Foam::heRhoThermo<BasicPsiThermo, MixtureType>::heRhoThermo
(
const fvMesh& mesh,
const word& phaseName
)
:
heThermo<BasicPsiThermo, MixtureType>(mesh, phaseName)
{
calculate(); // 构造函数调用 calculate 函数来初始化所有的热物理相关量
}
|
calculate()函数
可见,构造函数里调用了 calculate 函数,前面提过,这个函数的作用是更新各个热物理相关量。
接下来一个一个来看里面涉及到的函数。
he
he 其实是 “h or e”,具体是焓,还是内能,取决于 energy 这一项的设置。 he 函数在 heThermo 类中定义,返回的是数据成员 he_,所以这里需要看一下数据成员 he_ 的初始化:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 | template<class BasicThermo, class MixtureType>
Foam::heThermo<BasicThermo, MixtureType>::heThermo
(
const fvMesh& mesh,
const dictionary& dict,
const word& phaseName
)
:
BasicThermo(mesh, dict, phaseName),
MixtureType(*this, mesh),
he_
(
IOobject
(
BasicThermo::phasePropertyName
(
MixtureType::thermoType::heName()
),
mesh.time().timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh,
dimEnergy/dimMass,
this->heBoundaryTypes(),
this->heBoundaryBaseTypes()
)
{
init();
}
|
这里调用的 init 函数的内容为
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | template<class BasicThermo, class MixtureType>
void Foam::heThermo<BasicThermo, MixtureType>::init()
{
scalarField& heCells = he_.internalField();
const scalarField& pCells = this->p_.internalField();
const scalarField& TCells = this->T_.internalField();
forAll(heCells, celli)
{
heCells[celli] =
this->cellMixture(celli).HE(pCells[celli], TCells[celli]);
}
forAll(he_.boundaryField(), patchi)
{
he_.boundaryField()[patchi] == he
(
this->p_.boundaryField()[patchi],
this->T_.boundaryField()[patchi],
patchi
);
}
this->heBoundaryCorrection(he_);
}
|
这里调用了 HE 函数来初始化 he_ 的内部场,并对调用另一个三个数的 he 函数其边界条件进行了修正:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 | template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::scalarField> Foam::heThermo<BasicThermo, MixtureType>::he
(
const scalarField& p,
const scalarField& T,
const label patchi
) const
{
tmp<scalarField> the(new scalarField(T.size()));
scalarField& he = the();
forAll(T, facei)
{
he[facei] =
this->patchFaceMixture(patchi, facei).HE(p[facei], T[facei]);
// 本质上还是调用了 HE 函数
}
return the;
}
|
再来看 HE 函数,这个函数看名字和参数,应该是根据压力和温度来计算能量的,其定义在 species::thermo 类:
1 2 3 4 5 6 | template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::HE(const scalar p, const scalar T) const
{
return Type<thermo<Thermo, Type> >::HE(*this, p, T);
}
|
这里,由于能量最终是什么形式,取决于 energy 关键字对应的类,所以,这里也是调用了定义在前面提到的 energy variable 类中的 HE 函数,以 sensibleInternalEnergy 为例:
1 2 3 4 5 6 7 8 9 | scalar HE
(
const Thermo& thermo,
const scalar p,
const scalar T
) const
{
return thermo.Es(p, T);
}
|
可见,其返回的是 species::thermo 类的 Es 函数,
1 2 3 4 5 6 7 8 9 10 11 12 13 | template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Es(const scalar p, const scalar T) const
{
return this->es(p, T)/this->W();
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::es(const scalar p, const scalar T) const
{
return this->hs(p, T) - p*this->W()/this->rho(p, T);
}
|
hs 函数定义在 thermo 类型的类中,以 hConstThermo 类为例:
1 2 3 4 5 6 7 8 | template<class equationOfState>
inline Foam::scalar Foam::hConstThermo<equationOfState>::hs
(
const scalar p, const scalar T
) const
{
return Cp_*T;
}
|
hs 表示的是显焓,等于 Cp_*T 。 es 是内能,根据焓的定义,H=U+pVH=U+pV。代码中的 hs 和 es 都是 J/kMol 的量纲,所以,es=hs−pV/nes=hs−pV/n 。以理想气体状态方程为例,pV=nRTpV=nRT,或者写成 pM=ρRTpM=ρRT,得 pV/n=RT=pM/ρpV/n=RT=pM/ρ 。
注意,这里的 Cp_,在字典文件里给的是 J/(kg.K) 量纲的,但是在构造函数中,将其转成了 J/(kmol.K) 的量纲:
1 2 3 4 5 6 7 8 9 10 | template<class equationOfState>
Foam::hConstThermo<equationOfState>::hConstThermo(const dictionary& dict)
:
equationOfState(dict),
Cp_(readScalar(dict.subDict("thermodynamics").lookup("Cp"))),
Hf_(readScalar(dict.subDict("thermodynamics").lookup("Hf")))
{
Cp_ *= this->W();
Hf_ *= this->W();
}
|
所以,hs, es 是 J/kmol ; Es, HE 是 J/kg。
Cpv
这个函数定义在 heThermo 类中。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::Cpv() const
{
const fvMesh& mesh = this->T_.mesh();
tmp<volScalarField> tCpv
(
new volScalarField
(
IOobject
(
"Cpv",
mesh.time().timeName(),
mesh,
IOobject::NO_READ,
IOobject::NO_WRITE
),
mesh,
dimEnergy/dimMass/dimTemperature
)
);
volScalarField& cpv = tCpv();
forAll(this->T_, celli)
{
cpv[celli] =
this->cellMixture(celli).Cpv(this->p_[celli], this->T_[celli]);
}
forAll(this->T_.boundaryField(), patchi)
{
const fvPatchScalarField& pp = this->p_.boundaryField()[patchi];
const fvPatchScalarField& pT = this->T_.boundaryField()[patchi];
fvPatchScalarField& pCpv = cpv.boundaryField()[patchi];
forAll(pT, facei)
{
pCpv[facei] =
this->patchFaceMixture(patchi, facei).Cpv(pp[facei], pT[facei]);
}
}
return tCpv;
}
|
这个函数,创建了一个 tmp<volScalarField>,然后调用定义在 species::thermo 类中的两参数 Cpv 函数来对场量进行初始化,这个函数的形式如下
1 2 3 4 5 6 7 8 9 10 11 12 13 | template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::Cpv(const scalar p, const scalar T) const
{
return this->cpv(p, T)/this->W();
}
template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::cpv(const scalar p, const scalar T) const
{
return Type<thermo<Thermo, Type> >::cpv(*this, p, T);
}
|
cpv 函数返回的是定义在 energy variable 类中的三参数 cpv 函数,对于 sensibleInternalEnergy,
1 2 3 4 5 6 7 8 9 | scalar cpv
(
const Thermo& thermo,
const scalar p,
const scalar T
) const
{
return thermo.cv(p, T);
}
|
这里返回的是 species::thermo 类的 cv 函数,
1 2 3 4 5 6 | template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::cv(const scalar p, const scalar T) const
{
return this->cp(p, T) - this->cpMcv(p, T);
}
|
这里的 cp 函数定义在 thermo 类型的类中,以 hConst 为例
1 2 3 4 5 6 7 8 9 | template<class equationOfState>
inline Foam::scalar Foam::hConstThermo<equationOfState>::cp
(
const scalar p,
const scalar T
) const
{
return Cp_; // 量纲是 J/(kmol.K)
}
|
cpMcv 的定义在状态方程类中,以 perfectGas 为例
1 2 3 4 5 | template<class Specie>
inline Foam::scalar Foam::perfectGas<Specie>::cpMcv(scalar, scalar) const
{
return this->RR; // 量纲是 J/(kmol.K),所以值应该是 8314
}
|
alphaEff
这个函数需要一个参数,其定义在 heThermo 类中
1 2 3 4 5 6 7 8 9 10 11 | template<class BasicThermo, class MixtureType>
Foam::tmp<Foam::volScalarField>
Foam::heThermo<BasicThermo, MixtureType>::alphaEff
(
const volScalarField& alphat
) const
{
tmp<Foam::volScalarField> alphaEff(this->CpByCpv()*(this->alpha_ + alphat));
alphaEff().rename("alphaEff");
return alphaEff;
}
|
这里, 无参数的 CpByCpv 函数定义在 species::thermo 类中,最终调用的是 energy varialble 类中的 CpByCpv 函数,如果是内能形式的,则返回 thermo.gamma(p, T) ,焓形式则返回 1。 gamma 的定义在 species::thermo
1 2 3 4 5 6 7 | template<class Thermo, template<class> class Type>
inline Foam::scalar
Foam::species::thermo<Thermo, Type>::gamma(const scalar p, const scalar T) const
{
scalar cp = this->cp(p, T);
return cp/(cp - this->cpMcv(p, T));
}
|
alpha_ 是层流能量扩散系数,定义在 basicThermo 类,并在该类的构造函数中初始化为零。在 heRhoThermo 类的 calculate 函数中,对其进行了更新
1 2 3 4 5 | scalarField& alphaCells = this->alpha_.internalField(); alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]); fvPatchScalarField& palpha = this->alpha_.boundaryField()[patchi]; palpha[facei] = mixture_.alphah(pp[facei], pT[facei]); |
可见, alpha_ 的值是通过 alphah 函数来计算更新的,这个函数的定义在 trasnport 模型里,以 constTransport 为例
1 2 3 4 5 6 7 8 9 | template<class Thermo>
inline Foam::scalar Foam::constTransport<Thermo>::alphah
(
const scalar p,
const scalar T
) const
{
return mu(p, T)*rPr_;
}
|
返回粘度与普朗特数的比值。
至于 alphat ,则是函数 alphaEff 的参数,根据开头的代码可知, alphat 其实是 mut 。
只是,暂时不知道为什么有效热扩散系数 alphaEff = CpByCpv * (alpha + alphat)。
构建起能量方程后,就该对其进行求解了。
1 2 3 4 5 6 7 8 9 10 11 12 13 | fvOptions.constrain(he1Eqn);
he1Eqn.solve();
fvOptions.constrain(he2Eqn);
he2Eqn.solve();
thermo1.correct();
Info<< "min " << thermo1.T().name()
<< " " << min(thermo1.T()).value() << endl;
thermo2.correct();
Info<< "min " << thermo2.T().name()
<< " " << min(thermo2.T()).value() << endl; |
correct()函数
这里, solve 函数值得细说,重点是看 correct() 函数,以及 T() 函数。
corretc() 函数指的是定义在 heRhoThermo 类中的 correct() 函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | template<class BasicPsiThermo, class MixtureType>
void Foam::heRhoThermo<BasicPsiThermo, MixtureType>::correct()
{
if (debug)
{
Info<< "entering heRhoThermo<MixtureType>::correct()" << endl;
}
calculate();
if (debug)
{
Info<< "exiting heRhoThermo<MixtureType>::correct()" << endl;
}
}
|
可见, correct() 函数,其实就是对 calculate 函数进行了一次调用而已。
看来最核心最关键的就在 calculate 函数中了。在仔细看这个函数之前,先把 T() 的定义看完。 T() 定义在 basicThermo 类中,其作用仅是返回同样定义在 basicThermo 类中定义的数据成员 T_ 而已。
下面深入分析一下 heRhoThermo 类中的 calculate 函数,这里再将它列出来一次:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 | template<class BasicPsiThermo, class MixtureType>
void Foam::heRhoThermo<BasicPsiThermo, MixtureType>::calculate()
{
const scalarField& hCells = this->he().internalField();
const scalarField& pCells = this->p_.internalField();
scalarField& TCells = this->T_.internalField();
scalarField& psiCells = this->psi_.internalField();
scalarField& rhoCells = this->rho_.internalField();
scalarField& muCells = this->mu_.internalField();
scalarField& alphaCells = this->alpha_.internalField();
forAll(TCells, celli)
{
const typename MixtureType::thermoType& mixture_ =
this->cellMixture(celli);
TCells[celli] = mixture_.THE
(
hCells[celli],
pCells[celli],
TCells[celli]
);
psiCells[celli] = mixture_.psi(pCells[celli], TCells[celli]);
rhoCells[celli] = mixture_.rho(pCells[celli], TCells[celli]);
muCells[celli] = mixture_.mu(pCells[celli], TCells[celli]);
alphaCells[celli] = mixture_.alphah(pCells[celli], TCells[celli]);
}
forAll(this->T_.boundaryField(), patchi)
{
fvPatchScalarField& pp = this->p_.boundaryField()[patchi];
fvPatchScalarField& pT = this->T_.boundaryField()[patchi];
fvPatchScalarField& ppsi = this->psi_.boundaryField()[patchi];
fvPatchScalarField& prho = this->rho_.boundaryField()[patchi];
fvPatchScalarField& ph = this->he().boundaryField()[patchi];
fvPatchScalarField& pmu = this->mu_.boundaryField()[patchi];
fvPatchScalarField& palpha = this->alpha_.boundaryField()[patchi];
if (pT.fixesValue())
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
ph[facei] = mixture_.HE(pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
prho[facei] = mixture_.rho(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
else
{
forAll(pT, facei)
{
const typename MixtureType::thermoType& mixture_ =
this->patchFaceMixture(patchi, facei);
pT[facei] = mixture_.THE(ph[facei], pp[facei], pT[facei]);
ppsi[facei] = mixture_.psi(pp[facei], pT[facei]);
prho[facei] = mixture_.rho(pp[facei], pT[facei]);
pmu[facei] = mixture_.mu(pp[facei], pT[facei]);
palpha[facei] = mixture_.alphah(pp[facei], pT[facei]);
}
}
}
}
|
这个函数是在对几个热物理相关的量来进行更新,先更新内部场,再更新边界值。一个一个来看:
he
he 前面讲了,这里需要注意的是其边界值的更新。由于
he没有IO,其内部场量通过求解能量方程来更新,边界则需要根据情况特殊处理。两种情况,一种是设定了边界的温度值(pT.fixesValue()),这时需要更新边界上的he值:ph[facei] = mixture_.HE(pp[facei], pT[facei]);否则,则边界上的he不需要特殊地更新。psi
这个直接调用两参数的
psi函数来更新,这个函数的定义在状态方程里,以perfaceGas为例,1 2 3 4 5
template<class Specie> inline Foam::scalar Foam::perfectGas<Specie>::psi(scalar, scalar T) const { return 1.0/(this->R()*T); }
psi 是压缩因子,返回 1RT1RT。
rho
- 这个调用的是两参数的
rho函数,定义在状态方程类中,用于密度的更新,同样以perfaceGas为例,1 2 3 4 5
template<class Specie> inline Foam::scalar Foam::perfectGas<Specie>::rho(scalar p, scalar T) const { return p/(this->R()*T); }
返回 pRTpRT。
mu
- 这个调用的是两参数的
mu函数,其定义在 transport 类中,以constTransport为例,这个返回的是场量的层流粘度1 2 3 4 5 6 7 8 9
template<class Thermo> inline Foam::scalar Foam::constTransport<Thermo>::mu ( const scalar p, const scalar T ) const { return mu_; // 常量 }
alphah 上面说过了,不再重复。
最后,最复杂的就是温度的更新了
T
- 温度的更新,调用的是三参数的
THE函数,这个函数定义在species::thermo类中,1 2 3 4 5 6 7 8 9 10
template<class Thermo, template<class> class Type> inline Foam::scalar Foam::species::thermo<Thermo, Type>::THE ( const scalar he, const scalar p, const scalar T0 ) const { return Type<thermo<Thermo, Type> >::THE(*this, he, p, T0); }
这里,调用的是 energy variable 类的 THE 函数,以 sensibleInternalEnergy 为例,
1 2 3 4 5 6 7 8 9 10 | scalar THE
(
const Thermo& thermo,
const scalar e,
const scalar p,
const scalar T0
) const
{
return thermo.TEs(e, p, T0);
}
|
可见,对于 sensibleInternalEnergy , THE 函数实际上返回的是 species::thermo 类的 TEs 函数。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 | template<class Thermo, template<class> class Type>
inline Foam::scalar Foam::species::thermo<Thermo, Type>::TEs
(
const scalar es,
const scalar p,
const scalar T0
) const
{
return T
(
es,
p,
T0,
&thermo<Thermo, Type>::Es,
&thermo<Thermo, Type>::Cv,
&thermo<Thermo, Type>::limit
);
}
|
这里,终于来到了这个六参数的 T 函数:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 | // 声明
inline scalar T
(
scalar f,
scalar p,
scalar T0,
scalar (thermo::*F)(const scalar, const scalar) const,
scalar (thermo::*dFdT)(const scalar, const scalar) const,
scalar (thermo::*limit)(const scalar) const
) const;
//实现
template<class Thermo, template<class> class Type>
inline Foam::scalar Foam::species::thermo<Thermo, Type>::T
(
scalar f,
scalar p,
scalar T0,
scalar (thermo<Thermo, Type>::*F)(const scalar, const scalar) const,
scalar (thermo<Thermo, Type>::*dFdT)(const scalar, const scalar)
const,
scalar (thermo<Thermo, Type>::*limit)(const scalar) const
) const
{
scalar Test = T0;
scalar Tnew = T0;
scalar Ttol = T0*tol_;
int iter = 0;
do
{
Test = Tnew;
Tnew =
(this->*limit)
(Test - ((this->*F)(p, Test) - f)/(this->*dFdT)(p, Test));
if (iter++ > maxIter_)
{
FatalErrorIn
(
"thermo<Thermo, Type>::T(scalar f, scalar T0, "
"scalar (thermo<Thermo, Type>::*F)"
"(const scalar) const, "
"scalar (thermo<Thermo, Type>::*dFdT)"
"(const scalar) const, "
"scalar (thermo<Thermo, Type>::*limit)"
"(const scalar) const"
") const"
) << "Maximum number of iterations exceeded"
<< abort(FatalError);
}
} while (mag(Tnew - Test) > Ttol);
return Tnew;
}
|
这个函数,前三个参数是普通的 scalar 类型变量,后三个参数,是函数指针,并且都指向当前类 species::thermo 的成员函数。以 TEs 为例,后三个参数分别代入的是 Es , Cv 以及 limit 三个函数。 Es 和 Cv 前面都看过了, limit 定义在 thermo 类中,以 hConst 为例,
1 2 3 4 5 6 7 8 | template<class EquationOfState>
inline Foam::scalar Foam::hConstThermo<EquationOfState>::limit
(
const scalar T
) const
{
return T;
}
|
直接返回温度 T 。事实上,除了 janaf 模型,其他的都是返回 T 。 janaf 模型中, 如果温度没有超出 [Tlow,Thigh],则会出来警告信息,并且,若 T < Tlow 则返回 Tlow,而 T > Thigh 时,则返回 Thigh。
下面仔细来分析六参数 T 函数的核心部分。经过摸索,发现这个其实是一个牛顿迭代的过程,目的是根据 Es 函数,从内能 es 来计算温度 T,即求解 Es(p,T)−Es=0Es(p,T)−Es=0 。令 F(T)=Es(p,T)−EsF(T)=Es(p,T)−Es,则牛顿迭代法的递推公式为

对于 sensibleInternalEnergy ,
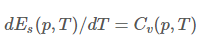
所以最终得到递推公式为
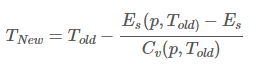
这里设置了最大迭代次数为 100,超过将报那个涉及到能量的模拟中最容易见到的崩溃信息:”Maximum number of iterations exceeded” 。
当能量变量是焓时,则 EsEs 要换成 HsHs, CvCv 要换成 CpCp 。
至此便分析完了一个具体的能量方程实例。