A. Candies
题意:给一个n,让求一个x,使得 x+2x+4x+⋯+2k−1x = n
思路:转换一下等式就是 x = n / (1+2+4+…+2k−1),题目要求x是整数。那也就是说,n是整除于那一大坨的。并且题目保证有解。那么就暴力枚举k就好了嘛,找到一个使得n整除于他们的和的就行了。
AC代码:
#include <bits/stdc++.h>
#define int long long
#define mk make_pair
using namespace std;
const int N = 3e5+11;
const int mod = 1e9+7;
int t,n,m,k;
int a[N];
signed main(){
int t;
cin>>t;
while(t--){
cin>>n;
int tmp = 3;
int now = 4;
while(n%tmp != 0){
tmp += now;
now *= 2;
}
cout<<n/tmp<<endl;
}
return 0;
}
B. Balanced Array
题意:找出一个数组,使得前一半元素都是偶数,后一半都是奇数。并且没有相同的元素。并且,前半部分的和等于后半部分的和。
思路:很容易想到,前面填充 2 4 6 8 10,后面填充1 3 5 7 9 这样子,但是这样子,两半和是不相等的。那么可以发现,如果这样填充的话, 后面的数比前面的每个小1,那么要让他们相等,就必须加上这个差值每个相差1,总的就是相差n/2。所以,如果n/2是奇数,因为后半部分也是奇数。那么他就会变成偶数。这就不符合题意了。所以,n/2是奇数的话,无解。反之,只要最后一个元素+n/2就行了。
AC代码:
#include <bits/stdc++.h>
#define int long long
#define mk make_pair
using namespace std;
const int N = 3e5+11;
const int mod = 1e9+7;
int t,n,m,k;
int a[N];
signed main(){
int t;
cin>>t;
while(t--){
cin>>n;
if(n%4 != 0){
cout<<"NO"<<endl;
}else{
for(int i = 0 ; i < n/2 ; i ++)
a[i] = i*2+2;
for(int i = n/2 ; i < n ; i ++)
a[i] = (i-n/2)*2+1;
a[n-1] += n/2;
cout<<"YES"<<endl;
for(int i = 0 ; i < n ; i ++){
cout<<a[i]<<" ";
}
cout<<endl;
}
}
return 0;
}
C. Alternating Subsequence
题意:一个数组,有正有负。然后要取一个子序列。子序列的元素正负号是交替出现的,求满足条件的最长的且和是最大子序列的和。
思路:要求最长,也就是碰到一堆连续的正数就取一个,碰到一堆连续的负数就取一个。并且都取最大的就好了。这样原数组中正负号交替出现了多少次,求出来的序列就出现了多少次。
AC代码:
#include <bits/stdc++.h>
#define int long long
#define mk make_pair
using namespace std;
const int N = 3e5+11;
const int mod = 1e9+7;
int t,n,m,k;
int a[N];
signed main(){
int t;
cin>>t;
while(t--){
cin>>n;
for(int i = 0 ; i < n ; i ++) cin>>a[i];
int pos = 1;
a[0] = a[0];
for(int i = 1 ; i < n ; i ++){
if(a[i]*a[pos-1] > 0){
a[pos-1] = max(a[pos-1],a[i]);
}else{
a[pos++] = a[i];
}
}
int sum = 0;
for(int i = 0 ; i < pos ; i ++) sum += a[i];
cout<<sum<<endl;
}
return 0;
}
D. Constant Palindrome Sum
题意:一个数组,a[i],a[n-i] 这样的两两为一对,他们的和为sum[i],然后给了一个k,数组的元素都小于k,并且可以任意改变数组元素的值,现在要求一个x,使得所有这样的对的sum都是x,并且改变元素的次数最小。输出最小次数。
思路:
心路历程:一开始想的是三分,调到了结束也没调出来。完事恍然大悟,三分是错的!明显不具有单调性。然后看了一些博客,发现都是分类+差分,怎么搜都是这么说,感觉抄来抄去,也没看懂。然后突然想到了线段树的做法。直接用线段树暴力搞就好了。AC了。 然后,发现,线段树维护区间信息不就和差分维护区间信息一样嘛。写题写傻了。
正式思路:首先用一颗线段树维护 [1 - 2k ] 的区间信息。初始全为0。其实记录的就是改成 x 需要的操作次数。因为需要区间操作所以用线段树维护。好,然后枚举所有的数对。对于一个数对 (a[i],a[n-i]),如果最后求的x == sum[i] 那么,这对数对需要的操作次数就是0。或者说,这个数对,对于 x,需要的操作是0。然后考虑。需要两次操作的情况。如果x 小于他们的最小值,那么两个数都得变吧。所以这时候操作次数是 2。这时候的区间就是 [1- min(a[i],a[j])],对于x属于这些区间,操作数为2。所以这时候就用到线段树了。把这个区间全加上2。另外一种需要2次操作的情况。就是,因为元素最大只能为k。如果 x > max(a[i],a[j])+k,那说明,即使把一个数改成了最大值k,依然不够,还得改另外一个数。所以他们的操作数是2。那么1次操作数的自然就夹在他们中间了。 也就是 [min+1 ~ max+k],只需要改变一个值就可以了,但是还要注意,sum也在这个区间里。对于x = sum 需要的操作次数是0。所以避免把sum也加 了就行。这时候可以发现,线段树仅仅维护了一个区间的单点信息,大材小用了。用差分维护是一样的一样的。
AC代码:
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 4e5 + 10;
//const int N = 1e6+7;
const int mod = 1e9+7;
int t,n,m,k;
int a[N],b[N];
typedef long long ll;
#define lson rt << 1 // == rt * 2 左儿子
#define rson rt << 1 | 1 // == rt * 2 + 1 右儿子
#define int_mid int mid = tree[rt].l + tree[rt].r >> 1
struct node {
int l, r;
ll val, lazy;
} tree[N * 4];
void push_up(int rt) {
//tree[rt].val = min(tree[lson].val, tree[rson].val);
//tree[rt].val = max(tree[lson].val, tree[rson].val);
tree[rt].val = tree[lson].val + tree[rson].val;
}
void push_down(int rt) {
if (tree[rt].lazy) {
tree[lson].lazy += tree[rt].lazy;
tree[rson].lazy += tree[rt].lazy;
//{ // 维护最大最小值
// tree[lson].val += tree[rt].lazy;
// tree[rson].val += tree[rt].lazy;
//}
{ // 维护和
int l = tree[rt].l, r = tree[rt].r;
int mid = l + r >> 1;
tree[lson].val += 1ll * (mid - l + 1) * tree[rt].lazy;
tree[rson].val += 1ll * (r - mid) * tree[rt].lazy;
}
tree[rt].lazy = 0;
}
}
void build(int rt, int l, int r) { // 建树
tree[rt].l = l, tree[rt].r = r;
tree[rt].lazy = 0;
if (l == r) {
tree[rt].val = 0; // 给定一个初始值
return;
} else {
int mid = l + r >> 1; // (l + r) / 2
build(lson, l, mid);
build(rson, mid + 1, r);
push_up(rt);
}
}
void update_point(int rt, int pos, ll val) { // 单点更新
if (tree[rt].l == tree[rt].r && pos == tree[rt].l) {
tree[rt].val += val;
return;
}
int_mid;
if (pos <= mid) update_point(lson, pos, val);
else update_point(rson, pos, val);
push_up(rt);
}
void update_interval(int rt, int l, int r, ll val) { // 区间更新
if (l <= tree[rt].l && r >= tree[rt].r) {
tree[rt].lazy += val;
//tree[rt].val += val; // 维护最大最小值
tree[rt].val += 1ll * (tree[rt].r - tree[rt].l + 1) * val; // 维护和
return;
}
push_down(rt);
int_mid;
if (l <= mid) update_interval(lson, l, r, val);
if (r > mid) update_interval(rson, l, r, val);
push_up(rt);
}
ll query_point(int rt, int pos) { // 单点查询
if (tree[rt].l == tree[rt].r && tree[rt].l == pos)
return tree[rt].val;
push_down(rt);
int_mid;
if (pos <= mid) return query_point(lson, pos);
else return query_point(rson, pos);
}
ll query_interval(int rt, int l, int r) { // 区间查询
if (l <= tree[rt].l && r >= tree[rt].r)
return tree[rt].val;
push_down(rt);
int_mid;
if (r <= mid) return query_interval(lson, l, r);
else if (l > mid) return query_interval(rson, l, r);
else {
//return min(query_interval(lson, l, mid), query_interval(rson, mid + 1, r));
//return max(query_interval(lson, l, mid), query_interval(rson, mid + 1, r));
return query_interval(lson, l, mid) + query_interval(rson, mid + 1, r);
}
}
signed main(){
int t;
cin>>t;
while(t--){
cin>>n>>k;
for(int i = 0 ; i < n ; i ++) cin>>a[i];
build(1,1,2*k+1);
for(int i = 0 ; i < n/2 ; i ++){
int sum = a[i]+a[n-i-1];
int minn = min(a[i],a[n-i-1]);
int maxx = max(a[i],a[n-i-1])+k;
update_interval(1,1,minn,2);
if(maxx>=minn+1){
update_interval(1,minn+1,maxx,1);
update_interval(1,sum,sum,-1);
}
update_interval(1,maxx+1,2*k+1,2);
}
int res = 1e18;
for(int i = 2 ; i <= 2*k ; i ++){
//cout<<i<<" "<<query_point(1,i)<<endl;
res = min(res,query_point(1,i));
}
cout<<res<<endl;
}
return 0;
}
E. Weights Distributing
题意:给定一个无向图。给定一个权值数组。要把权值分配到每条边上,使得从a到b再到c经过的总边权和最小。
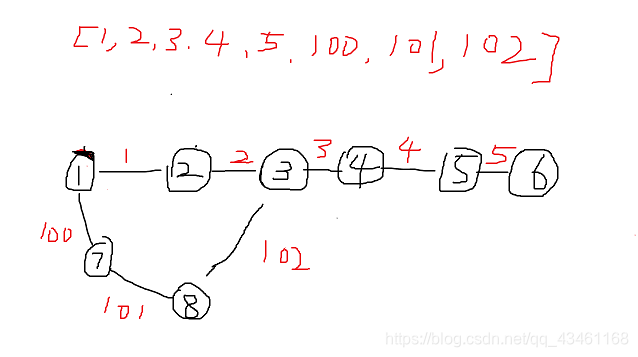
思路:显然,把最小的权值分配到最短路径上就是最优解。考虑一个朴素的想法。就是先求a-b的最短路径。然后把小权值分配上去。再求b-a的最短路径,把剩下最小的边权分配上去。但是这样肯定是不对的。如下图:这种策略下,如果要从6到1再到8。那么肯定不会选择到 3 -> 8这条边。 但是实际上,如果绕远路从 1-2-3-8 实际上会比 1-7-8 更优。所以不能直接这样贪心。 有可能有的边会走两遍。那就要去枚举,哪些边会走两遍,或者说枚举哪些点作为中继点,也就是说 a-d-b-d-c。枚举这个d。那么这个d肯定是在某一条最短路径上的点。所以要先找出所有 可能在最短路径上的点。然后以这些点作为中继。但是还要枚举两遍。有可能是在 a-b 的最短路径上的点作为中继。也有可能是 b-c最短路径上的点作为中继。取最小。才是正确答案。
AC代码:
#include <iostream>
#include <bits/stdc++.h>
#define int long long
#define mk make_pair
#define gcd __gcd
#define pb push_back
using namespace std;
const double eps = 1e-10;
const int mod = 1e9+7;
const int N = 1e6+7;
int n,m,k,t = 1,cas = 1;
//int a[N],b[N];
struct node{
int from,to,dis;
node(int a,int b,int c):from(a),to(b),dis(c){}
};
vector<node> que;
int dis1[N];
int dis2[N];
int cost[N];
int onpath[N];
bool mark[N];
vector<int> edge[N];
void bfs(int s,int t,int dis[]){
for(int i = 0 ; i <= n ; i ++) mark[i] = 0;
mark[s] = 1;
int pos = 0;
que.pb(node(-1,s,0));
while(pos < que.size()){
node now = que[pos++];
dis[now.to] = now.dis;
for(int i = 0; i < edge[now.to].size();i ++){
int to = edge[now.to][i];
if(!mark[to]){
mark[to] = 1;
que.pb(node(pos-1,to,now.dis+1));
}
}
}
que.clear();
}
int solve(int a,int b,int c){
for(int i = 1 ; i <= n ; i ++)
onpath[i] = 0;
bfs(a,b,dis1);
int dis_ab = dis1[b];
bfs(b,a,dis2);
for(int i = 1 ; i <= n ; i ++)
if(dis1[i]+dis2[i] == dis_ab)
onpath[i] = 1;
bfs(c,b,dis2);
int res = cost[dis_ab];
int minn = 1e18;
for(int i = 1; i <= n; i ++){
if(!onpath[i]) continue;
if(dis1[i] > dis_ab) continue;
if(dis2[i]+dis_ab > m) continue;
int new_cost = cost[dis_ab-dis1[i]] + (cost[dis2[i]+dis_ab]-cost[dis_ab]);
//cout<<i<<" "<< dis1[i]<<" "<<dis2[i]<<" "<<(cost[dis2[i]+dis_ab]-cost[dis_ab])<<" "<<new_cost<<endl;
minn = min(minn,new_cost);
}
return res+minn;
}
signed main(){
cin>>t;
while(t--){
int a,b,c;
cin>>n>>m>>a>>b>>c;
for(int i = 1 ; i <= n ; i ++)
edge[i].clear();
for(int i = 1 ; i <= m ; i ++) cin>>cost[i];
sort(cost+1,cost+m+1);
for(int i = 2 ; i <= m ; i ++)
cost[i] += cost[i-1];
for(int i = 0 ; i < m ; i ++){
int x,y;
cin>>x>>y;
edge[x].pb(y);
edge[y].pb(x);
}
cout<<min(solve(a,b,c),solve(c,b,a))<<endl;
}
}
/**
**/
版权声明:本文为qq_43461168原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。