484-红黑树 – 源码巴士

1、红黑树和AVL树的区别

AVL树是一棵平衡树，为了维护节点平衡引入4种旋转操作。
任意节点的左右子树高度差不会超过1；
平衡的好处是：从根节点到每个叶子结点的访问的路径是相当的，查询的效率非常高。
但是删除节点，AVL树可能从当前失衡节点开始，向根节点一直要进行回溯，都有可能发生失衡，最差情况全部失衡，都需要进行节点的旋转操作，节点的旋转次数是和树的高度有关的O(logn)。
对于插入节点，因为都是插入在叶子节点上，最多旋转2次，最少就旋转1次（左平衡或者右平衡旋转）。

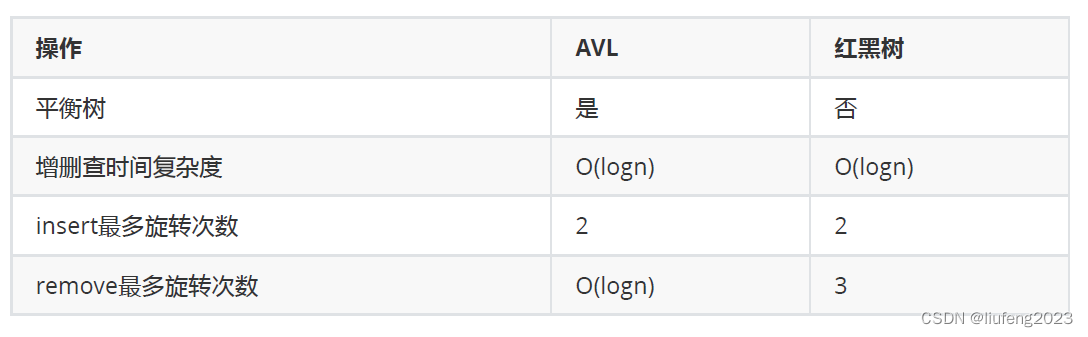
在这里插入图片描述
红黑树：

红黑树不是一棵平衡树（没有要求节点必须平衡），节点的左右子树高度差，长的不超过短的2倍。
效率上比AVL树好一些。节点的旋转的次数比AVL树少很多；（AVL树可能从当前失衡节点开始，向根节点一直要进行回溯，都有可能发生失衡，最差情况全部失衡，都需要进行节点的旋转操作，节点的旋转次数是和树的高度有关的O(logn)。）
但是增加了节点的着色。

红黑树和AVL树的对比：

如果只做插入和查询，我们肯定选择AVL树，因为AVL是绝对平衡的树，查询效率高于红黑树。
如果要做插入，删除和查询，都比较多，我们选择红黑树。
数据量小的情况下（几十万，几百万），两者差别不大。
数据量大的情况下（上千万），红黑树效率比较好！(平衡二叉树1000万的数据大概是24层)

C++的STL的map和set用红黑树，因为要增，删，查，这些操作都比较多。

2、红黑树的性质

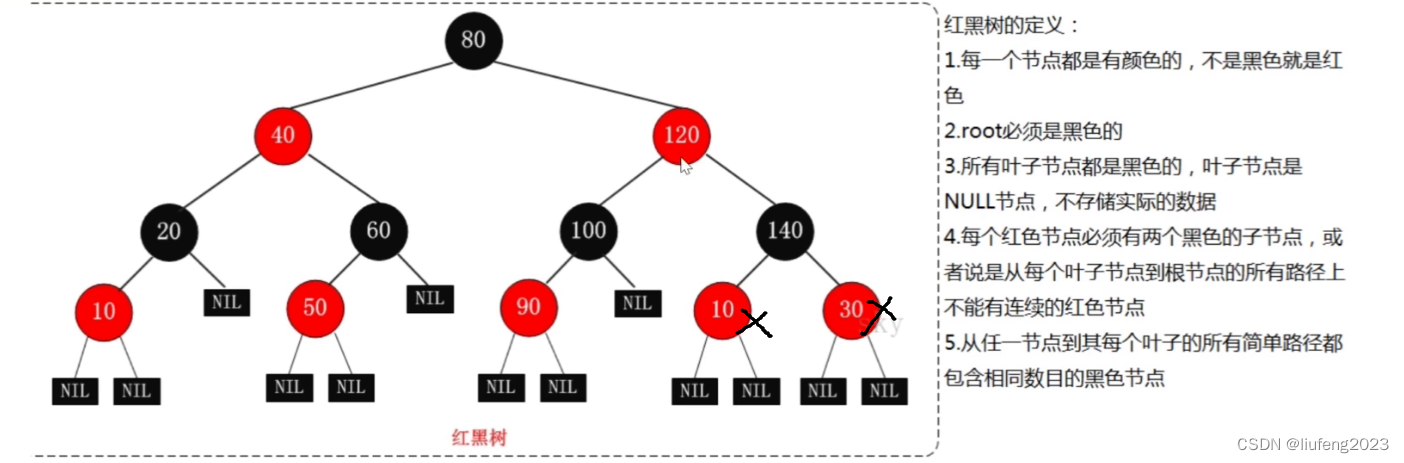
在这里插入图片描述

红黑树也是一棵二叉搜索树。 满足每个节点的左子树的值都小于节点的值，节点的值都小于节点的右子树的值。（上面画的10和30不准确）

红黑树的5个性质：

红黑树的每一个节点都有颜色，不是黑色就是红色。
叶子节点的左右孩子都是黑色，因为都为空的。空nullptr就是黑色。
根节点root必须是黑色。
不能出现连续的红色节点，父亲是红色，孩子不能是红色，孩子只能是黑色。如果孩子有红色节点，父亲不能是红色节点。
从根节点到任意一个叶子节点的路径上，黑色节点的数量必须是一致的。

我们在进行插入和删除中，以上性质必须维持着！！！

面试问题：在红黑树中，节点的左右子树的高度差最多不能超过多少？

根节点root分别到叶子节点1, 2，假设下面这种极端的情况：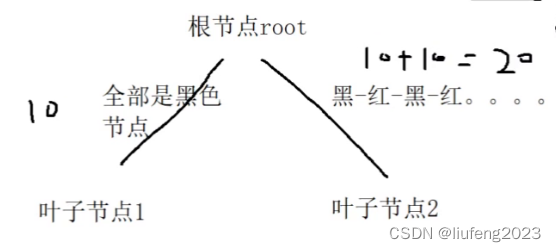
在这里插入图片描述

根节点到叶子节点1的路径上全部是黑节点；
根节点到叶子节点2的路径上的黑色节点和根节点到叶子节点1的路径上黑节点相等；但是它是最差情况，也就是黑红交替，就是左边的2倍了！

所以在红黑树中，长的最多不能超过短的2倍。

3、红黑树的插入操作的理论

我们还是按照BST树的插入方式进行的：只是增加了条件（需要满足红黑树的5个性质）：

如果是空树 ，插入的话，节点肯定是黑色的，因为是根节点！
如果树非空，我们插入的节点就都是叶子节点：
- 如果插入的是黑色节点，这条路径上的黑色节点数量就增加1了，红黑树性质就被打破了；
- 所以，我们只能插入红色节点！！！但是红色不能连续哦！！！所以我们此时要检查父节点的颜色：
  - 如果父节点是黑色，就不用做任何其他调整，直接插入红色节点；
  - 如果父亲是红色节点，造成连续的红色节点，我们进行插入的调整如下：

如果父亲是红色节点，造成连续的红色节点，我们进行插入的调整如下：

情况1

叶子节点的局部树 的图如下：

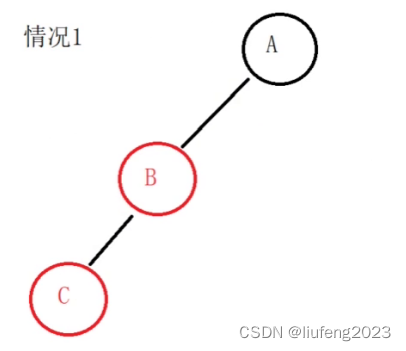
在这里插入图片描述
我们要新插入节点C，红色，但是父节点B也是红色，所以现在不满足红黑树的性质。

要进行调整：

把B的颜色和它的父亲A的颜色交换一下！
A变红色，B变黑色。C还是红色的C。

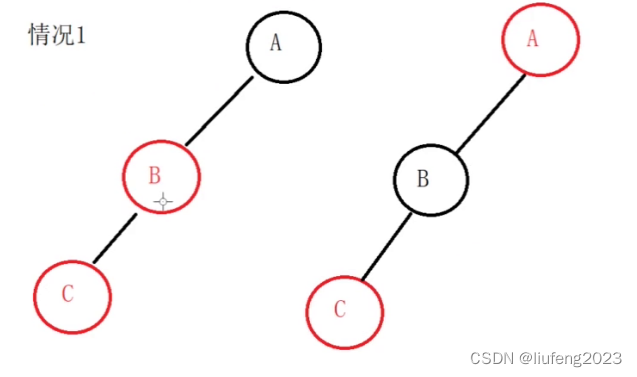
但是这样并不好，因为你还有叔叔呢！

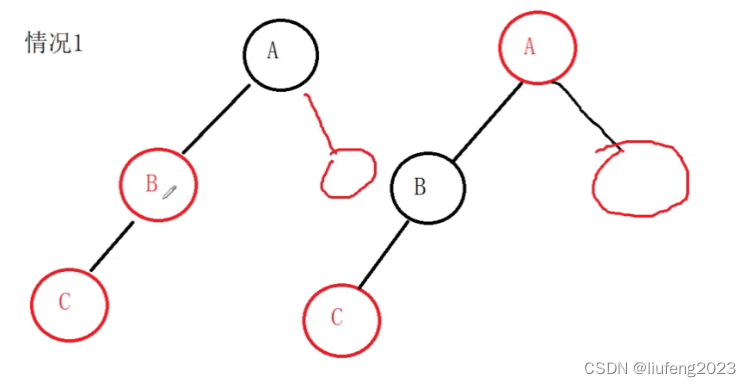
在这里插入图片描述
这样，又产生连续红色的节点了！！！我们在插入的前提还要看看叔叔！！！

有叔叔的情况1：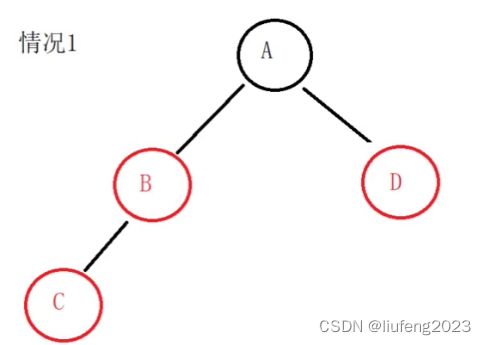
在这里插入图片描述
我们插入了一个C节点，连续的红色节点出现了，现在打算把父亲B的颜色和爷爷A的颜色交换，但是如果爷爷A是红色，和叔叔D就是连续红色了。

我们在插入C，发现其父亲B和叔叔D都是红色，我们把爷爷A的颜色改为红色，父亲B的颜色改为黑色，把叔叔D的颜色改为黑色。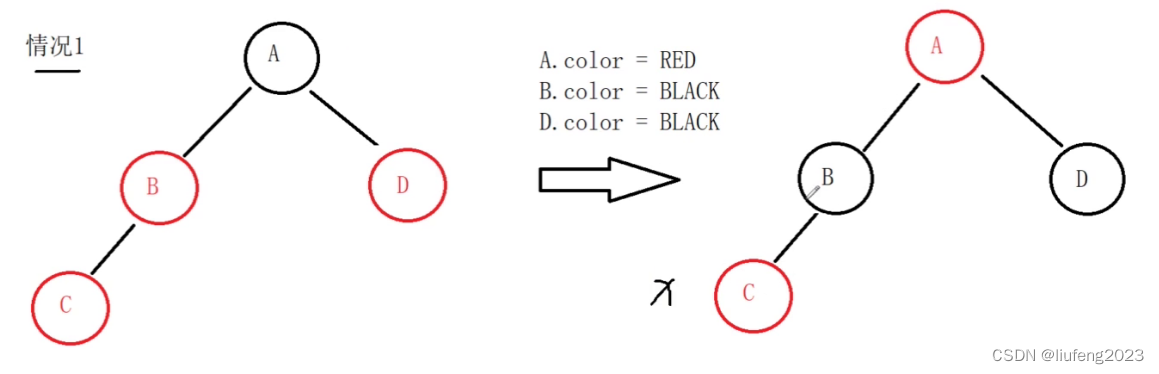
在这里插入图片描述
上图不是完全的红黑树，只是局部的，从局部来看，已经没有出现连续的红色节点，A往左右走也都是1个黑色节点。

但是爷爷A的父亲有可能是黑色，也有可能是红色哦！
x是新插入的节点C
调整后，我们让x指向A，
然后继续向上回溯调整，和刚才一样的方式！

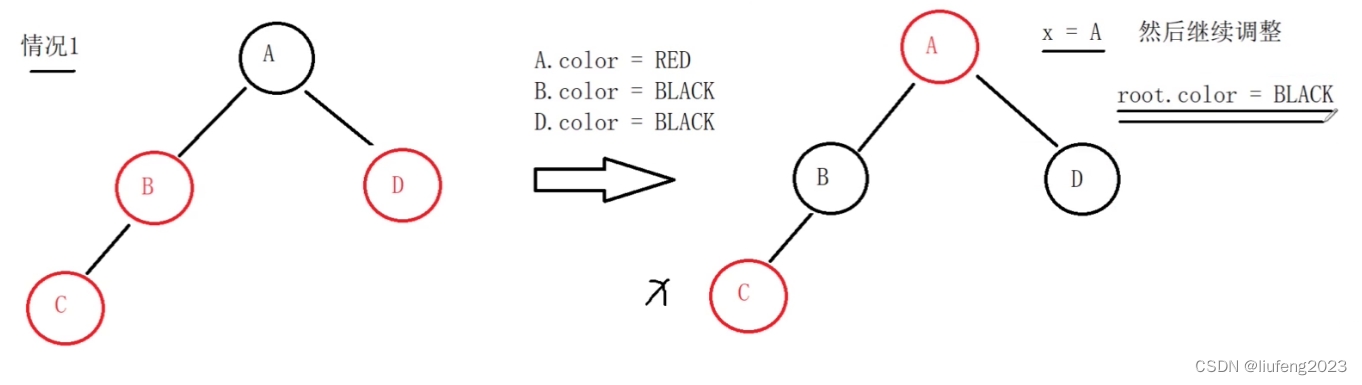
在这里插入图片描述

但是，根节点的颜色必须强制为黑色！！！

情况2

插入节点C的叔叔节点是黑色的。
此时就不能把父亲节点的颜色和爷爷节点的颜色交换了。

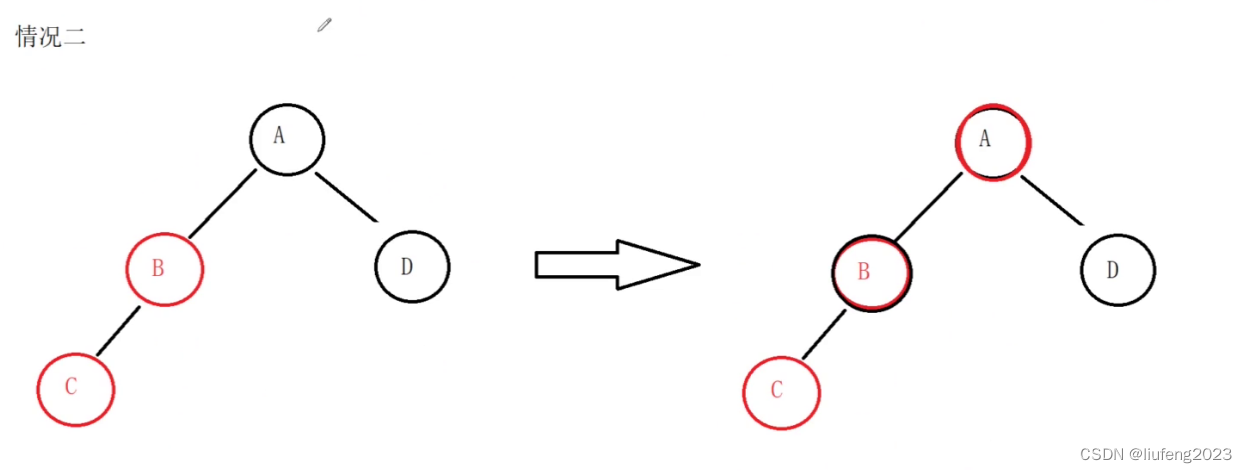
在这里插入图片描述
实际上，上图的操作是不行的。

从上往下，沿着根节点的某一个路径，原来经过A到左边1个黑色，经过A右边2个黑色，经过交换颜色后，现在经过A到右边就只有1个黑色了！！！

黑色节点的数量就不符合性质了。

我们应该：
原来黑色的A是左右两边的公共节点，它对左右两个局部路径都增加1个黑色的数量，现在把A涂成红色，很明显，往右走，就少了1个黑色节点了。

但是我们再多做1步操作就可以了：
C的父亲与爷爷交换颜色后，以A为轴，右旋转一下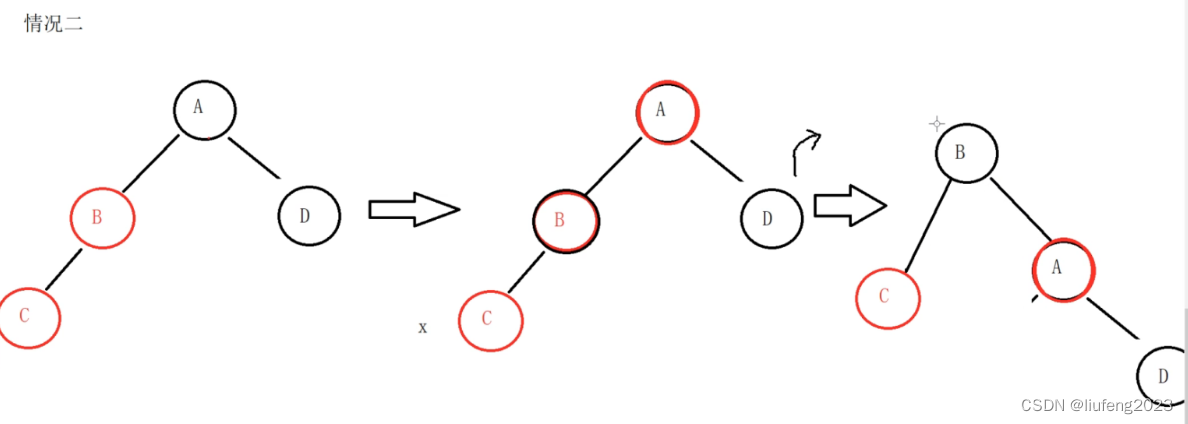
在这里插入图片描述
这样就OK了！！！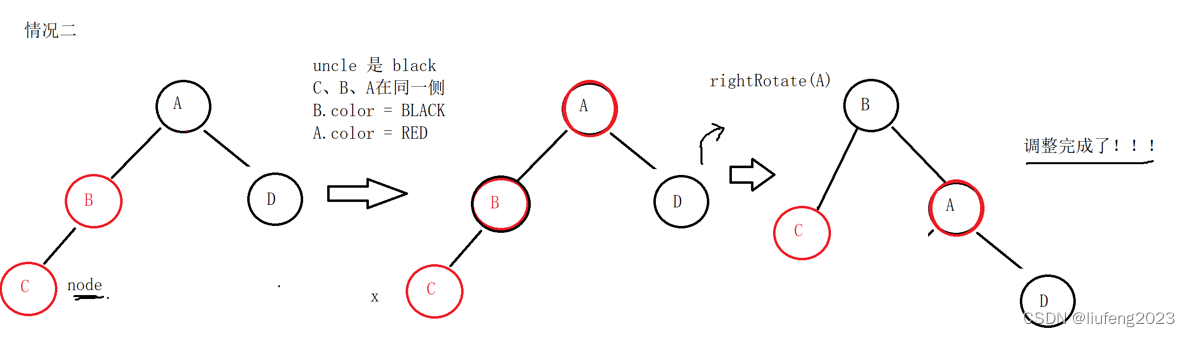

情况3

插入的C节点没有和父亲B，爷爷A在同一个方向上。

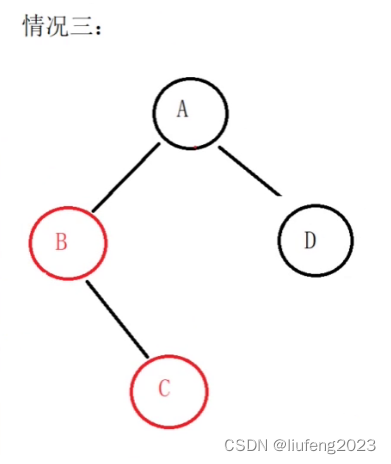
在这里插入图片描述
如果把C的父亲B的颜色和爷爷A的颜色一交换，然后A为轴右旋转一下，行不行？

不行！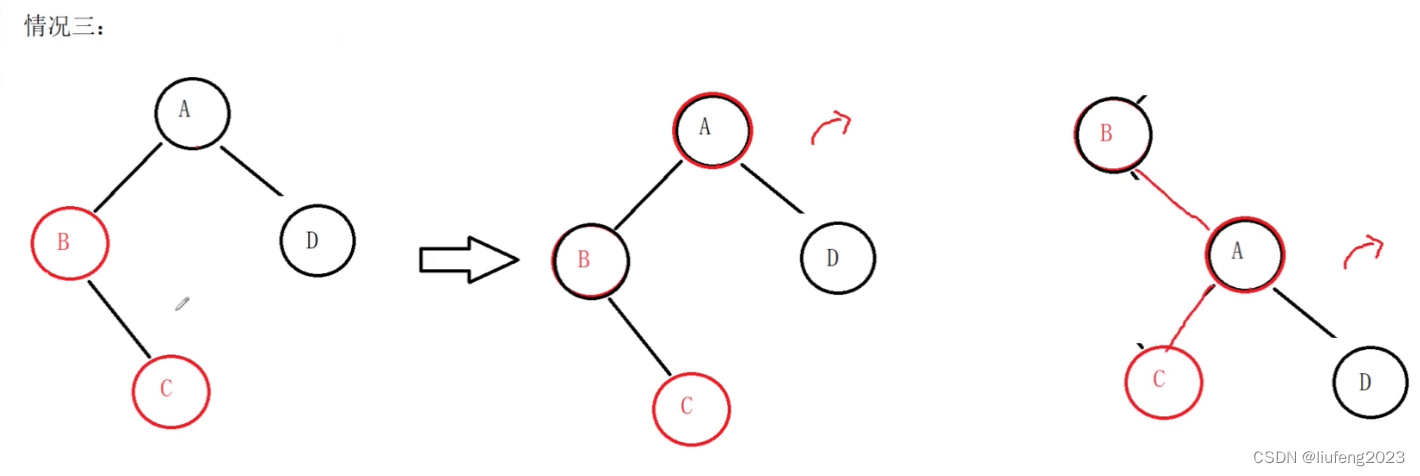
在这里插入图片描述
A和C还是连续的红色了。

这样解决不了问题！

我们得学学情况2的思想：

首先把C和C的父亲节点B和C的爷爷节点A掰到同一条线上。
首先以B为轴，做一个左旋转操作。

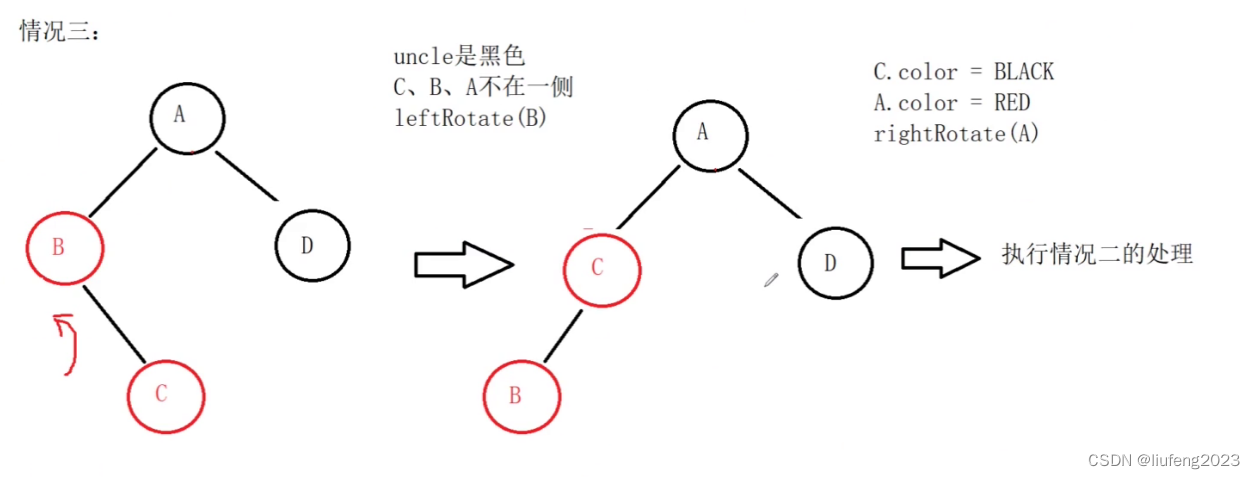
在这里插入图片描述

4、红黑树的定义代码

在红黑树中，访问节点的时候，要访问到它的父亲，爷爷和叔叔。
包括删除，还要访问它的兄弟节点。

在递归的过程中就不方便了，而且对于红黑树来说，插入操作最多旋转2次，局部解决完之后，局部没有改变红黑树的性质，全局自然就维护了红黑树的性质，局部解决好了，就不用向上回溯了，所以我们不需要使用递归，递归的话要从插入的地方回溯到根节点，浪费效率。

5、封装接口的代码

6、红黑树的左旋转和右旋转代码

红黑树中只有左旋和右旋，没有左平衡和右平衡！

左旋转

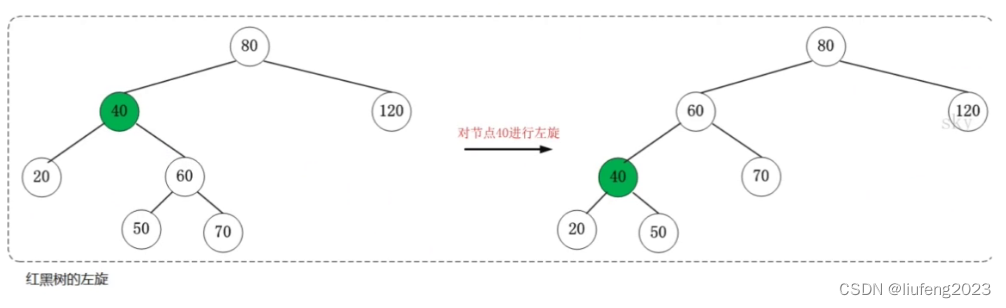
在这里插入图片描述

//左旋转
void leftRotate(Node* node)
{
	Node* child = node->right_;
	child->parent_ = node->parent_;
	if (node->parent_ == nullptr)
	{
		//node本身就是root节点
		root_ = child;//child变成根节点了
	}
	else//node的父节点不为空
	{
		if (node->parent_->left_ == node)//node在父节点的左孩子
		{
			node->parent_->left_ = child;
		}
		else//node在父节点的右孩子
		{
			node->parent_->right_ = child;
		}
	}

	node->right_ = child->left_;
	if (child->left_ != nullptr)
	{
		child->left_->parent_ = node;
	}

	child->left_ = node;
	node->parent_ = child;
}

右旋转

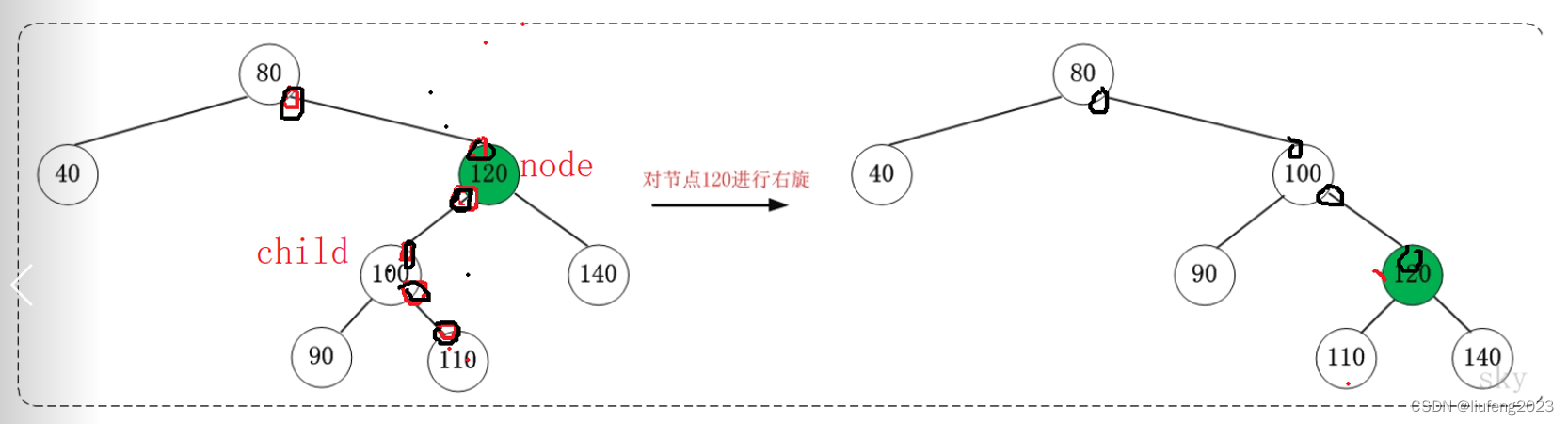
在这里插入图片描述

//右旋转
void rightRotate(Node* node)
{
	Node* child = node->left_;
	child->parent_ = node->parent_;
	if (node->parent_ == nullptr)
	{
		//node原来就是root节点
		root_ = child;
	}
	else
	{
		if (node->parent_->left_ == node)
		{
			//node在父节点的左边
			node->parent_->left_ = child;
		}
		else
		{
			//node在父节点的右边
			node->parent_->right_ = child;
		}
	}

	node->left_ = child->right_;
	if (child->right_ != nullptr)
	{
		child->right_->parent_ = node;
	}

	child->right_ = node;
	node->parent_ = child;
}

7、红黑树的插入操作代码

//插入操作
void insert(const T& val)
{
	if (root_ == nullptr)
	{
		root_ = new Node(val);//刚好默认是黑色
		return;
	}

	Node* parent = nullptr;
	Node* cur = root_;
	while (cur != nullptr)
	{
		if (cur->data_ > val)//当前节点的值大于要插入的值
		{
			parent = cur;
			cur = cur->left_;
		}
		else if (cur->data_ < val)//当前节点的值小于要插入的值
		{
			parent = cur;
			cur = cur->right_;
		}
		else//值存在，不插入重复的值
		{
			return;
		}
	}

	//设置当前节点的parent和颜色
	Node* node = new Node(val, parent, nullptr, nullptr, RED);//新节点设置成红色
	if (parent->data_ > val)
	{
		parent->left_ = node;//插在父亲的左孩子域
	}
	else
	{
		parent->right_ = node;//插在父亲的右孩子域
	}

	//如果新插入的红色节点，父节点也是红色，不满足红黑树性质，进行插入调整操作
	if (RED == color(parent))
	{
		fixAfterInsert(node);
	}
}

//红黑树的插入调整操作
void fixAfterInsert(Node* node)
{
	//如果当前红色节点的父节点也是红色，继续调整
	while (color(parent(node)) == RED)
	{
		if (left(parent(parent(node))) == parent(node))//爷爷节点的左孩子是我的父亲
		{
			//表示插入的节点在左子树当中，叔叔在右边，插入要看叔叔
			Node* uncle = right(parent(parent(node)));//叔叔在爷爷的右孩子
			if (RED == color(uncle))//情况一，叔叔节点也是红色
			{
				setColor(parent(node), BLACK);
				setColor(uncle, BLACK);
				setColor(parent(parent(node)), RED);
				node = parent(parent(node));//node指向他的爷爷，继续调整上去
			}
			else//叔叔节点是黑色
			{
				//先处理情况三，插入的节点和父亲，爷爷不在一侧
				if (right(parent(node)) == node)
				{
					node = parent(node);
					leftRotate(node);
					//进行左旋转，node此时指向的就是情况二中的左边最后一个节点的位置
				}

				//统一处理情况二
				setColor(parent(node), BLACK);
				setColor(parent(parent(node)), RED);
				rightRotate(parent(parent(node)));//右旋转
				break;//调整已经完成
			}
		}
		else//插入的节点在右子树当中
		{
			Node* uncle = left(parent(parent(node)));
			if (RED == color(uncle))//情况一
			{
				setColor(parent(node), BLACK);
				setColor(uncle, BLACK);
				setColor(parent(parent(node)), RED);
				node = parent(parent(node));//继续调整
			}
			else
			{
				//先处理情况三
				if (left(parent(node)) == node)
				{
					node = parent(node);
					rightRotate(node);
				}

				//统一处理情况二
				setColor(parent(node), BLACK);
				setColor(parent(parent(node)), RED);
				leftRotate(parent(parent(node)));
				break;//调整已经完成
			}
		}
	}

	//此处强制root为黑色节点
	setColor(root_, BLACK);
}

8、插入代码功能测试（插入1-10测试）

1、发现23是连续的红色节点；（插入的节点就是红色的）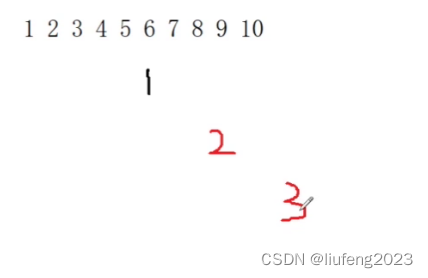
在这里插入图片描述
这属于我们情况2的镜像情况：（这里的叔叔其实没有，也是黑色）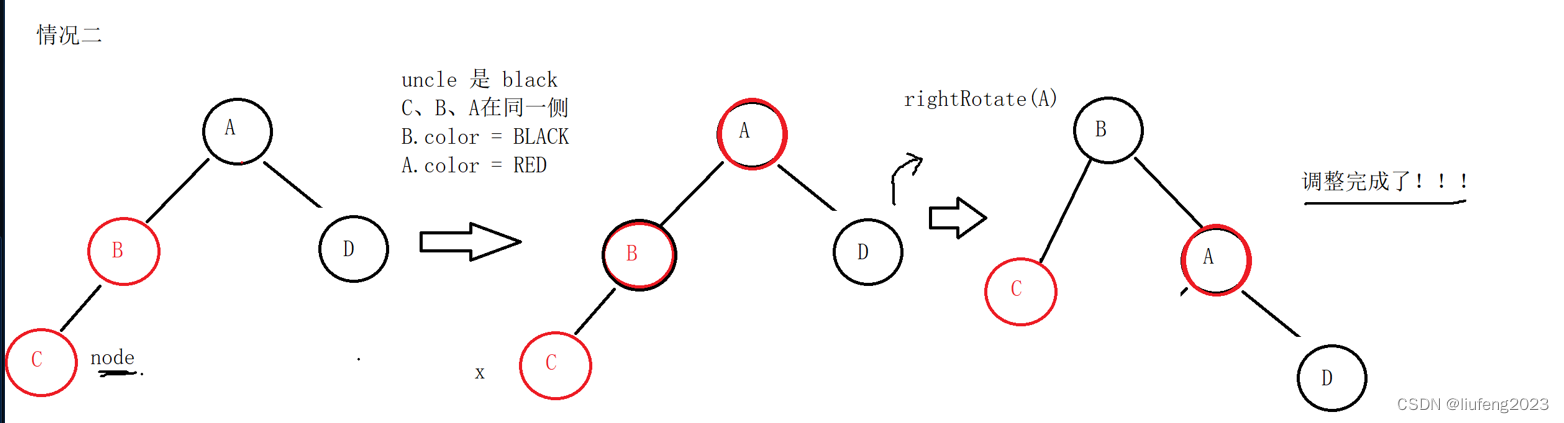

将插入节点的父节点变为黑色，将爷爷节点变为红色，并且以爷爷节点做左旋操作！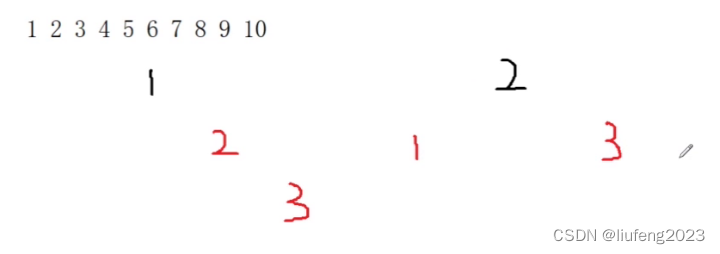

2、再插入4，34都是红色，不满足性质，看叔叔，红色；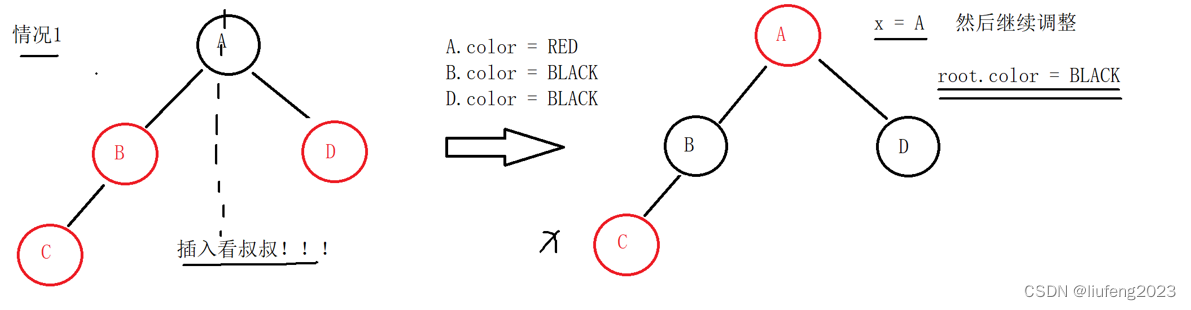
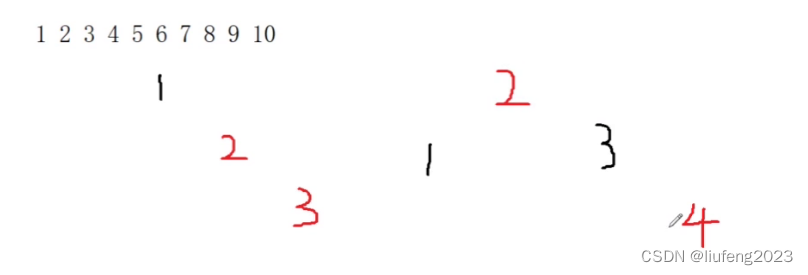
在这里插入图片描述

此时2变红了，还需要以2继续向上调整。2的父亲是空，此时我们跳出循环，将2置为黑色，因为它是根节点！

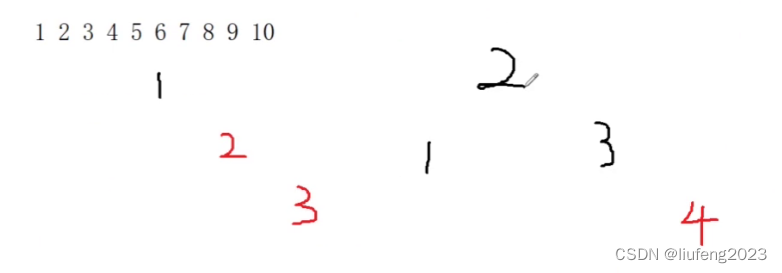
在这里插入图片描述
3、继续插入5，45不满足性质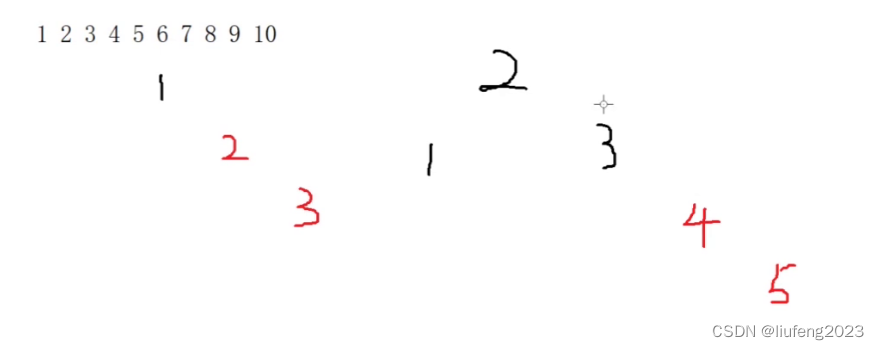

看叔叔，叔叔没有，在3的左侧，没有就是黑色，黑色就是情况2；

将5的父节点4变为黑色，爷爷3变为红色，以5的爷爷节点4作为根节点进行左旋转（只对345进行左旋转）；

4、插入6，56都是红色节点，不满足性质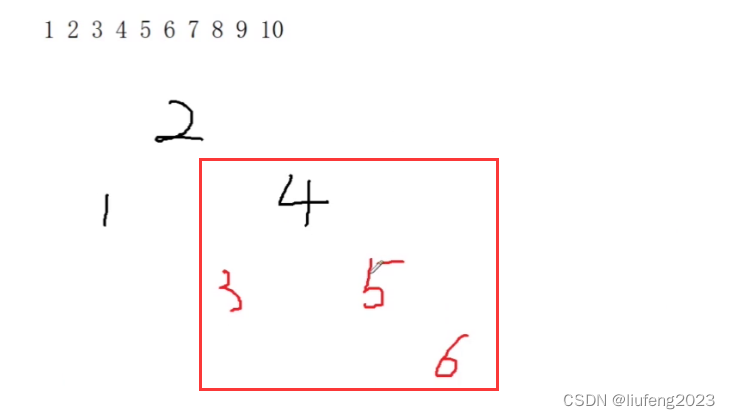
在这里插入图片描述
对应情况1；
将父亲和叔叔3和5变为黑色，将爷爷4变为红色；
再到4进行相同操作，4的父节点为黑色，满足性质，退出！

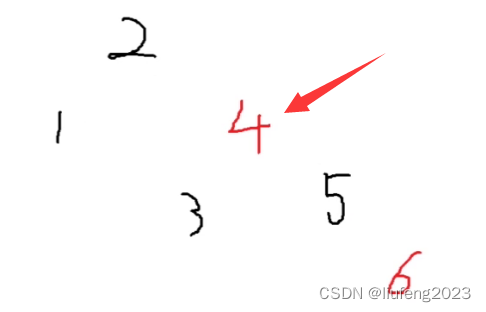
在这里插入图片描述
5、插入7，67不满足性质；

5的左边为叔叔节点，为黑色，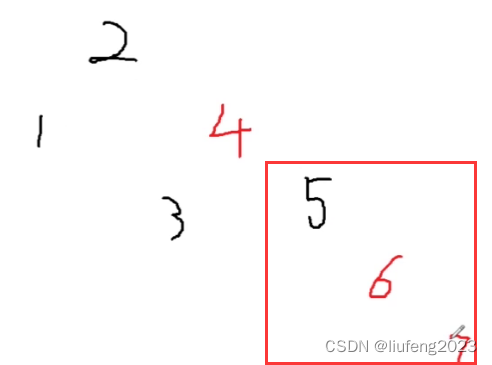
在这里插入图片描述
对应情况2：

将父节点6变为黑色，将爷爷节点5变为红色，以5进行左旋：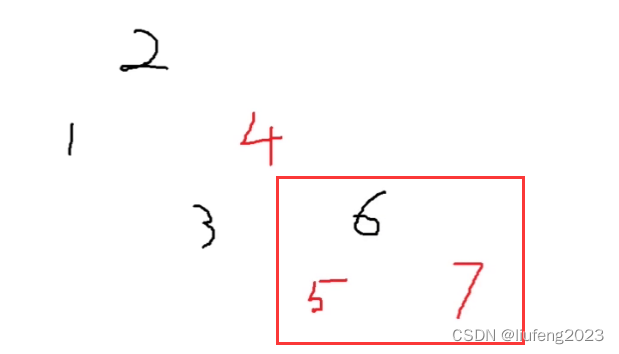

我们也可以发现红黑树不是一个平衡树！

6、插入8，78红色，不满足红黑树的性质；

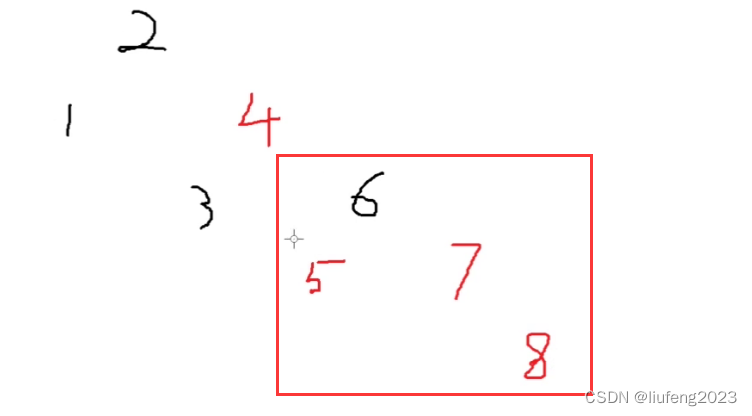
在这里插入图片描述
看叔叔5，红色，满足情况1；

将父节点5和叔叔节点7变为黑色，将爷爷6变为红色；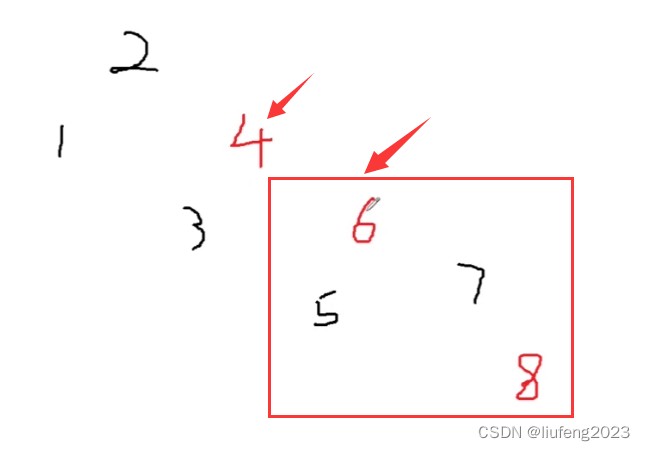

此时发现4和6都是红色，不满足性质，将节点指向爷爷6，继续向上调整；

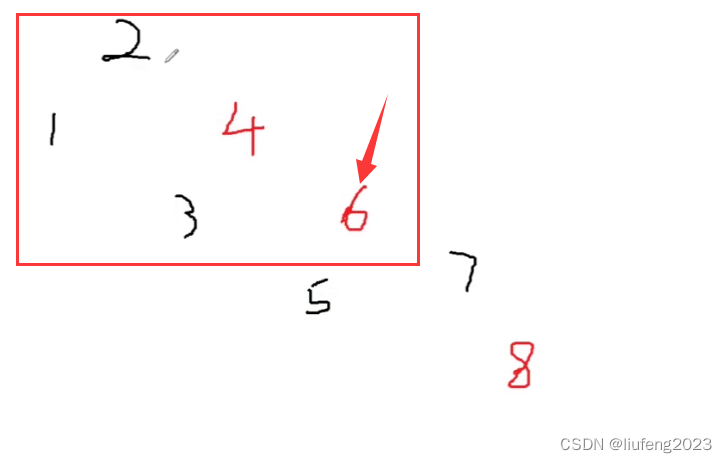
在这里插入图片描述
此时叔叔节点为1，黑色，且4和6在同一侧，对应情况2；
将父节点4和爷爷节点2将颜色换下，在以爷爷2节点进行左旋转：

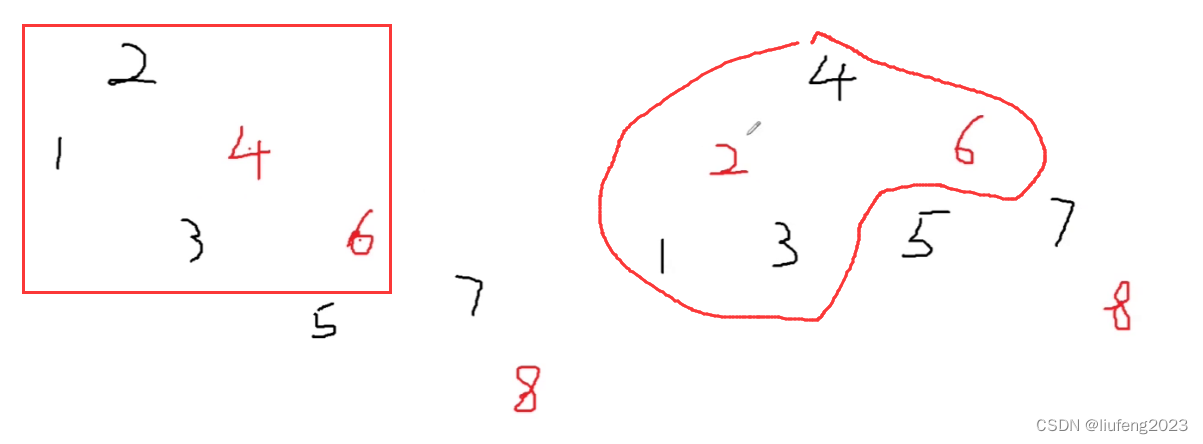
在这里插入图片描述

7、插入9，89不满足性质；

9的叔叔节点没有，默认是黑色；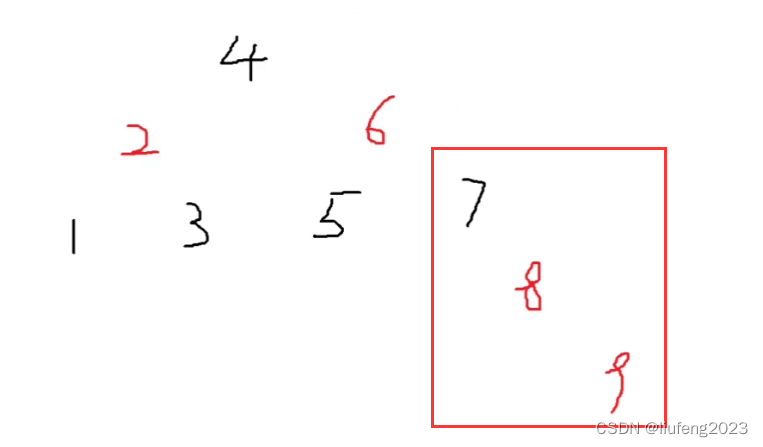
在这里插入图片描述
满足情况2；

将9的父节点变为8变为黑色，将爷爷节点7变为红色，以爷爷节点7进行左旋转；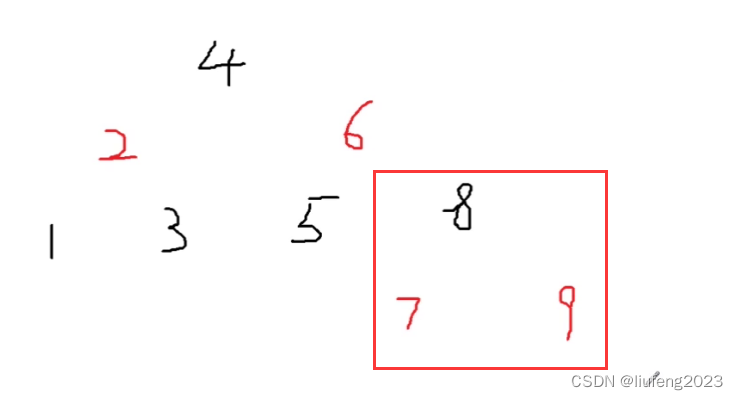

8、插入10，910不满足二叉树的性质；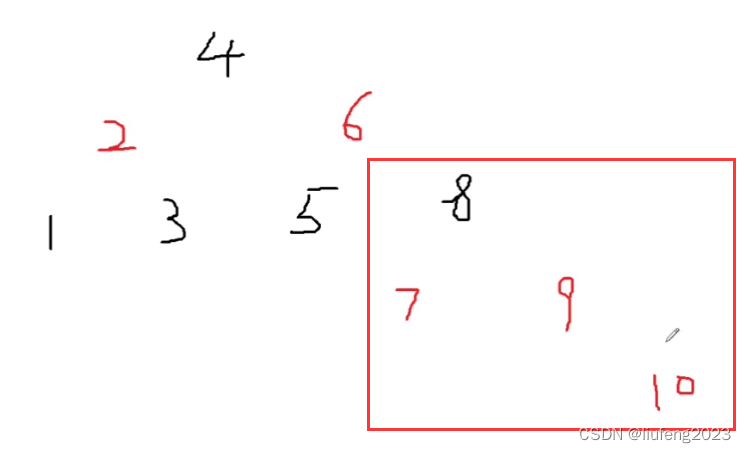
在这里插入图片描述
对应情况1；
将父节点和叔叔节点变为黑色，将爷爷节点变为红色；

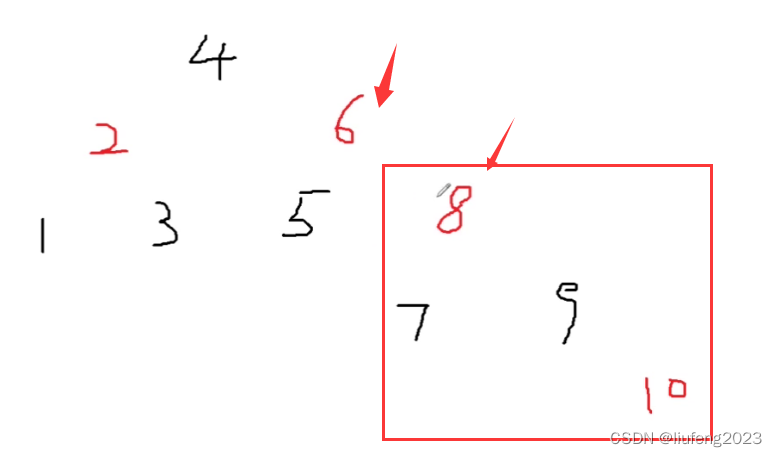
在这里插入图片描述
此时68变为红色，不满足性质，将节点指向爷爷节点8，继续调整：

此时叔叔2为红色，对应情况1，将叔叔2和父亲6都置为黑色，再将爷爷节点4置为红色;

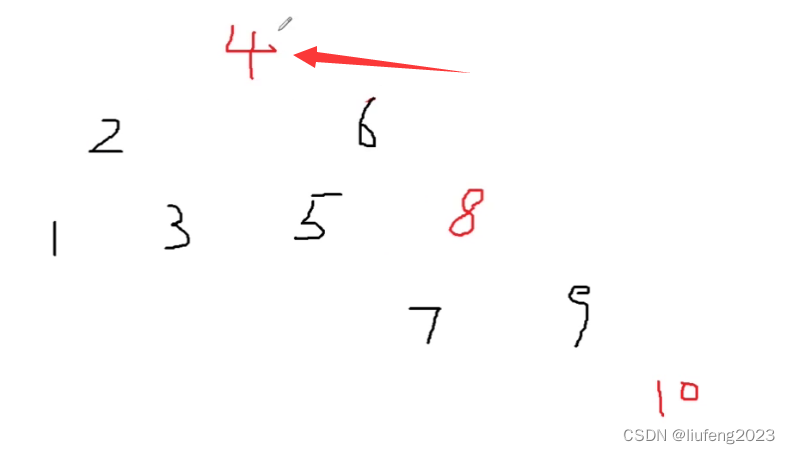
在这里插入图片描述
再将节点指向爷爷节点4，继续向上操作，发现4的父节点为空，4是根节点，跳出循环，将根节点4置为黑色！

最终结果：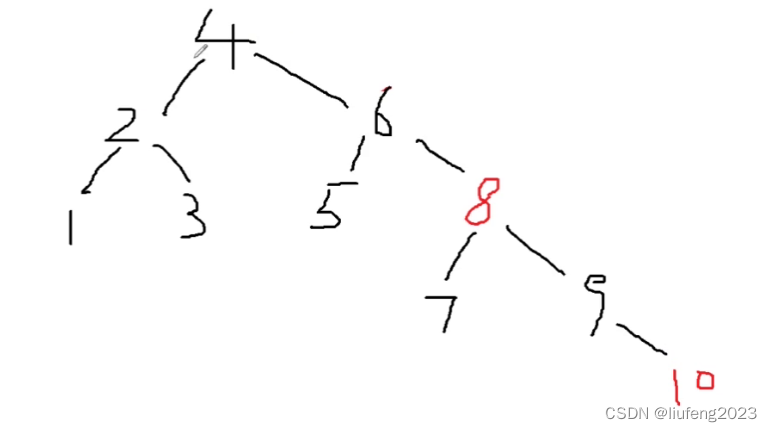
在这里插入图片描述

int main()
{
	RBTree<int> rb;
	for (int i = 1; i <= 4; ++i)
	{
		rb.insert(i);
	}

	return 0;
}

9、红黑树的删除理论

删除一个节点：

如果是有2个孩子的节点删除，转换成----前驱节点的删除—删除的节点最多有1个孩子。

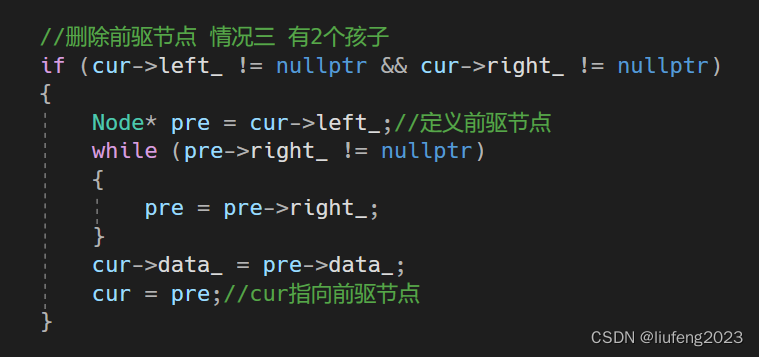
1、如果删除的是1个红色节点（父亲和孩子肯定是黑色），不影响该路径上黑色节点的数量，都不会破坏红黑树的性质，所以不做任何删除的调整工作。

2、如果删除的是1个黑色节点，孩子要补上去，占据它原来的位置；

分2种情况：

如果补上来的孩子是红色节点，直接把这个孩子涂成黑色，调整完成！！！
如果补上来的孩子是黑色节点，那在当前的路径上没办法再补一个黑色节点出来了。只能从兄弟那里借调黑色节点了。
分成4种情况：
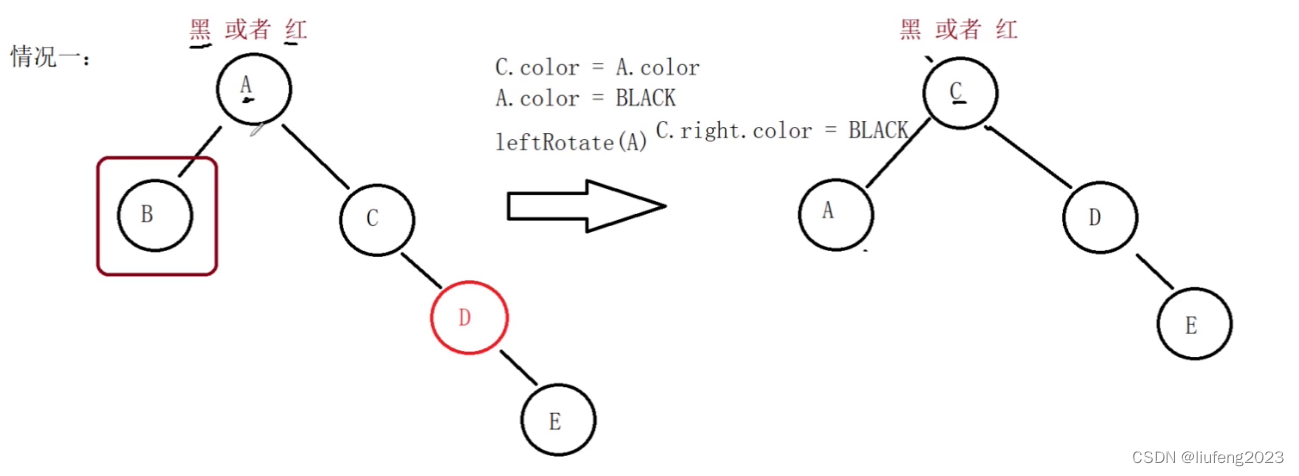
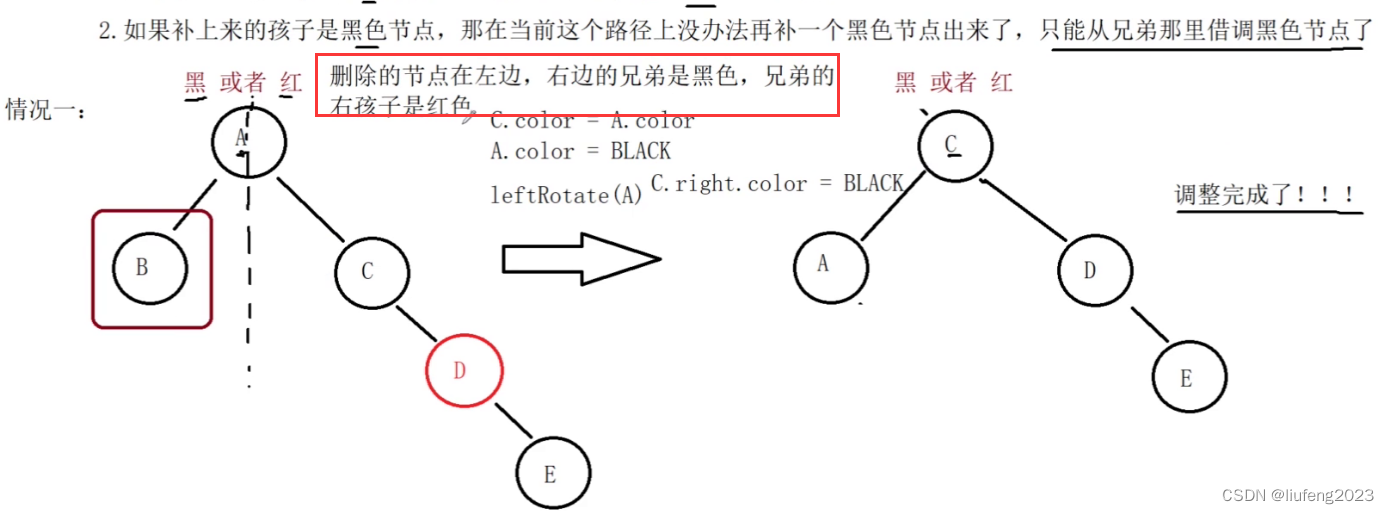
我们画的是局部的。
情况1：
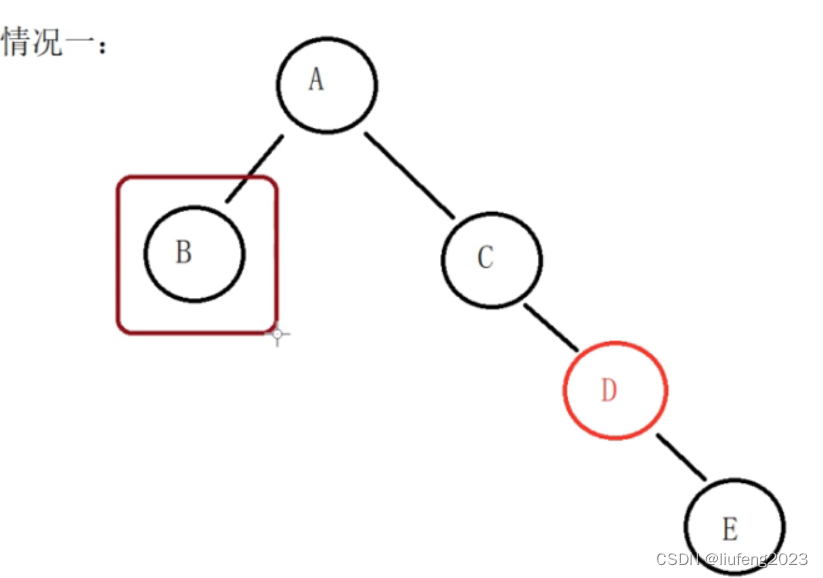
我们现在要删除B节点，B以及B的孩子是黑色的。
删除B后，要从兄弟借黑色节点，首先兄弟本身就得是黑色。其次，兄弟的孩子也得是红色。我们把兄弟的孩子的红色补成黑色。我们把C的黑色拿到左边来。
父节点A有可能是红也有可能是黑。我们这么调整：

情况2：

我们要删除B节点，但是兄弟节点是黑色的，但是红色节点不在兄弟的右孩子，在兄弟的左孩子。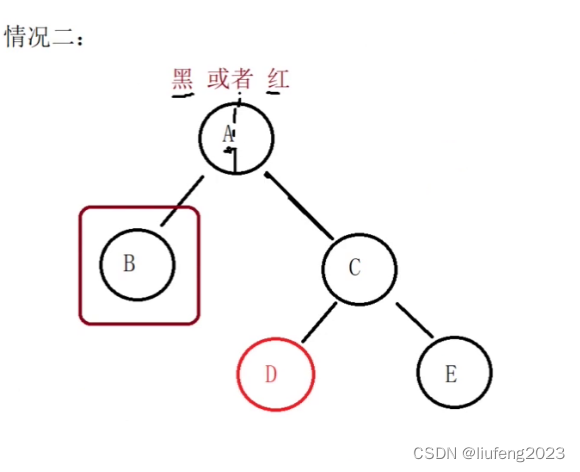
在这里插入图片描述

如果我们以A节点进行左旋转的话：
旋转的时候，我们又不能让D跑到左子树这边上去了。我们要保证的是兄弟的右孩子是红色的，然后才能补上黑色，补齐黑色的个数。

所以我们要处理的是：

第一步：以兄弟节点C为轴进行右旋转操作。这样就转成情况1了！

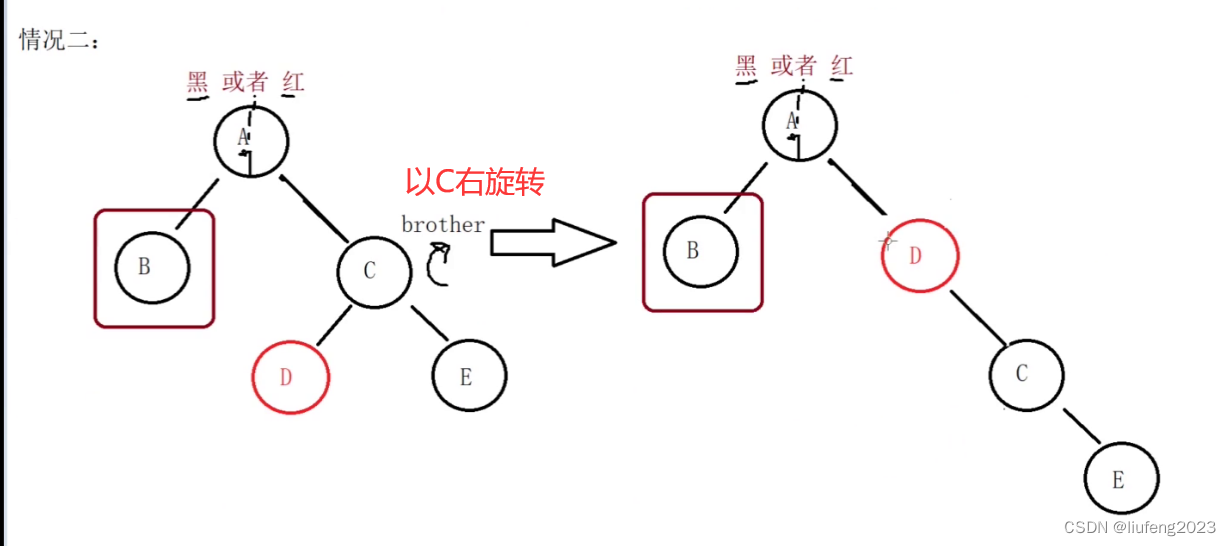
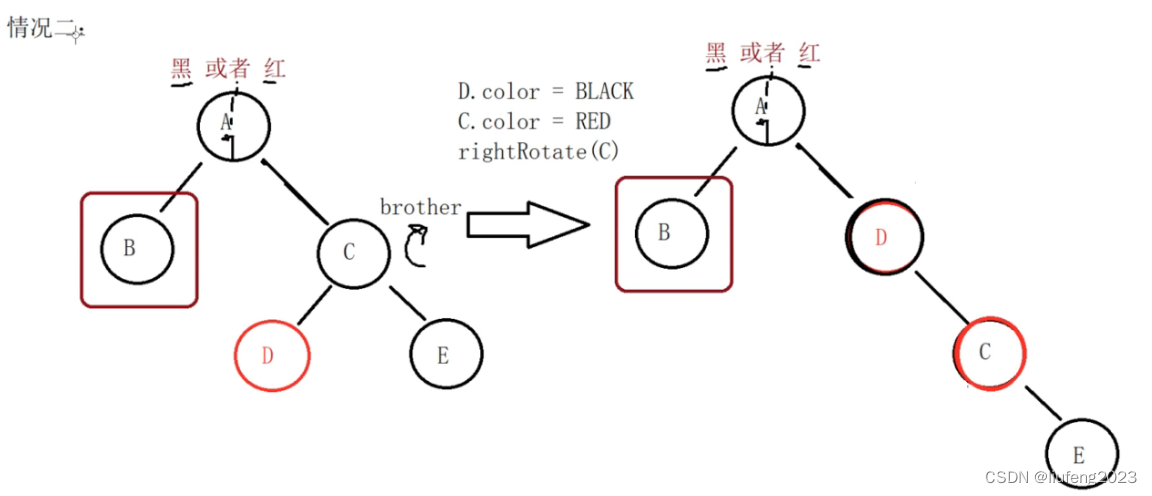
接下来就和情况1的处理一样了！！！

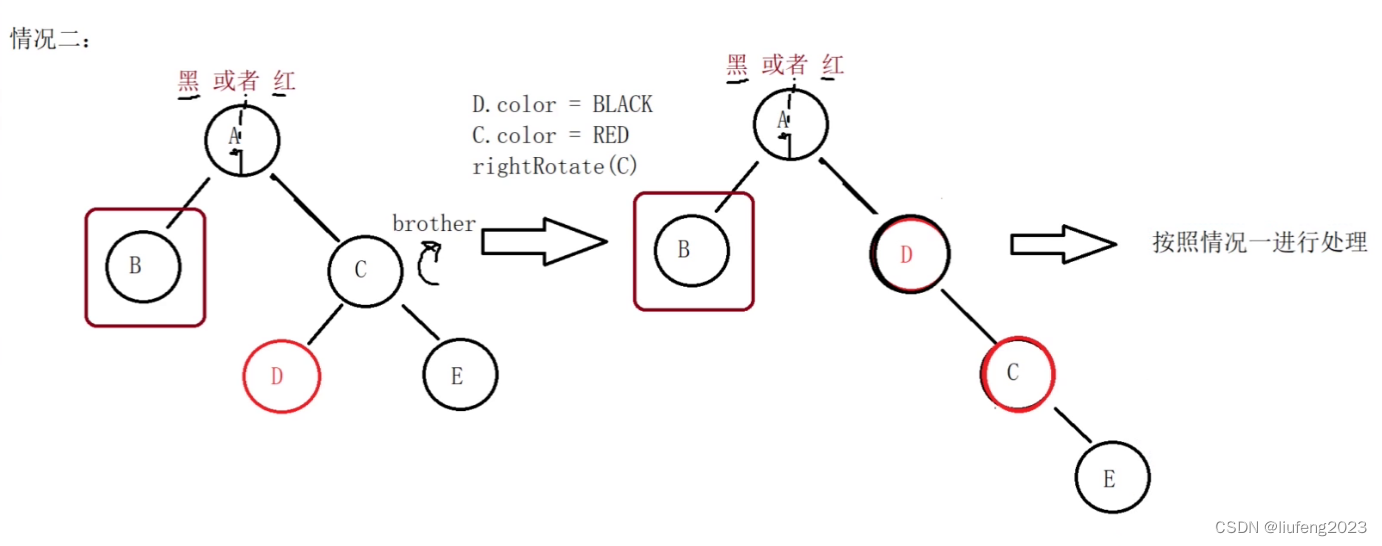
在这里插入图片描述
如果兄弟的2个节都是红色，也是归结于情况1，只需要保证兄弟的右孩子是红色，就不用关心兄弟的左孩子了

情况3：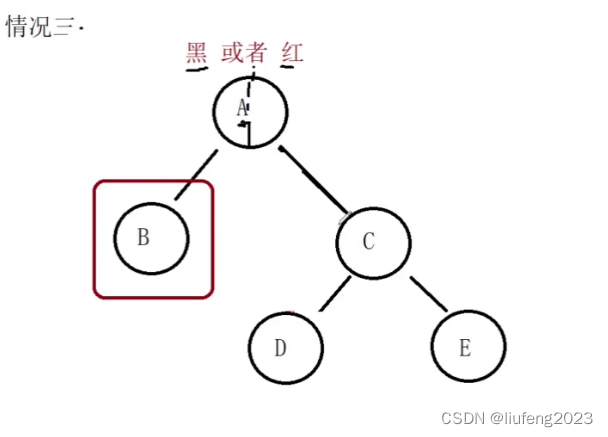
在这里插入图片描述
我们要删除B，但是B的兄弟C节点及其孩子都是黑色的。因为我们的黑色数量是不能变的。兄弟借不了你了。
如果兄弟借给你黑色，那么他就没有红色来补黑色了。

最差的情况是：只能向上一直回溯。让所有路径都少一个黑色出来。

我们来看看：

我们现在直接把兄弟涂成红色。
这样你这一路删了1个黑色，那么兄弟这一路也少了1个黑色呗。
然后node指向父节点。从父节点继续调整。
- node向上回溯，如果发现指向的是红色节点，直接把红色节点涂成黑色就OK了，这样所有路径的黑色个数就和之前的一样，而且各路径黑色个数都相等了。此时调整就结束了！！！
  
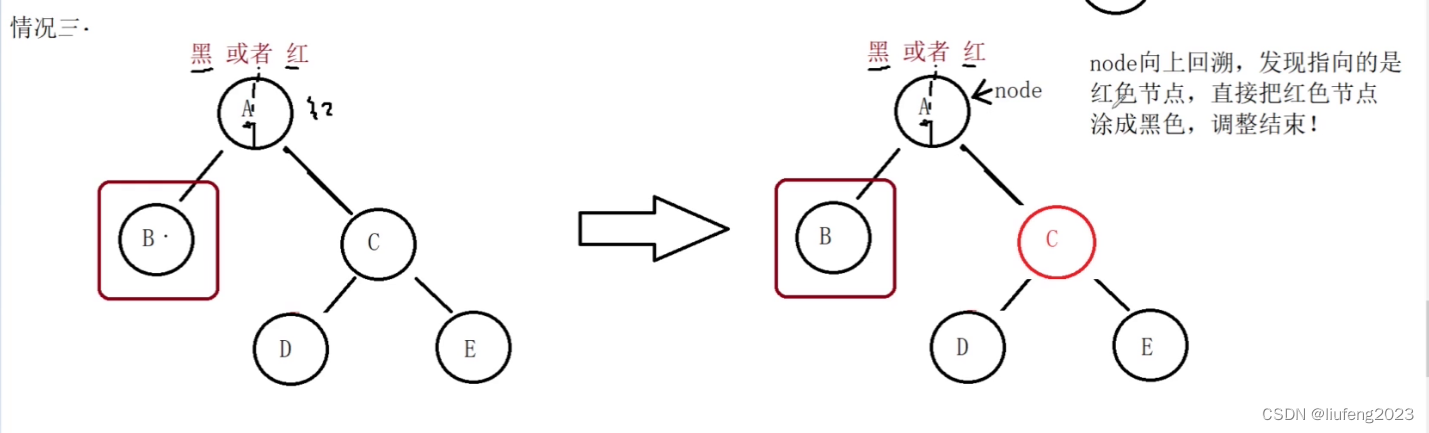
  （意思就是B的兄弟C的孩子都是黑色，左边不能向右边借，接了黑色就会不平衡了，因此：直接将兄弟C改为红色，两边都少一个，向父节点A进行借，如果A为红，直接改为黑即可；如果A为黑，即让A向他的兄弟借一下，归结在情况1, 2，4，借不到的话，将祖先的兄弟也涂为红色，继续向上回溯）
- 如果发现指向的node还是黑色节点，补不了，继续回溯上去。就继续落在四种情况之内，node是黑的，向node的兄弟借，归结在情况1, 2，4，如果借不了，就继续把node的兄弟涂成红色，然后继续回溯上去。
要么是祖先是红的涂成黑的补齐黑色个数，要么所有路径都少一个黑色。

情况4：
我们要删除B节点，但是兄弟是红色。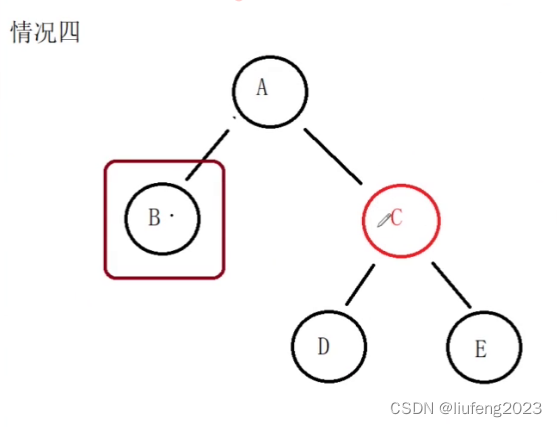
在这里插入图片描述

首先我们进行左旋转操作，C和A的颜色对调。然后以A为轴左旋转。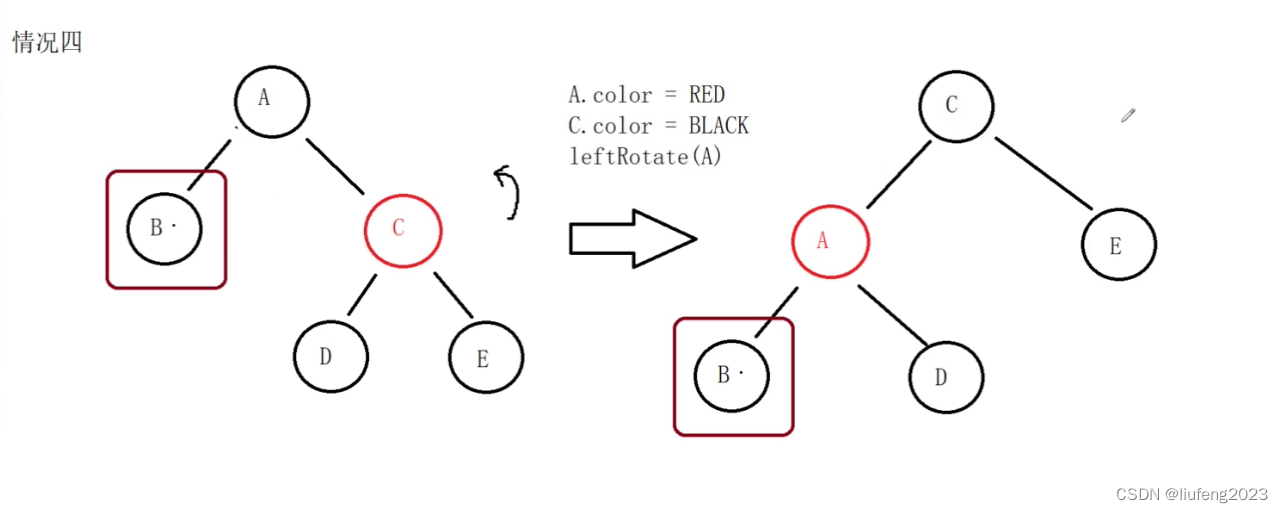
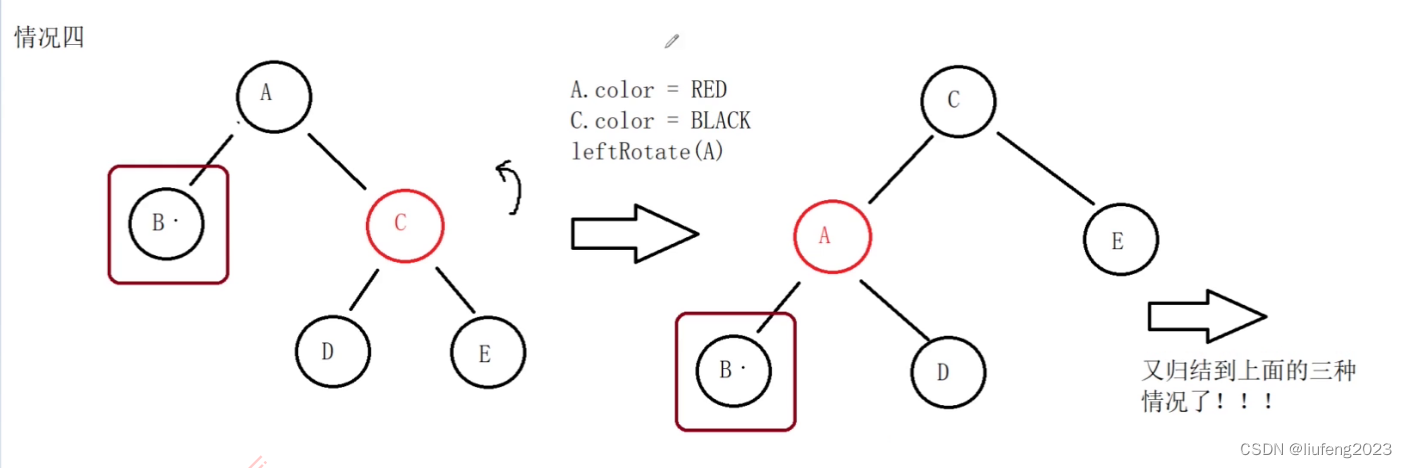
在这里插入图片描述

在这里插入图片描述
情况4处理之后，保证了现在待删除节点B的兄弟节点是黑的！

然后现在我们要删除B节点，此时又归结到上面的3种情况了：兄弟是黑色的！

10、红黑树的删除操作代码

可以看出红黑树的删除操作，最多旋转3次！（插入最多旋转2次）

//红黑树删除操作
void remove(const T& val)
{
	if (root_ == nullptr)
	{
		return;
	}

	Node* cur = root_;//指向根节点
	while (cur != nullptr)
	{
		if (cur->data_ > val)//当前节点值大于要删除的值
		{
			cur = cur->left_;
		}
		else if (cur->data_ < val)//当前节点值小于要删除的值
		{
			cur = cur->right_;
		}
		else//找到了，跳出循环
		{
			break;
		}
	}

	//如果是空，则没找到val节点，返回
	if (cur == nullptr)
	{
		return;
	}

	//删除前驱节点 情况三 有2个孩子
	if (cur->left_ != nullptr && cur->right_ != nullptr)
	{
		Node* pre = cur->left_;//定义前驱节点
		while (pre->right_ != nullptr)
		{
			pre = pre->right_;
		}
		cur->data_ = pre->data_;
		cur = pre;//cur指向前驱节点
	}

	//删除cur指向的节点  情况一和二
	Node* child = cur->left_;//让child指向不为空的孩子
	if (child == nullptr)
	{
		child = cur->right_;
	}

    //删除后，不用考虑平衡！

	//我们节点有left right parent 3个域
	if (child != nullptr)//child不为空
	{
		child->parent_ = cur->parent_;//cur是待删节点
		if (cur->parent_ == nullptr)
		{
			//root_ -> cur_
			root_ = child;
		}
		else
		{
			if (cur->parent_->left_ == cur)
			{
				cur->parent_->left_ = child;
			}
			else
			{
				cur->parent_->right_ = child;
			}
		}

		Color c = color(cur);//记录删除节点的颜色
		delete cur;

		if (c == BLACK)//删除的是黑色节点，要进行删除调整操作
		{
			fixAfterRemove(child);
		}
	}
	else//child为空
	{
		//child == nullptr
		if (cur->parent_ == nullptr)
		{
			delete cur;
			root_ = nullptr;
			return;
		}
		else
		{
			//删除的cur就是叶子节点
			if (color(cur) == BLACK)
			{
				fixAfterRemove(cur);
			}

			if (cur->parent_->left_ == cur)
			{
				cur->parent_->left_ = nullptr;
			}
			else
			{
				cur->parent_->right_ = nullptr;
			}

			delete cur;
		}
	}
}



//红黑树的删除调整操作
void fixAfterRemove(Node* node)
{
	while (node != root_ && color(node) == BLACK)
	{
		if (left(parent(node)) == node)//删除的黑色节点在左子树
		{
			Node* brother = right(parent(node));//指向兄弟
			if (color(brother) == RED)//情况四 兄弟是红色的
			{
				setColor(parent(node), RED);
				setColor(brother, BLACK);
				leftRotate(parent(node));
				brother = right(parent(node));
			}

			if (color(left(brother)) == BLACK
				&& color(right(brother)) == BLACK)//情况三 兄弟和孩子是黑的
			{
				setColor(brother, RED);
				node = parent(node);
			}
			else
			{
				if (color(right(brother)) != RED)//情况二 兄弟的右孩子不是红色的
				{
					setColor(brother, RED);
					setColor(left(brother), BLACK);
					rightRotate(brother);
					brother = right(parent(node));
				}

				//归结到情况一
				setColor(brother, color(parent(node)));
				setColor(parent(node), BLACK);
				setColor(right(brother), BLACK);
				leftRotate(parent(node));
				break;
			}
		}
		else//删除的黑色节点在右子树
		{
			Node* brother = left(parent(node));
			if (color(brother) == RED) // 情况四
			{
				setColor(parent(node), RED);
				setColor(brother, BLACK);
				rightRotate(parent(node));
				brother = left(parent(node));
			}

			if (color(left(brother)) == BLACK
				&& color(right(brother)) == BLACK)//情况三
			{
				setColor(brother, RED);
				node = parent(node);
			}
			else
			{
				if (color(left(brother)) != RED)//情况二
				{
					setColor(brother, RED);
					setColor(right(brother), BLACK);
					leftRotate(brother);
					brother = left(parent(node));
				}

				//归结到情况一
				setColor(brother, color(parent(node)));
				setColor(parent(node), BLACK);
				setColor(left(brother), BLACK);
				rightRotate(parent(node));
				break;
			}
		}
	}

	//如果发现node指向的节点是红色，直接涂成黑色，调整结束
	setColor(node, BLACK);
}

11、删除代码测试

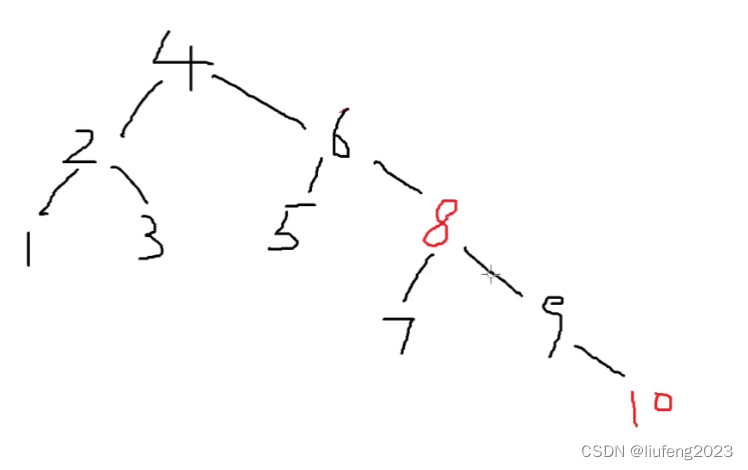
在这里插入图片描述
如果将9删除：

补上来10，10是红色，这一条路径删除了一个黑色9，这条路径的黑色节点就比其他路径的黑色节点要少了；

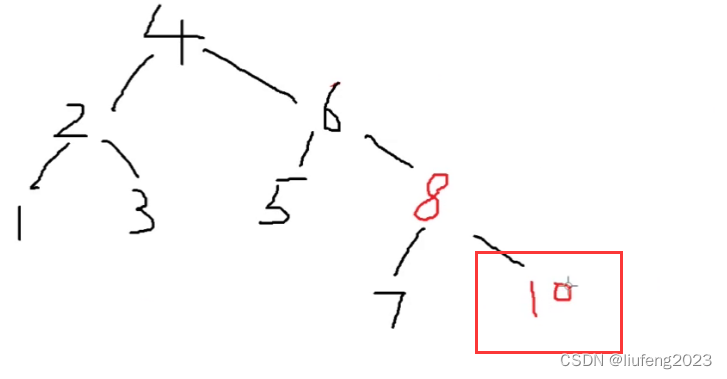
直接将10变为黑色即可，属于这种情况：

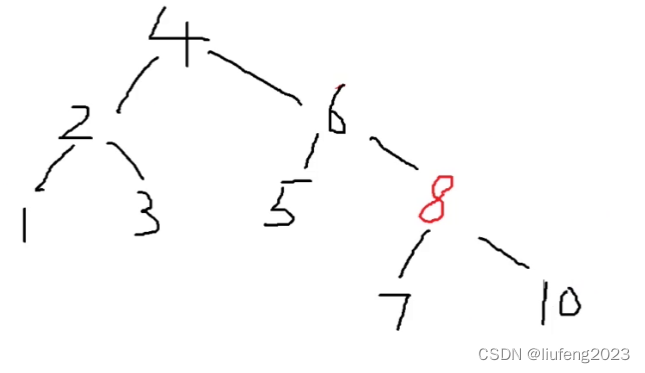
12、总体代码



template<typename T>
class RBTree
{
public:
	RBTree() :root_(nullptr) {}
	struct Node;

	//插入操作
	void insert(const T& val)
	{
		if (root_ == nullptr)
		{
			root_ = new Node(val);//刚好默认是黑色
			return;
		} 

		Node* parent = nullptr;
		Node* cur = root_;
		while (cur != nullptr)
		{
			if (cur->data_ > val)//当前节点的值大于要插入的值
			{
				parent = cur;
				cur = cur->left_;
			}
			else if (cur->data_ < val)//当前节点的值小于要插入的值
			{
				parent = cur;
				cur = cur->right_;
			}
			else//值存在，不插入重复的值
			{
				return;
			}
		}

		//设置当前节点的parent和颜色
		Node* node = new Node(val, parent, nullptr, nullptr, RED);//新节点设置成红色
		if (parent->data_ > val)
		{
			parent->left_ = node;//插在父亲的左孩子域
		}
		else
		{
			parent->right_ = node;//插在父亲的右孩子域
		}

		//如果新插入的红色节点，父节点也是红色，不满足红黑树性质，进行插入调整操作
		if (RED == color(parent))
		{
			fixAfterInsert(node);
		}
	}

	//红黑树的插入调整操作
	void fixAfterInsert(Node* node)
	{
		//如果当前红色节点的父节点也是红色，继续调整
		while (color(parent(node)) == RED)
		{
			if (left(parent(parent(node))) == parent(node))//爷爷节点的左孩子是我的父亲
			{
				//表示插入的节点在左子树当中，叔叔在右边，插入要看叔叔
				Node* uncle = right(parent(parent(node)));//叔叔在爷爷的右孩子
				if (RED == color(uncle))//情况一，叔叔节点也是红色
				{
					setColor(parent(node), BLACK);
					setColor(uncle, BLACK);
					setColor(parent(parent(node)), RED);
					node = parent(parent(node));//node指向他的爷爷，继续调整上去
				}
				else//叔叔节点是黑色
				{
					//先处理情况三，插入的节点和父亲，爷爷不在一侧
					if (right(parent(node)) == node)
					{
						node = parent(node);
						leftRotate(node);
						//进行左旋转，node此时指向的就是情况二中的左边最后一个节点的位置
					}

					//统一处理情况二
					setColor(parent(node), BLACK);
					setColor(parent(parent(node)), RED);
					rightRotate(parent(parent(node)));//右旋转，以爷爷节点进行右旋
					break;//调整已经完成
				}
			}
			else//插入的节点在右子树当中
			{
				Node* uncle = left(parent(parent(node)));
				if (RED == color(uncle))//情况一
				{
					setColor(parent(node), BLACK);
					setColor(uncle, BLACK);
					setColor(parent(parent(node)), RED);
					node = parent(parent(node));//继续调整
				}
				else
				{
					//先处理情况三
					if (left(parent(node)) == node)
					{
						node = parent(node);
						rightRotate(node);
					}

					//统一处理情况二
					setColor(parent(node), BLACK);
					setColor(parent(parent(node)), RED);
					leftRotate(parent(parent(node)));
					break;//调整已经完成
				}
			}
		}

		//此处强制root为黑色节点
		setColor(root_, BLACK);
	}

	//红黑树删除操作
	void remove(const T& val)
	{
		if (root_ == nullptr)
		{
			return;
		}

		Node* cur = root_;//指向根节点
		while (cur != nullptr)
		{
			if (cur->data_ > val)//当前节点值大于要删除的值
			{
				cur = cur->left_;
			}
			else if (cur->data_ < val)//当前节点值小于要删除的值
			{
				cur = cur->right_;
			}
			else//找到了，跳出循环
			{
				break;
			}
		}

		//如果是空，则没找到val节点，返回
		if (cur == nullptr)
		{
			return;
		}

		//删除前驱节点 情况三 有2个孩子，这里还没有删除
		if (cur->left_ != nullptr && cur->right_ != nullptr)
		{
			Node* pre = cur->left_;//定义前驱节点
			while (pre->right_ != nullptr)
			{
				pre = pre->right_;
			}
			cur->data_ = pre->data_;
			cur = pre;//cur指向前驱节点
		}

		//删除cur指向的节点  情况一和二
		Node* child = cur->left_;//让child指向不为空的孩子
		if (child == nullptr)
		{
			child = cur->right_;
		}

		//删除后，不用考虑平衡！

		//我们节点有left right parent 3个域
		if (child != nullptr)//child不为空
		{
			child->parent_ = cur->parent_;//cur是待删节点
			if (cur->parent_ == nullptr)
			{
				//root_ -> cur_
				root_ = child;
			}
			else
			{
				if (cur->parent_->left_ == cur)
				{
					cur->parent_->left_ = child;
				}
				else
				{
					cur->parent_->right_ = child;
				}
			}

			Color c = color(cur);//记录删除节点的颜色
			delete cur;

			if (c == BLACK)//删除的是黑色节点，要进行删除调整操作
			{
				fixAfterRemove(child);
			}
		}
		else//child为空
		{
			//child == nullptr
			if (cur->parent_ == nullptr)
			{
				delete cur;
				root_ = nullptr;
				return;
			}
			else
			{
				//删除的cur就是叶子节点
				if (color(cur) == BLACK)
				{
					fixAfterRemove(cur);
				}

				if (cur->parent_->left_ == cur)
				{
					cur->parent_->left_ = nullptr;
				}
				else
				{
					cur->parent_->right_ = nullptr;
				}

				delete cur;
			}
		}
	}



	//红黑树的删除调整操作
	void fixAfterRemove(Node* node)
	{
		while (node != root_ && color(node) == BLACK)
		{
			if (left(parent(node)) == node)//删除的黑色节点在左子树
			{
				Node* brother = right(parent(node));//指向兄弟
				if (color(brother) == RED)//情况四 兄弟是红色的
				{
					setColor(parent(node), RED);
					setColor(brother, BLACK);
					leftRotate(parent(node));
					brother = right(parent(node));
				}

				if (color(left(brother)) == BLACK
					&& color(right(brother)) == BLACK)//情况三 兄弟和孩子是黑的
				{
					setColor(brother, RED);
					node = parent(node);	//指针指向父亲
				}
				else
				{
					if (color(right(brother)) != RED)//情况二 兄弟的右孩子不是红色的
					{
						setColor(brother, RED);
						setColor(left(brother), BLACK);
						rightRotate(brother);
						brother = right(parent(node)); 
					}

					//最后全部归结到情况一
					setColor(brother, color(parent(node)));
					setColor(parent(node), BLACK);
					setColor(right(brother), BLACK);
					leftRotate(parent(node));
					break;
				}
			}
			else//删除的黑色节点在右子树
			{
				Node* brother = left(parent(node));
				if (color(brother) == RED) // 情况四
				{
					setColor(parent(node), RED);
					setColor(brother, BLACK);
					rightRotate(parent(node));
					brother = left(parent(node));
				}

				if (color(left(brother)) == BLACK
					&& color(right(brother)) == BLACK)//情况三
				{
					setColor(brother, RED);
					node = parent(node);
				}
				else
				{
					if (color(left(brother)) != RED)//情况二
					{
						setColor(brother, RED);
						setColor(right(brother), BLACK);
						leftRotate(brother);
						brother = left(parent(node));
					}

					//归结到情况一
					setColor(brother, color(parent(node)));
					setColor(parent(node), BLACK);
					setColor(left(brother), BLACK);
					rightRotate(parent(node));
					break;
				}
			}
		}

		//如果发现node指向的节点是红色，直接涂成黑色，调整结束
		setColor(node, BLACK);
	}


private:
	//红黑树节点的颜色
	enum Color
	{
		BLACK,
		RED
	};
	//节点类型
	struct Node
	{
		Node(T data = T(), Node* parent = nullptr,
			Node* left = nullptr, Node* right = nullptr,
			Color color = BLACK)
			:data_(data)
			, left_(left)
			, right_(right)
			, parent_(parent)
			, color_(color)
		{}
		T data_;
		Node* left_;
		Node* right_;
		Node* parent_;//指向当前节点的父节点
		Color color_; //节点的颜色
	};

	//返回节点的颜色
	Color color(Node* node)
	{
		return node == nullptr ? BLACK : node->color_;
	}
	//设置节点颜色
	void setColor(Node* node, Color color)
	{
		node->color_ = color;
	}
	//返回节点的左孩子
	Node* left(Node* node)
	{
		return node->left_;
	}
	//返回节点的右孩子
	Node* right(Node* node)
	{
		return node->right_;
	}
	//返回节点的父亲
	Node* parent(Node* node)
	{
		return node->parent_;
	}


	//左旋转
	void leftRotate(Node* node)
	{
		Node* child = node->right_;
		child->parent_ = node->parent_;
		if (node->parent_ == nullptr)
		{
			//node本身就是root节点
			root_ = child;//child变成根节点了
		}
		else//node的父节点不为空
		{
			if (node->parent_->left_ == node)//node在父节点的左孩子
			{
				node->parent_->left_ = child;
			}
			else//node在父节点的右孩子
			{
				node->parent_->right_ = child;
			}
		}

		node->right_ = child->left_;
		if (child->left_ != nullptr)
		{
			child->left_->parent_ = node;
		}

		child->left_ = node;
		node->parent_ = child;
	}

	//右旋转
	void rightRotate(Node* node)
	{
		Node* child = node->left_;
		child->parent_ = node->parent_;
		if (node->parent_ == nullptr)
		{
			//node原来就是root节点
			root_ = child;
		}
		else
		{
			if (node->parent_->left_ == node)
			{
				//node在父节点的左边
				node->parent_->left_ = child;
			}
			else
			{
				//node在父节点的右边
				node->parent_->right_ = child;
			}
		}

		node->left_ = child->right_;
		if (child->right_ != nullptr)
		{
			child->right_->parent_ = node;
		}

		child->right_ = node;
		node->parent_ = child;
	}



	//指向红黑树的根节点
	Node* root_;
};



int main()
{
	RBTree<int> rb;
	for (int i = 1; i <= 4; ++i)
	{
		rb.insert(i);
	}

	rb.remove(9);
	rb.remove(10);
	rb.remove(5);
	rb.remove(3);

	return 0;
}

原文链接：https://blog.csdn.net/Edward_LF/article/details/126170364