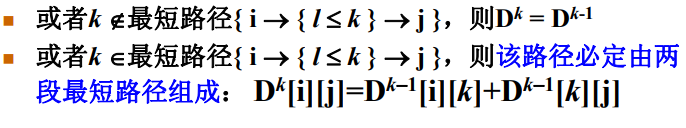本系列文章为浙江大学陈越、何钦铭数据结构学习笔记,前面的系列文章链接如下:
数据结构基础:P1-基本概念
数据结构基础:P2.1-线性结构—>线性表
数据结构基础:P2.2-线性结构—>堆栈
数据结构基础:P2.3-线性结构—>队列
数据结构基础:P2.4-线性结构—>应用实例:多项式加法运算
数据结构基础:P2.5-线性结构—>应用实例:多项式乘法与加法运算-C实现
数据结构基础:P3.1-树(一)—>树与树的表示
数据结构基础:P3.2-树(一)—>二叉树及存储结构
数据结构基础:P3.3-树(一)—>二叉树的遍历
数据结构基础:P3.4-树(一)—>小白专场:树的同构-C语言实现
数据结构基础:P4.1-树(二)—>二叉搜索树
数据结构基础:P4.2-树(二)—>二叉平衡树
数据结构基础:P4.3-树(二)—>小白专场:是否同一棵二叉搜索树-C实现
数据结构基础:P4.4-树(二)—>线性结构之习题选讲:逆转链表
数据结构基础:P5.1-树(三)—>堆
数据结构基础:P5.2-树(三)—>哈夫曼树与哈夫曼编码
数据结构基础:P5.3-树(三)—>集合及运算
数据结构基础:P5.4-树(三)—>入门专场:堆中的路径
数据结构基础:P5.5-树(三)—>入门专场:File Transfer
数据结构基础:P6.1-图(一)—>什么是图
数据结构基础:P6.2-图(一)—>图的遍历
数据结构基础:P6.3-图(一)—>应用实例:拯救007
数据结构基础:P6.4-图(一)—>应用实例:六度空间
数据结构基础:P6.5-图(一)—>小白专场:如何建立图-C语言实现
数据结构基础:P7.1-图(二)—>树之习题选讲:Tree Traversals Again
数据结构基础:P7.2-图(二)—>树之习题选讲:Complete Binary Search Tree
数据结构基础:P7.3-图(二)—>树之习题选讲:Huffman Codes
文章目录
一、概述
前面我们讲到007从一个孤岛上给你发了一个求救信号,当时我们只能回给他一个yes或者是no。如果他真的可以活命的话,你不仅仅是要告诉他一个yes,你应该告诉他怎么样跳才能跳到岸上去。当然你给他的这个路径不能让他很欢乐地在整个池塘里头把所有的鳄鱼踩一遍,你需要告诉他的是他能够跳上岸的最少的步骤。
最短路径问题:
在网络中,求两个不同顶点之间的所有路径中,边的权值之和最小的那一条路径
①这条路径就是两点之间的最短路径(Shortest Path)
②第一个顶点为源点(Source)
③最后一个顶点为终点(Destination)
问题分类:
单源最短路径问题:从某固定源点出发,求其到所有其他顶点的最短路径
------(有向)无权图
------(有向)有权图
多源最短路径问题:求任意两顶点间的最短路径
二、无权图的单源最短路
无权图的单源最短路算法:按照递增(非递减)的顺序找出到各个顶点的最短路
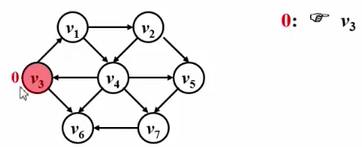
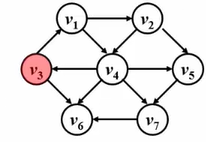
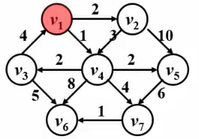
例子:我们有一张图,源点是 v 3 v_3v3 ,去找它到其它顶点的最短路。
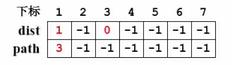
①这个问题的初始情况就是从一个路径长度为0的路径开始,也就是说源点到它自己是不用走路的,所以它的路径长度是0,我们给它标记一下。
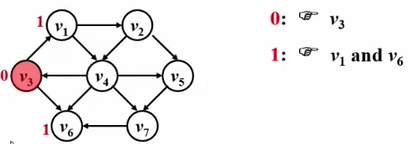
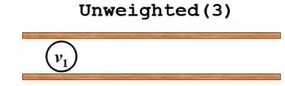
②到源点的距离是1的有 v 1 v_1v1 和 v 6 v_6v6 ,这两个顶点我把它标记一下,它们的路径长度分别为1。
③从 v 1 v_1v1 和 v 6 v_6v6 出发,找下一个结点。v 6 v_6v6 没有,v 1 v_1v1 有 v 2 v_2v2 和 v 4 v_4v4两个点可以去。
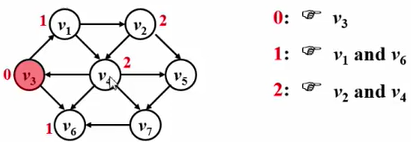
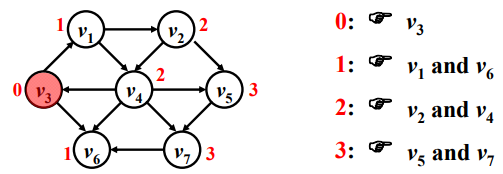
④从 v 2 v_2v2 和 v 4 v_4v4 出发,找下一个结点。v 2 v_2v2 有 v 4 v_4v4 和 v 5 v_5v5,但是 v 4 v_4v4 访问过,故不考虑。v 4 v_4v4 有 v 5 v_5v5 和 v 7 v_7v7。
⑤到此为止我们发现所有的顶点都已经被访问过了,我们这个算法就结束了。
回顾这个算法流程,我们发现这些顶点是一个一个被收罗进来的。收罗的顺序是从 v 3 v_3v3 的直接邻接点开始,然后一圈一圈往外扩展的。这让我们想到一个老朋友------广度优先搜索(BFS)。我们先来回顾一下上周我们讲过的这个 BFS。
/*
bfs 要执行的话需要先有一个初始点,从这个初始点出发,
我说我已经访问过他了,然后把他压到那个队列里。
然后就进入这个队列的循环,每次从队列里弹出一个结点,
然后去看一下他的每个邻接点。如果还没有被访问过我就访问他一下,
然后再把它压到队列里面。
*/
void BFS ( Vertex S )
{
visited[S] = true;
Enqueue(S, Q);
while(!IsEmpty(Q)){
V = Dequeue(Q);
for ( V 的每个邻接点 W )
if ( !visited[W] ) {
visited[W] = true;
Enqueue(W, Q);
}
}
}
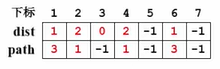
在我们的最短路的算法里头,visited这个东西是不需要的,所以删除掉。但是与此同时,我们仍然需要另外的东西来让我们能够判断这个顶点有没有被访问过。我们定义了另外一个数组,叫做dist。dist[W] = 源点S到W的最短距离,dist[S] = 0。dist[w]除了记录s到w的最短距离以外,他还相当于一个 visited。他还没有被访问过的时候,我只要把他随便定义成一个你一看就知道是不可能的数字,如-1。我们还定义一个数组path,path[W] = S到W的路上经过的某顶点,这里一般定义为S到W的倒数第二个顶点,即W前面一个结点。对应伪代码如下:
void Unweighted ( Vertex S )
{
Enqueue(S, Q);
while(!IsEmpty(Q)){
V = Dequeue(Q);
for ( V 的每个邻接点 W )
if ( dist[W]==-1 ) {
dist[W] = dist[V]+1; //记录最短路径
path[W] = V; //从S到W的路径,V代表倒数第二个结点
/*
path[W] = V, path[V] = U.....path[T]=S
这样一直往回数就能得到路径了,但是是反向的。
可以勇哥堆栈,数一个就压进去一个,最后又弹出来。
*/
Enqueue(W, Q);
}
}
}
在这个算法中,每一个结点访问了两次,每一条边访问了一次,算法总体复杂度为:T = O ( ∣ V ∣ + ∣ E ∣ ) {\rm{T = O(|V| + |E|)}}T=O(∣V∣+∣E∣)
三、无权图的单源最短路示例
我们仍然以前面那张图为例子: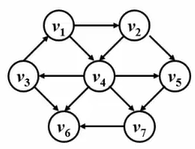
现在要找出源点到各结点的最短路,步骤如下:
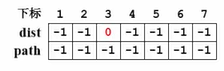
源点为 v 3 v_3v3,将其标记
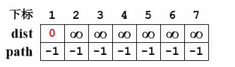
对两个数组进行初始化
开始调用Unweighted函数,将源点的下标3传入,并将源点 v 3 v_3v3 入队。
进入while循环,检查队列是否为空。此时不为空,出队一个元素 v 3 v_3v3 。
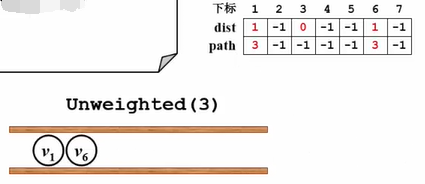
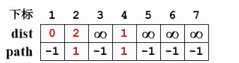
对 v 3 v_3v3 的邻接点 v 1 v_1v1 和 v 6 v_6v6 进行检查。首先检查 v 1 v_1v1,dist[1]=-1,所以未访问,开始更新dist[1]=dist[3]+1=1和path[1]=3代表结点1的上一个结点是3;
将 v 1 v_1v1 压入队列。
接着检查 v 6 v_6v6 ,未访问,更新两个数组,并将 v 6 v_6v6 入队。
我们对 v 3 v_3v3 完成了所有的操作,离开这个for循环,回到while。此时队列不为空,出队一个元素 v 1 v_1v1,继续执行上面的步骤。
更新 v 1 v_1v1 的两个邻接点 v 2 v_2v2 和 v 4 v_4v4 对应的数组数据
并将v 2 v_2v2 和 v 4 v_4v4入队。
v 1 v_1v1 处理完了,回到while。此时队列不为空,出队一个元素 v 6 v_6v6。v 6 v_6v6 没有邻接点,所以不会执行for循环,继续回到while。
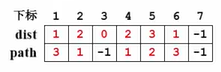
此时队列不为空,出队一个元素 v 2 v_2v2。
更新 v 2 v_2v2 的邻接点 v 5 v_5v5 对应的数组数据(v 4 v_4v4 不用更新,因为已经访问过)
v 5 v_5v5 进队
回到while循环,此时队列不空,出队一个元素 v 4 v_4v4。
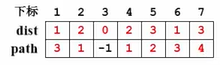
v 4 v_4v4有4个邻接点(v 3 v_3v3,v 5 v_5v5,v 6 v_6v6,v 7 v_7v7),只有 v 7 v_7v7 未访问。更新 v 7 v_7v7 对应的数组数据。
v 7 v_7v7 处理完了,入队。
回到while循环,由于 v 5 v_5v5 和 v 7 v_7v7都访问过,所以直接出队。此时队列空了,整个算法结束。
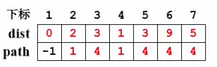
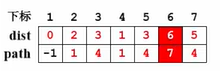
假如要输入 v 3 v_3v3 到 v 7 v_7v7 的最短距离,这个信息就存储在path这个数组里面。我们从path[7]=4出发,意味着 v 4 v_4v4 是到达 v 7 v_7v7 的前一个顶点。接着去检查path[4]=1,意味着v 1 v_1v1 是到达 v 4 v_4v4 的前一个顶点。接着去检查path[1]=3,意味着 v 3 v_3v3 是到达 v 1 v_1v1 的前一个顶点。接着去检查path[3]=-1,也就意味着 v 3 v_3v3 就是源点。我们找到了源点,那反过来说从 v3 _33 到 v 7 v_7v7 的最短路径就是从 v 3 v_3v3 到 v 1 v_1v1 到 v 4 v_4v4 再到 v 7 v_7v7
四、有权图的单源最短路
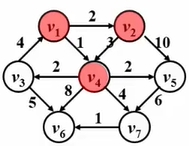
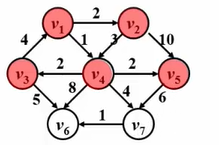
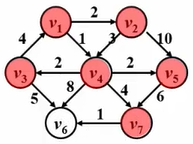
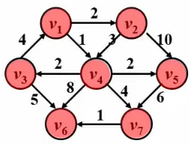
我们来看一个例子,假如说我们把 v 1 v_1v1 选做我们的源点,把 v 6 v_6v6 选做我们的终点,那么从 v 1 v_1v1 到 v 6 v_6v6 最短的路径是哪一条呢?可以看到有权图的最短路不一定是经过顶点数最少的那条路,它是权重最小的一条路。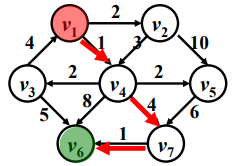
如果某一条边的权重是负的会发生什么情况呢?如果我把 v 5 v_5v5 作为源点,然后把 v 4 v_4v4 作为终点的话,有趣的事情发生了。我实际上可以沿着这条回路走无穷多次,我只要在这不停的兜圈子,我的收入会是无穷大。这种情况叫做有一个负值圈(negative-cost cycle),如果我们图里头有这样一个负值圈,我们基本上所有的算法都挂掉了,所以我们在后头讨论的时候不考虑这种情况。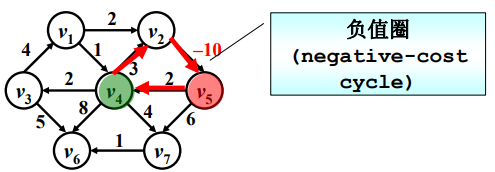
整个问题的思路跟无权图的单源最短路还是有一定相似之处的,无权图其实是一个种特殊的有权图,只不过每条边上的权重唯一。所以他们的算法肯定有相通之处,最重要的一个特点都是按照递增的顺序(非递减的顺序)找出这个固定的源点到各个顶点的最短路。解决这个问题的算法有一个金光闪闪的名字,叫Dijkstra算法。
Dijkstra算法
Dijkstra算法其实跟那个我们前面讲的 BFS相似的地方在于:都是把顶点一个一个往他的那个集合里面收。
①所以我们先定义一个顶点的集合s,初始状态下它只包含这个源点,然后随着这个算法一步一步的进行,我们把一个一个的顶点不断的往里收。收进来的顶点他们的最短路径都是已经最后确认了的。
令S={源点S + 已经确定了最短路径的顶点 v i v_ivi}
②对任一未收录的顶点v,定义dist[v]为s到v的最短路径长度,但该路径仅经过S中的顶点,即路径{ s → ( v i ∈ S ) → v } {\rm{\{ s}} \to {\rm{(}}{{\rm{v}}_{\rm{i}}} \in {\rm{S)}} \to {\rm{v\} }}{s→(vi∈S)→v}的最小长度。这个最小长度多半不是最终的那个最小长度,但是随着一个一个顶点不断的被加到这个集合里,dist[v]会慢慢的变小,一直最后被完善到成为真正的那个最短路径。当他成为真正最短路径的时候,这个v就被收到了这个集合里面。
③这个算法能够这样执行的一个很重要的前提假设是:我们的路径是按照递增或者非递减的顺序生成的。若路径是按照递增(非递减)的顺序生成的,则
------当我们要把下一个v收到顶点里去的时候,那么这个v真正的最短路必须只经过S中的顶点。反证法:如果s到v要经过S外的一个顶点w,而v是即将收入S的,那么s到w的距离一定小于s到v的距离,说明w应该在S内,矛盾。
------每次从未收录的顶点中选一个dist最小的收录(贪心算法)
------增加一个v进入S,可能影响另外一个w的dist值!此时s到w的路径一定经过v,并且v到w有一条直接的边。再说的清楚一点,v 增加进这个集合以后,他能影响的就是他的一圈邻接点。所以在程序里面我们只要每把一个v收进集合的时候,我们只要检查他的一圈邻接点,看看有没有谁能够得到一个更小的dist[w]。
dist[w] = min{dist[w], dist[v] + <v,w>的权重}
算法对应的伪代码如下:
void Dijkstra( Vertex s )
{
while (1) {
V = 未收录顶点中dist最小者;
if ( 这样的V不存在 )
break;
collected[V] = true;
for ( V 的每个邻接点 W )
if ( collected[W] == false )
if ( dist[V]+E<V,W> < dist[W] ) {
dist[W] = dist[V] + E<V,W> ;
path[W] = V;
}
}
} /* 不能解决有负边的情况 */
算法的时间复杂度取决于如何去解决V = 未收录顶点中dist最小者和dist[W] = dist[V] + E<V,W>这两个问题:
方法1:直接扫描所有未收录顶点----O ( ∣ V ∣ ) O(|V|)O(∣V∣)
T = O ( ∣ V ∣ 2 + ∣ E ∣ ) {\rm{T = O(}}{\left| {\rm{V}} \right|^{\rm{2}}}{\rm{ + }}\left| {\rm{E}} \right|{\rm{)}}T=O(∣V∣2+∣E∣),对于稠密图效果好
方法2:将dist存在最小堆中----O ( l o g ∣ V ∣ ) O\rm{(log|V|)}O(log∣V∣)
更新dist[w]的值----O ( l o g ∣ V ∣ ) O\rm{(log|V|)}O(log∣V∣)
T = O ( ∣ V ∣ l o g ∣ V ∣ + ∣ E ∣ l o g ∣ V ∣ ) = O ( ∣ E ∣ l o g ∣ V ∣ ) T = \rm{O(|V|log|V|+|E|log|V|) = O(|E|log|V|)}T=O(∣V∣log∣V∣+∣E∣log∣V∣)=O(∣E∣log∣V∣),对于稀疏图效果好
五、有权图的单源最短路示例
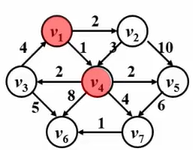
例子:我们有以下这张有权图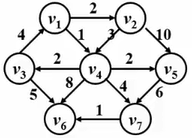
现在求源点到各个顶点地最短路,步骤如下:
首先,我们设定 v 1 v_1v1 为源点
同时初始化两个数组
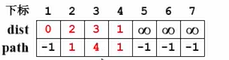
遍历 v 1 v_1v1 的两个邻接点 v 2 v_2v2 和 v 4 v_4v4,更新对应的数组。
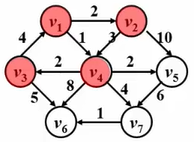
正式进入Dijkstra算法,传入源点,进入while循环。首先,我们要从未收录的顶点中选一个距离最小的出来。不管是直接扫描还是用最小堆,总之我们找了一下,这里面 v 1 v_1v1 不算,因为他本身是源点。除此之外下一个点就是 v 4 v_4v4 了,这个距离最小,所以现在这个V是等于 v 4 v_4v4 的。找个这个定点后,collect[4]=true,标记为访问过。
接着对 v 4 v_4v4 的每个邻接点w(v 3 v_3v3,v 5 v_5v5,v 6 v_6v6,v 7 v_7v7) 做下面的事:
首先是v 3 v_3v3:
①collected[3]=false,所以继续往下执行。
②由于d i s t [ 4 ] ( 1 ) + E ⟨ 4 , 3 ⟩ ( 2 ) < d i s t [ 3 ] ( ∞ ) {\rm{dist[4](1) + }}{{\rm{E}}_{\left\langle {{\rm{4,3}}} \right\rangle }}{\rm{(2) < dist[3](}}\infty {\rm{)}}dist[4](1)+E⟨4,3⟩(2)<dist[3](∞)
③d i s t [ 3 ] = d i s t [ 4 ] + E ⟨ 4 , 3 ⟩ = 1 + 2 = 3 {\rm{dist[3] = dist[4] + }}{{\rm{E}}_{\left\langle {{\rm{4,3}}} \right\rangle }} = 1 + 2 = 3dist[3]=dist[4]+E⟨4,3⟩=1+2=3
④p a t h [ 3 ] = 4 {\rm{path[3] = 4}}path[3]=4
⑤更新数组
接着是 v 5 v_5v5 ,collected[5]=false,对v 5 v_5v5执行上面相同的操作。
接着是 v 6 v_6v6 ,collected[6]=false,对v 6 v_6v6执行上面相同的操作。
接着是 v 7 v_7v7 ,collected[7]=false,对v 7 v_7v7执行上面相同的操作。
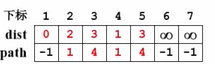
到此,v 4 v_4v4 对应的for循环处理完了。那我们进入下一轮循环,继续从没有收录的顶点中去找那个dist。最小的那个顶点显然是顶点2,那我们把顶点2标记为已访问。
然后对顶点 v 2 v_2v2 的每个邻接点w,即 v 4 v_4v4 和 v 5 v_5v5来做下面的操作。因为 v 4 v_4v4 已经被访问过了,collected[4]=true,所以我们跳过不管,直接看 v 5 v_5v5。collected[5]=false,对v 5 v_5v5执行上面相同的操作:d i s t [ 2 ] ( 2 ) + E ⟨ 2 , 5 ⟩ ( 10 ) > d i s t [ 5 ] ( 3 ) {\rm{dist[2](2) + }}{{\rm{E}}_{\left\langle {{\rm{2,5}}} \right\rangle }}{\rm{(10) > dist[5](}}3 {\rm{)}}dist[2](2)+E⟨2,5⟩(10)>dist[5](3),显然他比原来的这个距离要大很多,也就是说这个距离实际上大于当前的最短距离。在这种情况下我们就保持 v 5 v_5v5 原来的路径不变,直接进入下一轮的循环。
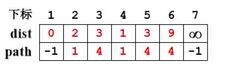
关于 v 2 v_2v2 的处理结束了,去V里面找下一个dist最小的v。我们这有两个候选人 v 3 v_3v3 和 v 5 v_5v5。那我们随便挑一个,从编号小的 v 3 v_3v3 开始。将其设置为已访问。
v 3 v_3v3 的邻接点 v 1 v_1v1 已经被访问,现在去处理 v 6 v_6v6。
①d i s t [ 3 ] ( 3 ) + E ⟨ 3 , 6 ⟩ ( 5 ) < d i s t [ 6 ] ( 9 ) {\rm{dist[3](3) + }}{{\rm{E}}_{\left\langle {{\rm{3,6}}} \right\rangle }}{\rm{(5) < dist[6](}}9 {\rm{)}}dist[3](3)+E⟨3,6⟩(5)<dist[6](9)
②d i s t [ 6 ] = d i s t [ 3 ] + E ⟨ 3 , 6 ⟩ = 3 + 5 = 8 {\rm{dist[6] = dist[3] + }}{{\rm{E}}_{\left\langle {{\rm{3,6}}} \right\rangle }} = 3 + 5 = 8dist[6]=dist[3]+E⟨3,6⟩=3+5=8
③p a t h [ 6 ] = 3 {\rm{path[6] = 3}}path[6]=3
更新对应数组
关于 v 3 v_3v3 的处理结束了,去V里面找下一个dist最小的v,得到 v 5 v_5v5。
v 5 v_5v5 的邻接点只有 v 7 v_7v7,于是去处理 v 7 v_7v7。
①d i s t [ 5 ] ( 3 ) + E ⟨ 5 , 7 ⟩ ( 6 ) > d i s t [ 7 ] ( 5 ) {\rm{dist[5](3) + }}{{\rm{E}}_{\left\langle {{\rm{5,7}}} \right\rangle }}{\rm{(6) > dist[7](}}5 {\rm{)}}dist[5](3)+E⟨5,7⟩(6)>dist[7](5),所以不更新。
关于 v 5 v_5v5 的处理结束了,去V里面找下一个dist最小的v,得到 v 7 v_7v7,设置为已放问。
v 7 v_7v7 的邻接点只有 v 6 v_6v6,于是去处理v 6 v_6v6。
①d i s t [ 7 ] ( 5 ) + E ⟨ 7 , 6 ⟩ ( 1 ) < d i s t [ 7 ] ( 8 ) {\rm{dist[7](5) + }}{{\rm{E}}_{\left\langle {{\rm{7,6}}} \right\rangle }}{\rm{(1) < dist[7](}}8 {\rm{)}}dist[7](5)+E⟨7,6⟩(1)<dist[7](8)
②d i s t [ 6 ] = d i s t [ 7 ] + E ⟨ 7 , 6 ⟩ = 5 + 1 = 6 {\rm{dist[6] = dist[7] + }}{{\rm{E}}_{\left\langle {{\rm{7,6}}} \right\rangle }} = 5 + 1 = 6dist[6]=dist[7]+E⟨7,6⟩=5+1=6
③p a t h [ 6 ] = 7 {\rm{path[6] = 7}}path[6]=7
更新对应数组
最后只剩个 v 6 v_6v6,标记为已访问
因为 v 6 v_6v6 并没有任何的邻接点,所以这个循环很快就结束了。那到现在为止我们再去找没有收入顶点中, dist最小的是谁。我们会发现这样的顶点已经不存在了。这样我们就从这个 while 循环里面跳出来结束了这个算法。
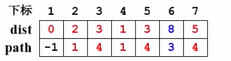
-----假设现在要求从原点 v 1 v_1v1 到终点 v 6 v_6v6 的最短路径是哪一条。我们从path[6]开始找到7,知道 v 7 v_7v7 是他的前一个顶点。然后从path[7] 开始找到4,知道 v 4 v_4v4 是他的前一个节点。再从path[4]找到 1,我们知道 v 6 v_6v6是 它的前一个顶点。检查 path[1]的时候我们得到-1,我们知道 v 1 v_1v1 就是源点,于是我们得到了这条路径:1------4------7------6。
六、多源最短路算法
之前我们说过,可以把单元最短路的算法对每一个顶点实施一次,就能得到多源最短路算法。
方法1:直接将单源最短路算法调用|V|遍
T = O ( ∣ V ∣ 3 + ∣ E ∣ × ∣ V ∣ ) {\rm{T = O(}}{\left| {\rm{V}} \right|^{\rm{3}}}{\rm{ + |E| \times }}\left| {\rm{V}} \right|{\rm{)}}T=O(∣V∣3+∣E∣×∣V∣)------>对于稀疏图效果好
方法2:Floyd算法
T = O ( ∣ V ∣ 3 ) {\rm{T = O(}}{\left| {\rm{V}} \right|^{\rm{3}}}{\rm{)}}T=O(∣V∣3)------>对于稠密图效果好
Floyd 算法
D k [ i ] [ j ] = 路 径 { i → { l ≤ k } → j } 的 最 小 长 度 {{\rm{D}}^k}[i][j] = 路径\{ i \to \{ l \le k\} \to j\}的最小长度Dk[i][j]=路径{i→{l≤k}→j}的最小长度
D 0 , D 0 , . . . , D ∣ V ∣ − 1 [ i ] [ j ] {{\rm{D}}^{\rm{0}}}{\rm{,}}{{\rm{D}}^{\rm{0}}}{\rm{,}}...{\rm{,}}{{\rm{D}}^{{\rm{|V| - 1}}}}{\rm{[i][j]}}D0,D0,...,D∣V∣−1[i][j]即给出了i到j的真正最短距离
最初的D − 1 D^{-1}D−1是什么?
当D k − 1 D^{k-1}Dk−1已经完成,递推到D k D^{k}Dk时:
对应代码如下:
void Floyd()
{
for ( i = 0; i < N; i++ )
for( j = 0; j < N; j++ ) {
D[i][j] = G[i][j];
path[i][j] = -1;
}
for( k = 0; k < N; k++ )
for( i = 0; i < N; i++ )
for( j = 0; j < N; j++ )
if( D[i][k] + D[k][j] < D[i][j] ) {
D[i][j] = D[i][k] + D[k][j];
path[i][j] = k;
}
}
邻接表存储:无权图的单源最短路算法
/* 邻接表存储 - 无权图的单源最短路算法 */
/* dist[]和path[]全部初始化为-1 */
void Unweighted ( LGraph Graph, int dist[], int path[], Vertex S )
{
Queue Q;
Vertex V;
PtrToAdjVNode W;
Q = CreateQueue( Graph->Nv ); /* 创建空队列, MaxSize为外部定义的常数 */
dist[S] = 0; /* 初始化源点 */
AddQ (Q, S);
while( !IsEmpty(Q) ){
V = DeleteQ(Q);
for ( W=Graph->G[V].FirstEdge; W; W=W->Next ) /* 对V的每个邻接点W->AdjV */
if ( dist[W->AdjV]==-1 ) { /* 若W->AdjV未被访问过 */
dist[W->AdjV] = dist[V]+1; /* W->AdjV到S的距离更新 */
path[W->AdjV] = V; /* 将V记录在S到W->AdjV的路径上 */
AddQ(Q, W->AdjV);
}
} /* while结束*/
}
邻接矩阵存储:有权图的单源最短路算法
/* 邻接矩阵存储 - 有权图的单源最短路算法 */
Vertex FindMinDist( MGraph Graph, int dist[], int collected[] )
{ /* 返回未被收录顶点中dist最小者 */
Vertex MinV, V;
int MinDist = INFINITY;
for (V=0; V<Graph->Nv; V++) {
if ( collected[V]==false && dist[V]<MinDist) {
/* 若V未被收录,且dist[V]更小 */
MinDist = dist[V]; /* 更新最小距离 */
MinV = V; /* 更新对应顶点 */
}
}
if (MinDist < INFINITY) /* 若找到最小dist */
return MinV; /* 返回对应的顶点下标 */
else return ERROR; /* 若这样的顶点不存在,返回错误标记 */
}
bool Dijkstra( MGraph Graph, int dist[], int path[], Vertex S )
{
int collected[MaxVertexNum];
Vertex V, W;
/* 初始化:此处默认邻接矩阵中不存在的边用INFINITY表示 */
for ( V=0; V<Graph->Nv; V++ ) {
dist[V] = Graph->G[S][V];
if ( dist[V]<INFINITY )
path[V] = S;
else
path[V] = -1;
collected[V] = false;
}
/* 先将起点收入集合 */
dist[S] = 0;
collected[S] = true;
while (1) {
/* V = 未被收录顶点中dist最小者 */
V = FindMinDist( Graph, dist, collected );
if ( V==ERROR ) /* 若这样的V不存在 */
break; /* 算法结束 */
collected[V] = true; /* 收录V */
for( W=0; W<Graph->Nv; W++ ) /* 对图中的每个顶点W */
/* 若W是V的邻接点并且未被收录 */
if ( collected[W]==false && Graph->G[V][W]<INFINITY ) {
if ( Graph->G[V][W]<0 ) /* 若有负边 */
return false; /* 不能正确解决,返回错误标记 */
/* 若收录V使得dist[W]变小 */
if ( dist[V]+Graph->G[V][W] < dist[W] ) {
dist[W] = dist[V]+Graph->G[V][W]; /* 更新dist[W] */
path[W] = V; /* 更新S到W的路径 */
}
}
} /* while结束*/
return true; /* 算法执行完毕,返回正确标记 */
}
邻接矩阵存储:多源最短路算法
/* 邻接矩阵存储 - 多源最短路算法 */
bool Floyd( MGraph Graph, WeightType D[][MaxVertexNum], Vertex path[][MaxVertexNum] )
{
Vertex i, j, k;
/* 初始化 */
for ( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ ) {
D[i][j] = Graph->G[i][j];
path[i][j] = -1;
}
for( k=0; k<Graph->Nv; k++ )
for( i=0; i<Graph->Nv; i++ )
for( j=0; j<Graph->Nv; j++ )
if( D[i][k] + D[k][j] < D[i][j] ) {
D[i][j] = D[i][k] + D[k][j];
if ( i==j && D[i][j]<0 ) /* 若发现负值圈 */
return false; /* 不能正确解决,返回错误标记 */
path[i][j] = k;
}
return true; /* 算法执行完毕,返回正确标记 */
}