马尔萨斯与阻滞增长模型对于人口预测的分析

一、问题重述

  1790-1980年间美国人口记录表：

用以上数据建立马尔萨斯(Malthus)人口指数增长模型。

二、问题假设

1.假设所给的数据真实可靠;

2.各个年龄段的性别比例大致保持不变;

3.人口变化不受外界大的因素的影响；

4.马尔萨斯人口模型

（1）单位时间的人口增长率r为常数；

（2）将x（t）视为t的连续可微函数。

5.改进后的模型（阻滞增长模型）

(1)人口净增长率r为变化量。

三、变量说明

X(t)  t时刻的人口数量

X1790  1790年的的人口数量

r  人口净增长率

Xm  环境所能容纳的最大人口数量，即

四、模型建立

指数增长模型---马尔萨斯模型

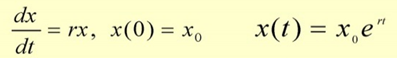
阻滞增长模型（Logistic模型）

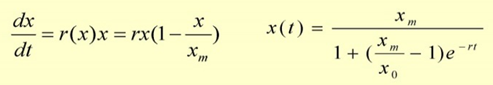
五、模型求解

输入数据

t=[1790:10:1980];

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5];

1.马尔萨斯模型求解

在matlab里用应用程序中的Curve Fitting求参数，得：

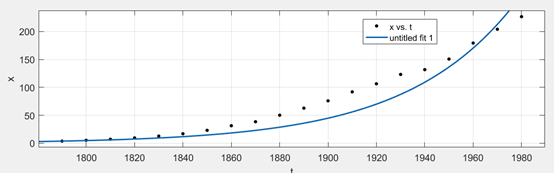
图1.马尔萨斯人口模型

参数：

Coefficients (with 95% confidence bounds):

       r =     0.02222  (0.02163, 0.02281)

预测：

每个十年，从1990—2030：

y1 =

  331.9474  414.5429  517.6900  646.5022  807.3656

查阅相关年份美国实际人口数据，1990年为248.7百万，2000年为281.4百万，2010年为307.0百万。可以看出马尔萨斯模型预测人口与实际相差很大，而且到后来增长速度变快，主要原因是没有抑制因素。

2.阻滞增长模型求解

在matlab里用应用程序中的Curve Fitting求参数，得：

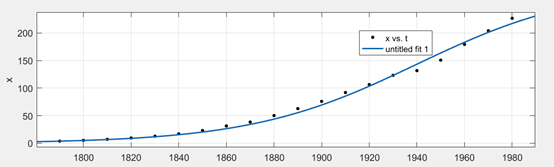
图2阻滞增长模型与实际人口数据

参数：

   a =       285.9  (257.4, 314.4)

   r =     0.02858  (0.02763, 0.02953)

预测：

每个十年，从1990—2030：

y2 =

  230.9171  242.5109  252.0186  259.6683  265.7291

改进后的模型与实际人口数据很接近。但依然有一定的误差。

3.观察两种模型及原数据的图像。

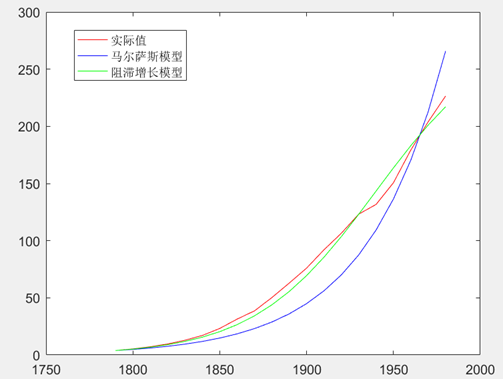
图3.两个模型与实际人口数据的对比

由图可以看出，阻滞增长模型相比于马尔萨斯模型与实际曲线拟合效果更好。

六、结果分析

1.马尔萨斯模型为指数增长模型，符合人口增长特点，但忽视了资源有限等外部条件，在最初效果可以，预测时间越长，与实际偏离程度越大。

2. 阻滞增长模型在指数增长的基础上添加了修正因子，使得模型包含自我抑制作用，考虑到了外部资源、环境容纳量等现实因素，对于人口预测有比指数模型更好的意义。

七．实验代码

t=[1790:10:1980];

x=[3.9 5.3 7.2 9.6 12.9 17.1 23.2 31.4 38.6 50.2 62.9 76.0 92.0 106.5 123.2 131.7 150.7 179.3 204.0 226.5];

y1=3.9*exp(0.02222.*(t-1790));

y2=285.9./(1+72.31*exp(-0.02858.*(t-1790)));

plot(t,x,'r',t,y1,'b',t,y2,'g');

legend('实际值','马尔萨斯模型','阻滞增长模型')