做题记录2021.8.29 牛客IOI周赛28

昨天晚上参加牛客IOI周赛普及组，以下是个人做题记录：

1.


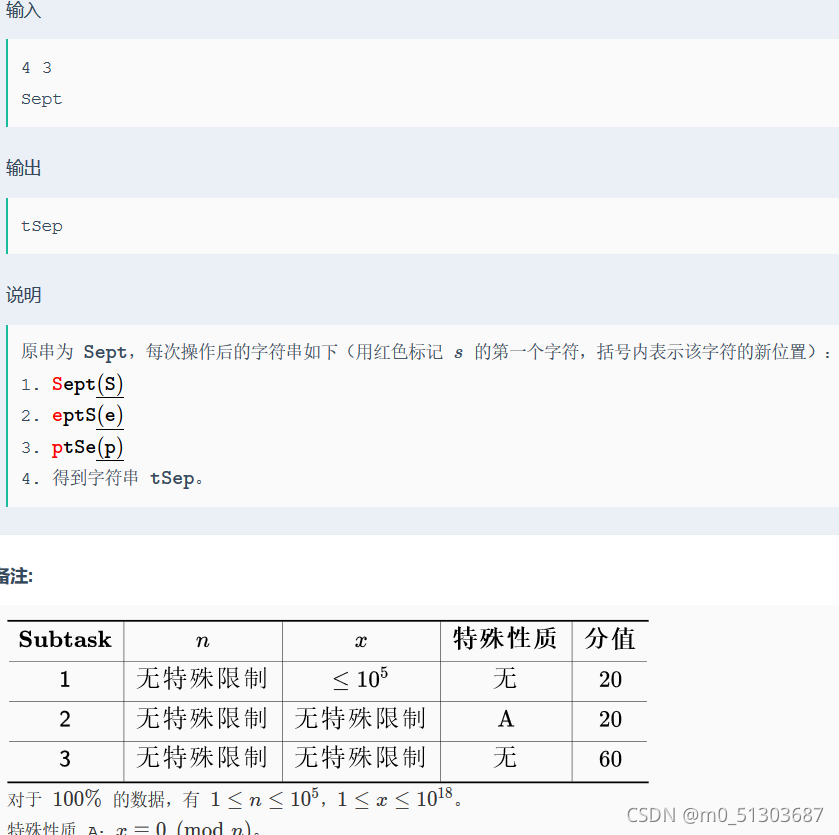
这题很简单，不难发现操作会形成循环。所以有效次数为x mod n，直接模拟即可。

#include <iostream>
#include <string>
using namespace std;
int main() {
    ios::sync_with_stdio(false);
    string s;
    long long len,x;
    cin>>len>>x;
    cin>>s;
    x%=len;
    for(int i=0; i<x; i++) {
    	//s=s[0]+s.substr(1)  不能这样写
        s.append(1,s[0]);
        s=s.substr(1);
    }
    cout<<s;
    return 0;
}

2.


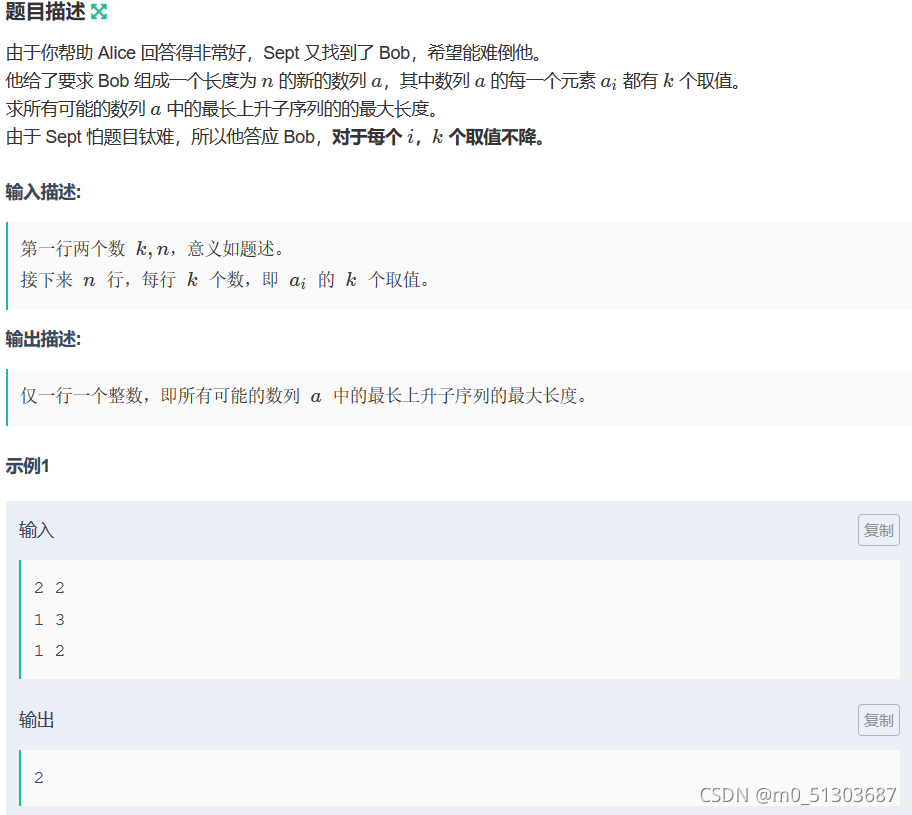
这题没有正确思路，我是这样想的：枚举LIS的可能的起始位置，并选其第一个元素，第i个元素是对应序列中第一个比第i-1个元素大的值。如果找不到，则认为是对应序列的最后一个值。
这其实是贪心的思路，其实我原本想骗一小部分分，没想到对了70%……正解思路DP暂时不太懂，以后有时间慢慢磨把。

//错误代码
#include <cstdio>
#include <algorithm>
#include <vector>
const int MAXN=1001,MAXK=5001;
using namespace std;
int a[MAXN],n;
vector<int> b[MAXN];
int lis() {
	vector<int> dp(n+2);
	vector<int>::iterator it=dp.begin();
	dp[1]=a[1];
	int len=1;
	for(int i=2; i<=n; i++) {
		if(a[i]>dp[len]) {
			dp[++len]=a[i];
		}
		else {
			int loc=lower_bound(it+1,it+len+1,a[i])-it;
			dp[loc]=a[i];
		}
	}
	return len;
}

int main() {
    int k,res=0;
    scanf("%d%d",&k,&n);
    for(int i=1; i<=n; i++) {
    	for(int j=0; j<k; j++) {
    		int x;
    		scanf("%d",&x);
    		b[i].push_back(x);
		}
	}
	for(int i=1; i<=n; i++) {  //枚举LIS的起始位置
		a[i]=b[i][0];
		for(int j=i+1; j<=n; j++) {
			int loc=upper_bound(b[j].begin(),b[j].end(),a[j-1])-b[j].begin();
			if(loc==(int)b[j].size()) 	a[j]=b[j][0];
			else	a[j]=b[j][loc];
		}
		res=max(res,lis());
	}
	printf("%d",res);
    return 0;
}

3.

暴力BFS竟然能通过，说明此题数据够水啊……正解是倒着建边正序遍历，这样每个点只经过一次。与我写的这篇博客里的第二题类似。可以用std::set完成题目中要求的去重与排序工作。

#include <cstdio>
#include <algorithm>
#include <set>
#include <queue>
const int M=100001;
using namespace std;
struct graph {
    int next,to;
    graph():next(-1),to(-1) {}
    graph(int n,int t):next(n),to(t) {}
};
vector<graph> G;
int fir[M],n;
inline void add(int u,int v,int &i) {
    G.push_back(graph(fir[u],v));
    fir[u]=i++;
}
bool vis[M];
inline void bfs(int st) {  //返回能到达的最小的点
    int res=st;
    queue<int> q;
    q.push(st);
    while(!q.empty()) {
        st=q.front();
        q.pop();
        vis[st]=1;
        res=min(res,st);
        for(int i=fir[st]; ~i; i=G[i].next) {
            int to=G[i].to;
            if(!vis[to]) {
                q.push(to);
            }
        }
    }
}

int main(){
    int m,k=0;
    set<int> res;
    scanf("%d%d",&n,&m);
    fill(fir+1,fir+n+1,-1);
    for(int i=0; i<m; i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        add(v,u,k);
    }
    for(int i=1; i<=n; i++) {
    	if(!vis[i]) {
    		bfs(i);
    		res.insert(i);
		}
	}
    set<int>::iterator it=res.begin();
    printf("%d",*it);
    while(++it!=res.end()) {
        printf(" %d",*it);
    }
    return 0;
}

4.


这其实是上一次周赛的第四题，不过由于本次的不会做而且题解也看不懂，所以换成这个。
这题正解是floyed。op=1时说明x点“通”了，任何点都可以通过x点中转，此时以x点为中转点进行floyed即可。注意为了降低复杂度，已经“通”的点就不要再遍历了。注意要对起点先跑一遍。
op=2时，根据题意输出即可。注意更新起点。

#include <cstdio>
#include <algorithm>
#define INF 0x3f3f3f3f
const int M=301;
using namespace std;
int G[M][M];
bool xd[M];
void floyed(int n,int mid) {
    for(int i=1; i<=n; i++) {
        for(int j=1; j<=n; j++) {
            G[i][j]=min(G[i][j],G[i][mid]+G[mid][j]);
        }
    }
}

int main() {
    int n,m,s,q;
    scanf("%d%d%d%d",&n,&m,&s,&q);
    for(int i=1; i<=n; i++) {
        fill(G[i], G[i]+n+1,INF);
        G[i][i]=0;
    }
    for(int i=0; i<m; i++) {
        int u,v,w;
        scanf("%d%d%d",&u,&v,&w);
        if(u!=v)    G[u][v]=min(G[u][v], w);
    }
    floyed(n, s);
    xd[s]=1;
    for(int i=0; i<q; i++) {
        int op,x;
        scanf("%d%d",&op,&x);
        if(op==1) {
            if(!xd[x]) {
                xd[x]=1;
                floyed(n, x);
            }
        }
        else if(op==2) {
            if(!xd[x]||G[s][x]==INF)    printf("-1\n");
            else {
                printf("%d\n",G[s][x]);
                s=x;
            }
        }
    }
    return 0;
}