1、寻找数组的中心索引
给你一个整数数组 nums ,请计算数组的 中心下标 。
数组 中心下标 是数组的一个下标,其左侧所有元素相加的和等于右侧所有元素相加的和。
如果中心下标位于数组最左端,那么左侧数之和视为 0 ,因为在下标的左侧不存在元素。这一点对于中心下标位于数组最右端同样适用。
如果数组有多个中心下标,应该返回 最靠近左边 的那一个。如果数组不存在中心下标,返回 -1 。
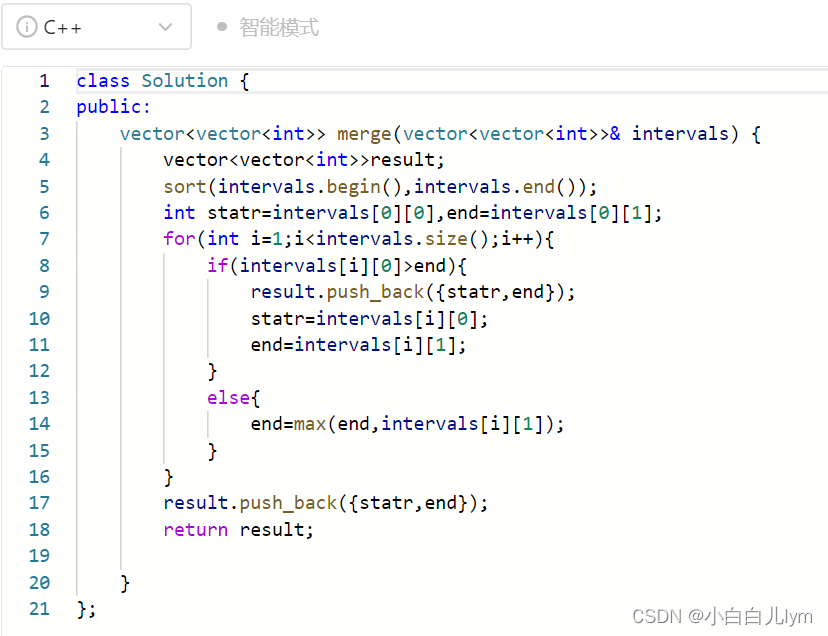
分析:先求出数组总和sums,左边元素之和设为sums_left,遍历循环,右边元素sums_right=sums-sums_left-nums[i],即当满足2*sums_right+nums[i]=sums时,nums[i]的索引i即是中心索引。
2、搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
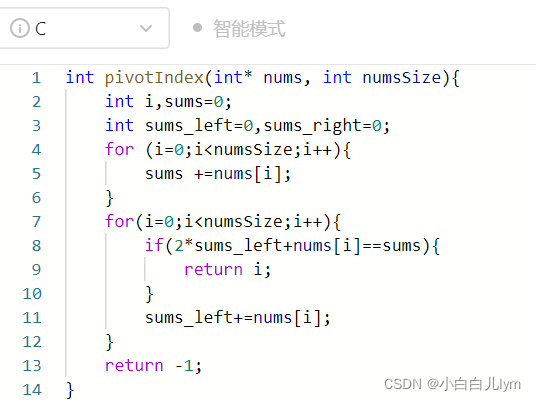
①for循环依次遍历寻找到大于或等于目标值的位置直接返回。时间复杂度为O(n)
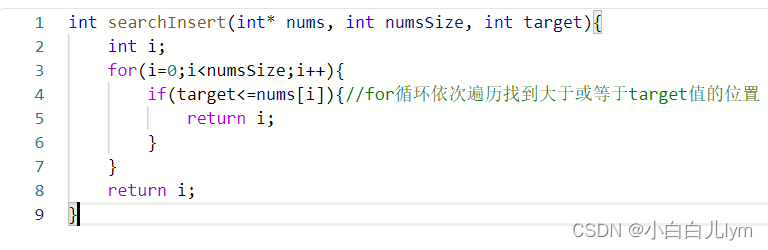
②二分查找,时间复杂度为 O(log n) 。
分析:设左右边界left和right,设中间元素下标mid,不断压缩数组长度numsSize,调整左右边界,查到找到目标值位置,返回元素下标。
3、合并区间
以数组 intervals 表示若干个区间的集合,其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间,并返回 一个不重叠的区间数组,该数组需恰好覆盖输入中的所有区间 。
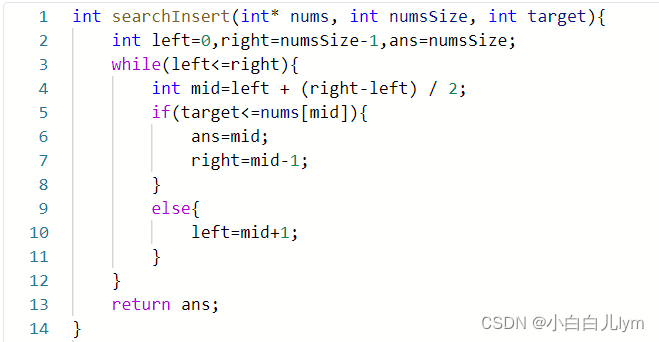
分析:先定义一个结果数组result,对原始数组集合进行排序,定义并初始化新区间的左右边界(为原始数组集合中的第一个数组),从原始数组集合中的第二个数组开始遍历,如果该区间的左边界大于新区间的右边界,则两数组没有重合,直接将该区间的左右边界加入到结果数组,并更新结果数组的左右边界。若有重叠则将结果区间的右边界更新为新区间和原始区间的最大值。循环遍历结束时,将当前左右边界构成的新区间加入到结果数组,并返回。