matlab傅里叶级数_matlab实现傅里叶级数展开

clear all;clc;syms t;y = 1+sin(100*t);T0=2*pi/100;N=5;  %% N个谐波figure(1)subplot(211)ezplot(y,[0,0.25]);grid on;xlabel('t(sec)');ylabel('y(t)');%% x is periodic signal & T0 is period & N is number of harmonic%% 自建求解傅里叶系数函数的function[Y1,w1]=fourierseries(y,T0,N);Y=[conj(fliplr(Y1(2:N))) Y1];w = [-fliplr(w1(2:N)) w1];%% 对于实值信号，傅里叶系数的模是偶函数，相位是奇对称的subplot(223)stem(w,abs(Y));grid on; axis([-400 400 -0.1 1.1]);xlabel('k\Omega_0(rad/sec)');ylabel('|Y_k|');subplot(224)stem(w,angle(Y));grid on; axis([-400 400 -2 2]);xlabel('k\Omega_0(rad/sec)');ylabel('\angle(Y_k)');function[X,w] = fourierseries(x,T0,N)syms t;for k = 1:N,    X1(k)=int(x*exp(-j*2*pi*(k-1)*t/T0),t,0,T0)/T0;    %%只求出k>=0的信号幅度谱和相位谱，看k<0的利用对称性求出    X(k)=subs(X1(k));    w(k)=(k-1)*2*pi/T0;endend

程序用到的性质

1. 对于实值信号，傅里叶系数的模是偶函数，相位是奇对称的；

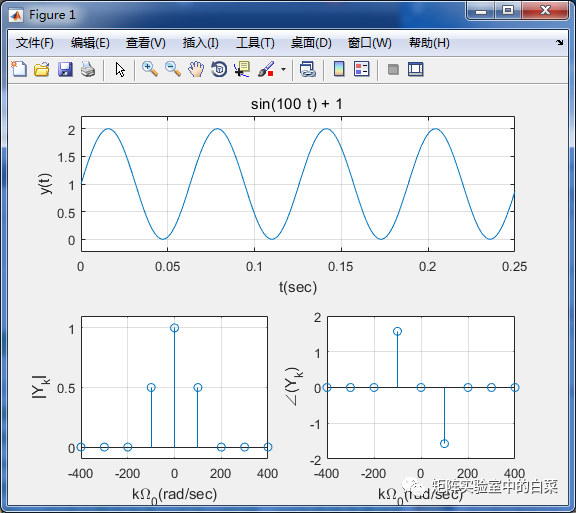
结果图：