2021-12-13 集成模型

第八章——集成模型

8.1 集成模型和它的优势
8.2 集成模型的稳定性
8.3 随机森林的训练
8.4 随机森林的过拟合

8.1 集成模型和它的优势

1、什么是集成模式

• 单个学习器要么容易欠拟合要么容易过拟合，为了获得泛化性能优良的学习器，可以训练多个个体学习器，通过一定的结合策略，最终形成一个强学习器。这种集成多个个体学习器的方法称为集成学习(ensemble learning)。

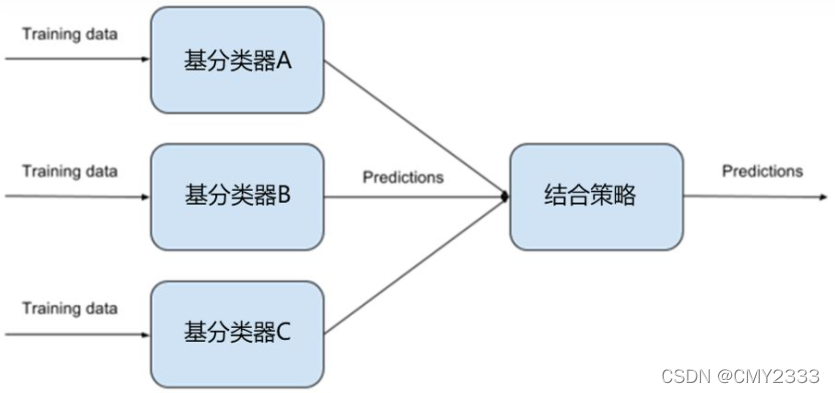
• 几乎对于所有分类问题，集成模型大都是首选，主要是因为它的效果很好且稳定，另外这些模型也比深度学习模型的可解释性好。
• 可解释性好：随机森林或升树模型基于决策树，决策树模型的可解释性很好，而且集成模型可简单理解为是决策树的集合。

2、集成模型的优势

• 具有高准确率、不容易过拟合，有很好的抗噪声能力，对异常点离群点不敏感、实现简单，训练速度快，可以得到变量重要性排序。
• 集成模型的两大类：Bagging（随机森林）、Boosting（GBDT、XGBoost）

3、构造集成模型

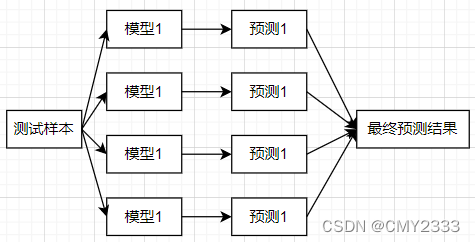
• 基于Bagging的预测：训练时每个模型都是相互独立进行训练的；训练完后每个模型都可以参加决策。最终结果等同于做了个平均的操作，这点跟Boosting有很大的区别。

8.2 集成模型的稳定性

1、方差和稳定性

• 为了模型具有较强的泛化能力，需要解决过拟合问题，而不稳定模型容易过拟合（在训练数据上表现很好，但放在真实线上环境就不行）。
• 方差可以表示模型的稳定性。集成模型可以减少方差。
• 假如有N个模型，每个模型在预测时的方差为 σ^2， 则通过N个模型一起预测的方差是：(σ^2)/N。

8.3 随机森林的训练

1、随机森林的核心思想

• 随机森林是通过多棵决策树共同做决策的。
  

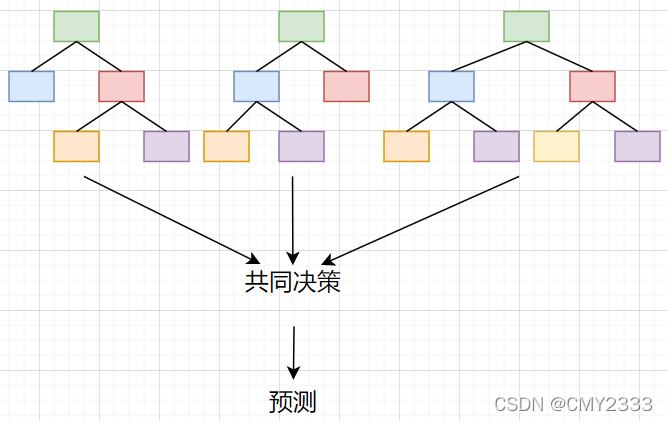
2、随机森林的构造

• 构造随机森林需要考虑：
  ① 只需要一份训练数据；
  ② 确保多棵决策树要优于单颗决策树；
• 问题：稳定性的基础是多样性(Diversity)，如果得出的多棵决策树之间相关性比较大，稳定性和效果就不太好。
• 如何构造出很多具备多样性的决策树？
  答：训练样本的随机性、 特征选择时的随机性。

8.4 随机森林的过拟合

1、随机森林的参数

• 随机森林对避免过拟合的问题表现不错，但这并不代表它不会过拟合，目前的解决方法主要还是调参。
• 函数sklearn.ensemble.RandomForestClassifier参数参考