单向环形链表(约瑟夫问题) 1

单向环形链表

开始前我们先介绍一下Josephu(约瑟夫)问题:
设编号为1,2,3…n个人围坐在一圈,约定编号为k(1<=k<=n)的人开始报数,数到m的人出列,它的下一位又从1开始报数,数到m的人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列.

让我们先来假设有5个人,编号为1的人开始报数,数到2的人出列,这个时候出队的编号的序列是多少呢?
我们先画一个图:

这里 1 2 3 4 5分别代表这5个人,第一个出队的应该为 2;
然后就变成了

这个时候应该3号开始喊1,所以第二个出队列的应该是4;
依次类推,我们不难分析出出队顺序应该为:
2 --> 4 -->1 -->5 -->3 ;

但是当n,k,m变大之后呢?我们应该怎么样用代码去实现这个过程?
这里就是要用到我们今天要说的单向环形链表了.

构建一个单向环形链表的思路:
1.先创建第一个节点,让filst指向该节点,并形成环形
2.后面我们每当创建一个新节点,就把该节点加入到已有的环形链表中.

遍历环形链表:
1.先让一个辅助变量指向first节点;
2.然后通过一个while循环遍历该链表即可(当node.next==first即可结束循环)

代码如下:

//创建一个环形的链表
class CircleSingleLinkedList {
    //先初始化一个frist节点
    private Node frist = new Node(-1);

    //添加节点的方法(nums相当于问题中的n)
    public void add(int nums) {
        //nums 做一个校验
        if (nums < 1) {
            System.out.println("nums值不正确");
            return;
        }
        Node temp = null;
        //使用for循环来创建我们的链表
        for (int i = 1; i <= nums; i++) {
            //根据标号,创建节点
            Node node = new Node(i);
            //如果是第一个小孩,
            if (i == 1) {
                frist = node;
                frist.next = frist;//构成环
                temp = frist; //因为frist不能动,构建一个辅助节点指向frist
            } else {
                temp.next = (node);
                node.next = (frist);
                temp = node;
            }

        }
    }

    //遍历当前环形链表
    public void show() {
        //先判断链表是否为空
        if (frist.val == -1) {
            System.out.println("链表为空");
            return;
        }
        //因为frist不能动,因此我们热然使用辅助指针
        Node temp = frist;
        //当temp.next == frist时说明遍历完毕(但是当链表只有一个元素时,无法遍历,因此要做特殊处理)
        while (temp.next != frist) {
            System.out.println("编号:" + temp.val);
            temp = temp.next;
        }
        if (temp.next == frist) { //特殊处理
            System.out.println("编号:" + temp.val);
        }
    }
    
class Node {
    public int val;
    public Node next;//指向下一个节点

    public Node(int val) {
        this.val = val;
    }

    @Override
    public String toString() {
        return "Node{" +
                "val=" + val +
                '}';
    }
}

接下来让我们对上面的代码进行一个测试:

public class Josephu {
    public static void main(String[] args) {
        CircleSingleLinkedList cl = new CircleSingleLinkedList();
        cl.show();   //不添加元素进行遍历
        System.out.println("|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||");
        CircleSingleLinkedList cl1 = new CircleSingleLinkedList();
        cl1.add(1);
        cl1.show();   //添加一个元素进行遍历
        System.out.println("|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||");
        CircleSingleLinkedList cl2 = new CircleSingleLinkedList();
        cl2.add(15);
        cl2.show();   //添加15个元素进行遍历
        System.out.println("|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||");
    }
}

让我们来看一下结果: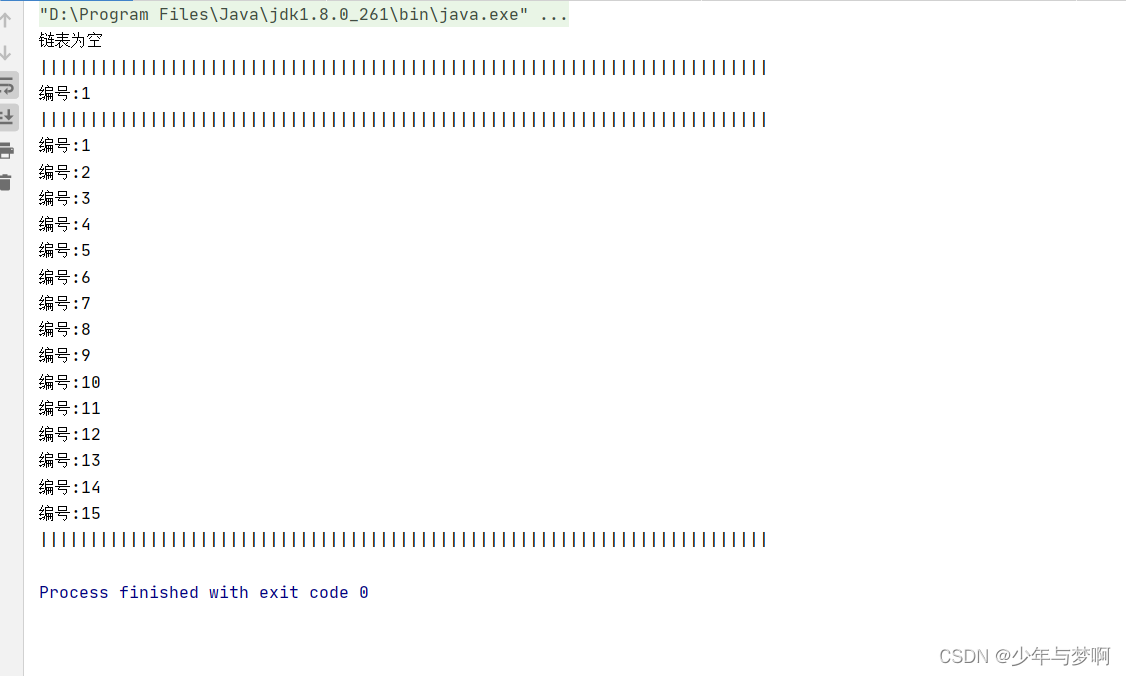

这是没有问题的.接下来我们来说一下运用环形链表解决约瑟夫问题.