1315 网格（卡特兰数，分解质因数）

1. 问题描述：​​​​​​​ 

某城市的街道呈网格状，左下角坐标为 A(0，0)，右上角坐标为 B(n，m)，其中 n ≥ m。现在从 A(0，0) 点出发，只能沿着街道向正右方或者正上方行走，且不能经过图示中直线左上方的点，即任何途径的点 (x，y) 都要满足 x ≥ y，请问在这些前提下，到达 B(n，m) 有多少种走法。

输入格式

仅有一行，包含两个整数 n 和 m，表示城市街区的规模。

输出格式

输出一个整数，表示不同的方案总数。

数据范围

1 ≤ m ≤ n ≤ 5000

输入样例：

6 6

输出样例：

132
来源：https://www.acwing.com/problem/content/1317/

2. 思路分析：

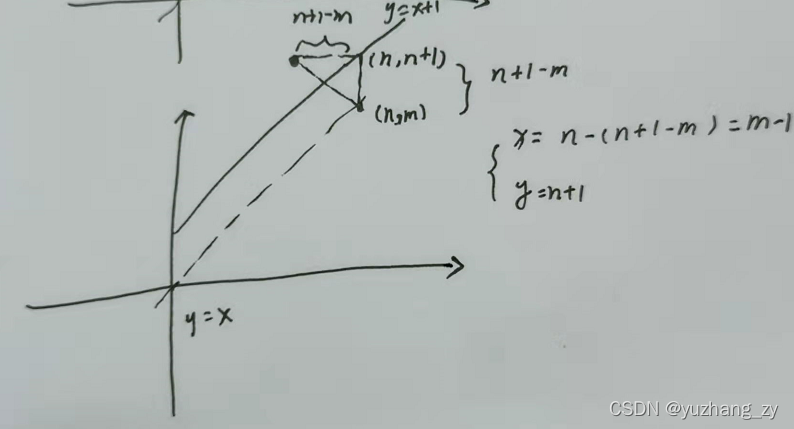
分析题目可以知道这道题目属于卡特兰数的扩展，卡特兰数中最终是n * n的二维网格，这道题目是n * m的二维网格，其实也是类似的套路，我们需要做关于y = x + 1的对称得到与坐标(n，m)对称的坐标(x'，y')，可以根据几何关系得到(n，m)关于y = x + 1对称的坐标为(m - 1，n + 1)，所以最终的结果为Cn+m n - Cn+m m-1（与卡特兰数是一样的方法），因为题目中没有涉及到取模所以需要手写高精度。我们可以先用线性筛预处理一下1~100010之内的所有质数，当求解Cn+m n的时候其实是分解n + m！的质因数，n!的质因数，m!的质因数，使用一个get方法获取对应阶乘中当前质因子p的次数，相减的结果就等于当前Cn+m n结果中质因子为p的次数，然后使用高精度乘法将结果计算到数组a中，对于Cn+m m-1也是类似的方法，将结果存储到数组b中，最终使用高精度减法得到最终的结果。

3. 代码如下：

from typing import List


class Solution:
    # 使用全局的l记录当前高精度乘法的最大位数
    count = l = 0

    # 线性筛法求解1~n之间的质数, 方便后面分解质因数
    def init(self, n: int, primes: List[int], st: List[int]):
        for i in range(2, n):
            if st[i] == 0:
                primes[self.count] = i
                self.count += 1
            j = 0
            while primes[j] * i < n:
                st[primes[j] * i] = 1
                if i % primes[j] == 0:
                    break
                j += 1

    # 计算n!中有多少个质因子p
    def get(self, n: int, p: int):
        res = 0
        while n > 0:
            res += n // p
            n //= p
        return res

    # 高精度乘法
    def mul(self, r: List[int], p: int):
        t = 0
        for i in range(self.l):
            t += r[i] * p
            r[i] = t % 10
            t //= 10
        while t > 0:
            r[self.l] = t % 10
            t //= 10
            self.l += 1
    
    # 求解Cxy的结果并将结果存储到r中
    def C(self, r: List[int], x: int, y: int, primes: List[int]):
        r[0] = 1
        self.l = 1
        for i in range(self.count):
            p = primes[i]
            # 计算当前阶乘中所包含的质因子的次数
            s = self.get(x, p) - self.get(y, p) - self.get(x - y, p)
            while s:
                self.mul(r, p)
                s -= 1
        return self.l

    # 高精度减法
    def sub(self, a: List[int], al: int, b: List[int], bl: int):
        t = 0
        for i in range(al):
            a[i] -= (t + b[i])
            if a[i] < 0:
                a[i] += 10
                t = 1
            else:
                t = 0

    def process(self):
        n, m = map(int, input().split())
        N = 100010
        primes, st = [0] * N, [0] * N
        self.init(N, primes, st)
        a, b = [0] * N, [0] * N
        al = self.C(a, n + m, n, primes)
        bl = self.C(b, n + m, m - 1, primes)
        # 将结果存储到列表a中
        self.sub(a, al, b, bl)
        i = al - 1
        while i >= 0 and a[i] == 0: i -= 1
        while i >= 0:
            print(a[i], end="")
            i -= 1


if __name__ == '__main__':
    Solution().process()