有统计说，它是最高效、最常用的字符串匹配算法。要说最知名的一种的话，那就非KMP算法莫属。

问题：如何借助上一节BM算法的讲解思路，让你能更好地理解KMP算法？

1. KMP算法基本原理

1.1 基本概念

好前缀和坏字符。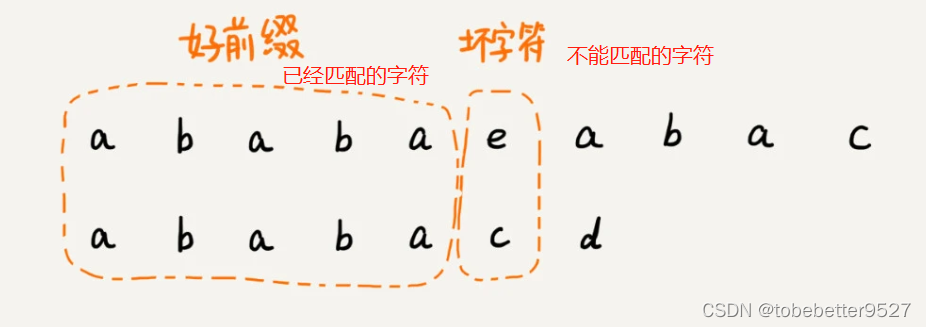

好前缀的后缀子串，模式串的前缀子串。

最长可匹配后缀子串，最长可匹配前缀子串。

1.2 滑动的位数

1.3 如何求好前缀的最长可匹配前缀和后缀子串

提前构建一个数组，用来存储模式串中每个前缀（这些前缀都有可能是好前缀）的最长可匹配前缀子串的结尾字符下标。我这个数组定义为next数组，也叫失效函数（failure function）。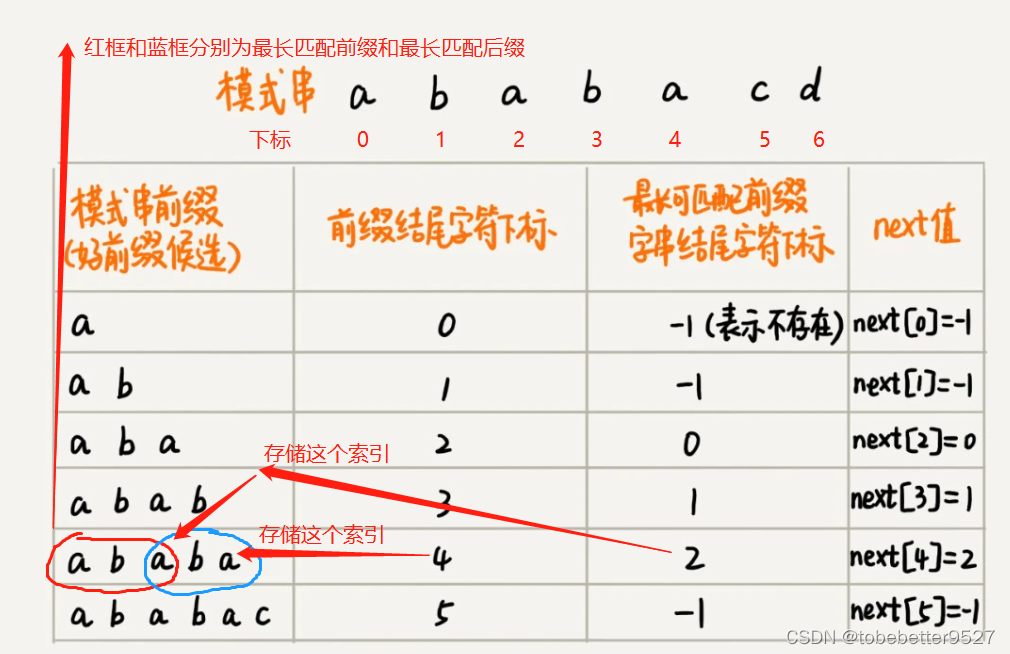

2. KMP代码实现

// a, b分别是主串和模式串；n, m分别是主串和模式串的长度。
public static int kmp(char[] a, int n, char[] b, int m) {
  int[] next = getNexts(b, m);
  int j = 0;
  for (int i = 0; i < n; ++i) {
    while (j > 0 && a[i] != b[j]) { // 一直找到a[i]和b[j]
      j = next[j - 1] + 1;
    }
    if (a[i] == b[j]) {
      ++j;
    }
    if (j == m) { // 找到匹配模式串的了
      return i - m + 1;
    }
  }
  return -1;
}

3. next数组计算过程

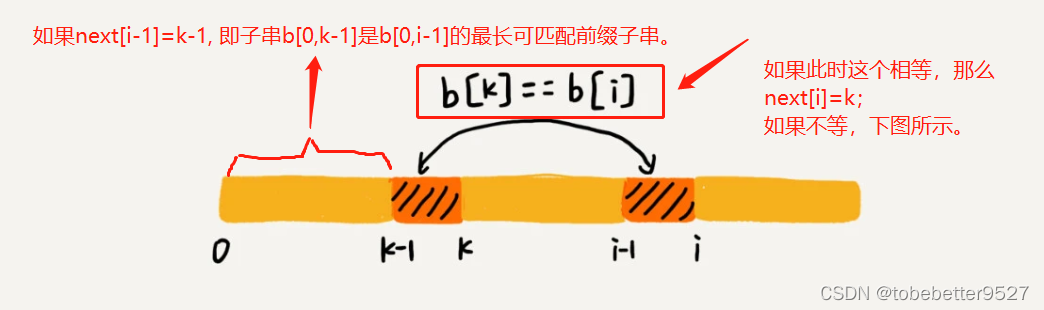
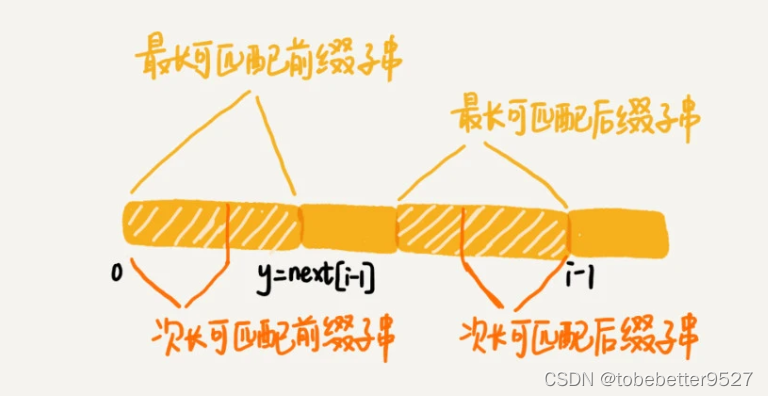
不好很好懂，看下面的例子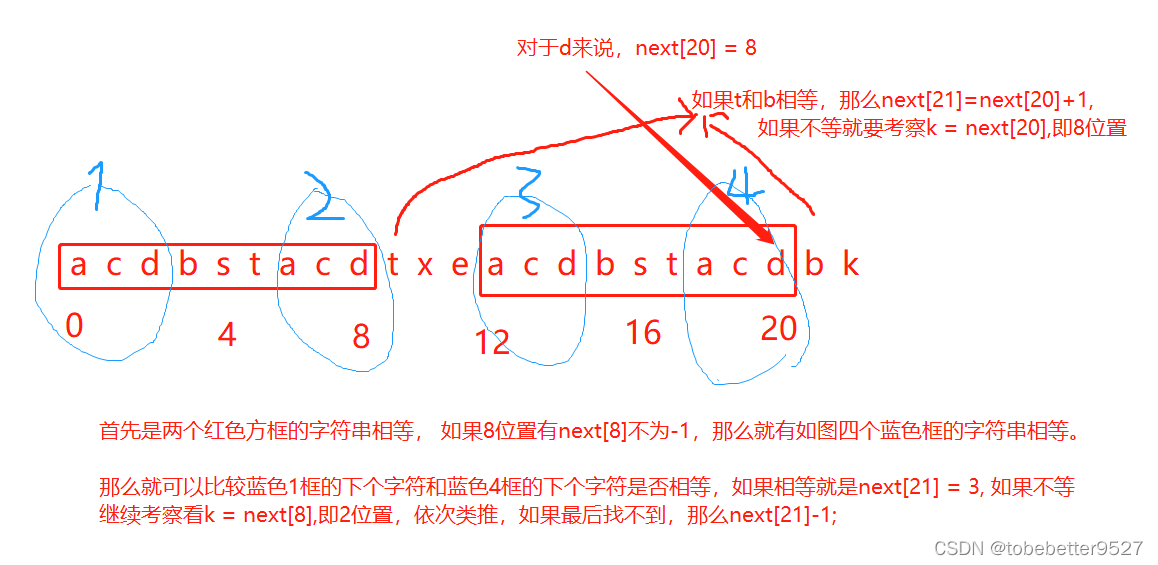

// b表示模式串，m表示模式串的长度
private static int[] getNexts(char[] b, int m) {
  int[] next = new int[m];
  next[0] = -1;
  int k = -1;
  for (int i = 1; i < m; ++i) {
    while (k != -1 && b[k + 1] != b[i]) {
      k = next[k];
    }
    if (b[k + 1] == b[i]) {
      ++k;
    }
    next[i] = k;
  }
  return next;
}

4. KMP算法复杂度分析

• 空间复杂度是O(m)，只需要一个额外的next数组。
• 时间复杂度O(m+n)。