问题描述

给定一个字符串,求字符串中字典序最大的子序列.字典序最大的子序列是这样构造的:给定一个字符串 $a_0{a}_1...a_{n-1}$ ,首先在字符串中找到值最大的字符 $a_i$,然后在剩余的字符串 $a_{i+1}{a}_{i+2}...a_n$中找到值最大的字符$a_j$,然后在剩余的字符串$a_{j+1}{a}_{j+2}...a_n$中找到值最大的字符$a_k$, $......$一直这样做下去,直到剩余字符串的长度为0为止.找到的字符按找到的顺序排成的字符串 $a_i{a}_j{a}_k...$就是我们要找的答案.

分析与解答

这个题目要解决,就得了解字典序的概念.题目已经讲得比较明白了,所以一个很自然的想法,就是要多次遍历这个字符串,每一次找到字符串中的第一次出现的最大的元素,提取出来,将这个最大的元素的后缀作为下一次要遍历的字符串,同样地找到它最大的元素,不断这样遍历下去,就可以得到我们想要的字典序最大的子序列了.每次遍历得到的元素需要被保存,用largestSubStr来保存最后的字符串.

#给定一个字符串,求字符串中字典序最大的子序列.
def getLargestSubStr(strs):
	if strs == None:
		return
	largestSubStr = ""
	while len(strs) > 0:
		lens = len(strs)
		#最大数临时变量
		maxNum = -1
		#最大数下标临时变量
		maxIndex = 0
		for i in range(lens):
			if ord(strs[i]) > maxNum:
				maxNum = ord(strs[i])
				maxIndex = i
		largestSubStr += strs[maxIndex]
		strs = strs[maxIndex+1:]
	return largestSubStr
			
if __name__ == "__main__":
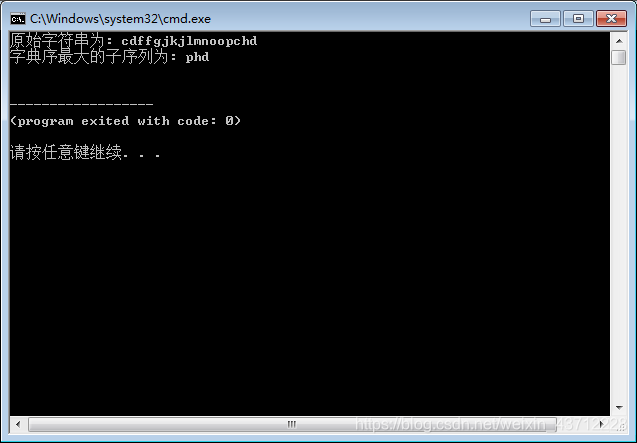
	strs = "cdffgjkjlmnoopchd"
	lstrs = getLargestSubStr(strs)
	print("原始字符串为:", str(strs))
	print("字典序最大的子序列为:", str(lstrs))

我们称这样的方法为顺序遍历法.顾名思义,它是按照索引增加的顺序来遍历字符串的,每次遍历都会得到一个最大的元素.这里为了简便,就都给的是字母字符,事实上其他字符也可以.它们之间的大小关系比较要借助到它们所对应的ASCII码,也就是具体的数字比较.关于字母的ASCII码范围请自行百度.这里不再归纳.算法的时间复杂度大小跟字符串本身有很大关系,如果这个字符串的字符是按照逆序排列的,那么可想而知,最外层的循环"while len(strs) > 0:“就相当于每次len(strs)减一,其时间复杂度为O(len(strs)),设len(strs) = N, 即O(N).内层循环由于是for循环(for i in range(lens)?,它的时间复杂度是固定的,即O(N).所以整个算法的时间复杂度在这种情况下是$O(N^2)$.而最好的情况下,就只要遍历一次strs就可以跳出外层while循环,所以是O(N).差别很大.如果碰巧不幸这个字符串的大部分元素都是逆序排列的,其时间复杂度也是很大的.所以有没有比较稳定的算法,它不依赖于字符串的结构,即在任何情况下它的时间的复杂度都是线性或者接近线性的呢?这就要讲到另一种想法:逆序排序法了.
不知道大家有没有发现,这种问题的答案字符串一定会包含原字符串的最后一个元素.因为它总是对这个字符串的后缀找最值,如果最值不是最后的元素,那么字符串的后缀就永远包含它.由于字符串的长度有限,所以最终一定能够使得后缀长度为1,也就是字符串的最后一个元素.又或者在这个情况发生之前,这个元素在某个后缀数组中是最大的,这个时候也就没有后缀,即算法终止于此.所以我们说,无论是什么样的情况,字符串的最后一个元素一定会出现在新的字符子串中,且一定在最后一个位置.
我们又注意到,字典序最大的子序列里元素排列是逆序的,比如说"edcb"就可能是字典序最大的子序列,但要是有一个字符违反了这个逆序排列的原则,这样得到的子序列一定不是字典序最大的子序列,比如"edcdb”,因为c<d所以这个子序列一定不是.根据这个原则,我们就可以采取这样的思路:首先最后一个字符一定是的,我么倒过来找,但凡找到比这个字符大的字符,就添到我们的largestSubStr这个空字符串中,前面说这个子序列如果按照顺序遍历一定是逆序排列的,那么反过来它一定是正序排列的.又因为这个子序列一定是首字符最大的,那么反过来我们逆序得到的也就是末尾字符最大.这也就是说,我们逆序查找,只要查找的字符比当前largestSubStr中新添加的字符大,我么就把这个字符添加进去largestSubStr.然后当字符串遍历完成后事实上我们的算法也就可以停止了.接下来只要把largestSubStr字符串翻转过来就好了.这个算法的时间复杂度显然是O(N)的,因为它只有一个循环嘛.

#给定一个字符串,求字符串中字典序最大的子序列.
#方法2:逆序遍历法
def getLargestSubStr(strs):
	if strs == None:
		return
	#首先将字符串翻转过来
	strs = strs[::-1]
	#将第一个元素(也就是原字符串末尾元素)添加到largestSubStr中去
	largestSubStr = strs[0]
	#保存最大数的临时变量
	maxNum = ord(strs[0])
	lens = len(strs)
	for i in range(1, lens):
		if ord(strs[i]) > maxNum:
			maxNum = ord(strs[i])
			largestSubStr += strs[i]
	#将得到的字符串翻转过来才是实际的字典序最大的子序列
	largestSubStr = largestSubStr[::-1]
	return largestSubStr
			
if __name__ == "__main__":
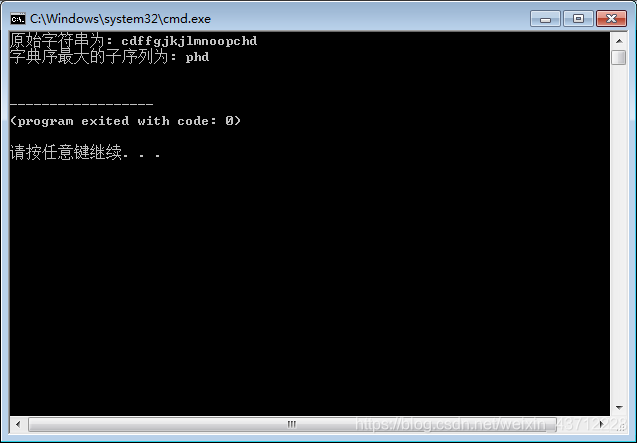
	strs = "cdffgjkjlmnoopchd"
	lstrs = getLargestSubStr(strs)
	print("原始字符串为:", str(strs))
	print("字典序最大的子序列为:", str(lstrs))

以上.