优点
(1) 从计算的角度上, Sigmoid和Tanh激活函数均需要计算指数, 复杂度
高, 而ReLU只需要一个阈值即可得到激活值。
(2) ReLU的非饱和性可以有效地解决梯度消失的问题, 提供相对宽的激活
边界。
(3) ReLU的单侧抑制提供了网络的稀疏表达能力。
局限性
ReLU的局限性在于其训练过程中会导致神经元死亡的问题。 这是由于函数
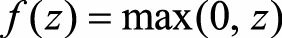
导致负梯度在经过该ReLU单元时被置为0, 且在之后也不被任何数
据激活, 即流经该神经元的梯度永远为0, 不对任何数据产生响应。 在实际训练中, 如果学习率(Learning Rate) 设置较大, 会导致超过一定比例的神经元不可逆死亡, 进而参数梯度无法更新, 整个训练过程失败。
为解决这一问题, 人们设计了ReLU的变种Leaky ReLU(LReLU) , 其形式表示为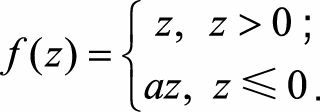
ReLU和LReLU的函数曲线对比如图9.9所示。 LReLU与ReLU的区别在于,
当z<0时其值不为0, 而是一个斜率为a的线性函数, 一般a为一个很小的正常数,这样既实现了单侧抑制, 又保留了部分负梯度信息以致不完全丢失。 但另一方面, a值的选择增加了问题难度, 需要较强的人工先验或多次重复训练以确定合适的参数值
基于此, 参数化的PReLU(Parametric ReLU) 应运而生。 它与LReLU的主要区别是将负轴部分斜率a作为网络中一个可学习的参数, 进行反向传播训练, 与其他含参数网络层联合优化。 而另一个LReLU的变种增加了“随机化”机制, 具体地, 在训练过程中, 斜率a作为一个满足某种分布的随机采样; 测试时再固定下来。 Random ReLU(RReLU) 在一定程度上能起到正则化的作用。
参考文献:百面机器学习
版权声明:本文为gubeiqing原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明。