101.对称二叉树
给定一个二叉树，检查它是否是镜像对称的。

一、对称二叉树理论

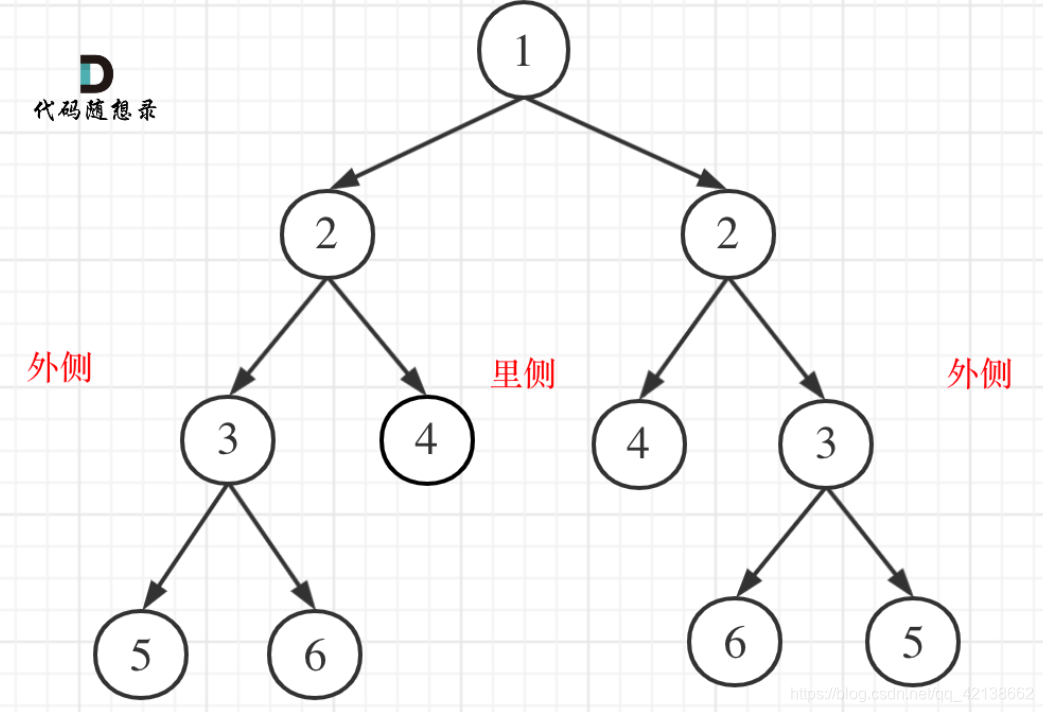
对称二叉树如图所示，要判断一个二叉树是否为对称二叉树，实际上就是要判断根节点的左右两个子树是否镜像对称。因此，其解决方案为：按照对称的方式遍历左右子树，比较同时遍历的节点是否一致。而且在遍历过程中，只有两个子树的根节点对称了，继续比较左右子树是否对称才有意义，因此我们使用"中序遍历"（其实不是严格的中序遍历，只是我们先比较根节点）

按照遍历依赖的不同，可以分为以下三类方法：

1. 递归法
2. 基于队列的迭代法
3. 基于栈的迭代法

• 实测递归法最快最简洁
  

二、对称二叉树解题代码

1、递归法

class Solution {
public:
	//这里的left和right可以视作处于对称位置的两个子树的根节点
    bool isequal(TreeNode* left, TreeNode* right){
    	
    	//首先比较根节点是否一致，如果根节点不一致，就没必要继续比较了，终止递归返回false
    	//如果根节点均为空，说明也没必要继续比较了，终止递归返回true
    	//注意要先处理根节点为null的情况，只有根节点不为null，才能使用->val
        if(left == nullptr && right == nullptr) return true;
        else if(left == nullptr && right != nullptr || left != nullptr && right == nullptr) return false;
        else if(left->val != right->val) return false;

		//当根节点对称时，递归比较根节点左右子树是否对称，注意这里两个子树的对应关系，应该是外侧等于外侧，内侧等于内侧
        bool outside = isequal(left->left, right->right);
        bool inside = isequal(left->right, right->left);

		//当左右子树也对称时候，返回以left和right为根节点的两个子树对称
        bool res = inside && outside;
        return res;
    }
    bool isSymmetric(TreeNode* root) {
    	//处理空树情况
        if(root == nullptr) return true;
        //递归比较左右子树是否对称
        return isequal(root->left, root->right);
    }
};

2、基于队列的迭代法

由于队列是先入先出，每次比较对称都是先比较一层是否对称，然后再比较下一层，可是视作"层序遍历"

class Solution {
public:
    bool isSymmetric(TreeNode* root) {

		//处理空树
        if (root == NULL) return true;

		//初始化队列，并初始化左右两个子树
        queue<TreeNode*> que;
        que.push(root->left);   // 将左子树头结点加入队列
        que.push(root->right);  // 将右子树头结点加入队列
        
        while (!que.empty()) {  // 接下来就要判断这这两个树是否相互翻转

			//首先判断根节点是否符合反转
            TreeNode* leftNode = que.front(); que.pop();
            TreeNode* rightNode = que.front(); que.pop();
            // 左节点为空、右节点为空，此时说明是对称的，且不需要继续处理
            if (!leftNode && !rightNode) {  
                continue;
            }
            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            //这里这个写是||首先判断前面的条件，有一个为1就停止判断，因此不会出现无效指针解引用
            if ((!leftNode || !rightNode || (leftNode->val != rightNode->val))) {
                return false;
            }

			//如果跟节点符合反转，按照对称顺序压入两个根节点的孩子节点
            que.push(leftNode->left);   // 加入左节点左孩子
            que.push(rightNode->right); // 加入右节点右孩子
            que.push(leftNode->right);  // 加入左节点右孩子
            que.push(rightNode->left);  // 加入右节点左孩子
        }
        return true;
    }
};

3、基于栈的迭代法

基于栈的迭代法和基于队列的迭代法一样，直接将队列换成栈就可以。只是栈是先进后出，因此此时不再是层次遍历，而是“深度优先遍历”。

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        stack<TreeNode*> sta;
        if(root != nullptr){
            sta.push(root->left);
            sta.push(root->right);
            while(!sta.empty()){
                TreeNode* left = sta.top();
                sta.pop();
                TreeNode* right = sta.top();
                sta.pop();

                if(left == nullptr && right == nullptr) continue;
                else if(left != nullptr && right == nullptr || left == nullptr && right != nullptr) return false;
                else if(left->val != right->val) return false;

                sta.push(left->left);
                sta.push(right->right);
                sta.push(left->right);
                sta.push(right->left);
            }
        }
        return true;
    }
};

三、相关题目

100. 相同的树
     给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

1、解题思路

与对称二叉树类似，只不过是比较的对象从两棵树对称位置的节点是否相同变成了两棵树相同位置的节点是否相同

2、解题代码

class Solution {
public:
    bool isSameTree(TreeNode* p, TreeNode* q) {
        if(p == nullptr && q == nullptr) return true;
        else if(p != nullptr && q == nullptr || p == nullptr && q != nullptr) return false;
        else if(p->val != q->val) return false;

        bool isleftsame = isSameTree(p->left, q->left);
        bool isrightsame = isSameTree(p->right, q->right);
        return isleftsame && isrightsame;
    }
};