CNN,作为一个经典的神经网络模型,我们并不陌生。CNN包含若干个卷积层和池化层。池化层相对简单,对于减少神经元数量,功不可没。而卷积层,才是我们理解的一个难点。
我们知道卷积层可以提取不同的特征。对CNN的训练,重点就是训练出来各种各样的卷积核来提取特征。初学者在学习CNN时,往往会面临一个问题,知道CNN的输出是如何计算的,也知道如何利用基于链式求导法则的反向传播算法去训练网络,却不知道为什么CNN能够提取图片特征,卷积核里面的那几个数字背后的意义和原理。
今天,我们就从特征提取来分析一下卷积核的作用。
一 对图像灰度的求导
提取特征,关键是要找到特征变化的分界点--特征的边缘。想象一下,特征的边缘具有什么特点? 边缘意味着两侧图像的灰度变化会很大。对数学比较敏感的同学,一提到变化,会想到导数。导数用来衡量变化率的大小,对于图像也是如此。下面是一个灰度变化的例子。
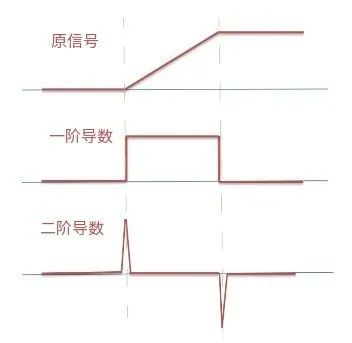
图中,原信号代表了原图象灰度的变化,第二行和第三行分别是对灰度的一阶导数和二阶导数。对比一阶导数图像和二阶导数图像,可以发现,二阶导数相比于一阶导数,对边缘有着更好的响应。因为对于灰度渐变区域,二阶导数可以识别出图像渐变区域的边缘。在实际中,我们可以根据实际情况来决定使用一阶导数还是二阶导数,在这里,我们用二阶导数来举例子。
当我们把图片的每一部分区域,依次带入到二阶导数时,对于灰度变化较小或者是均匀变化的区域,我们会得到一个接近0的值,而对于灰度变化大的区域,我们则会得到一个较大的值,从而识别出图片的边缘。
二 边缘提取
先看一个检测垂直边缘的例子。下图是一个矩形,我们希望过滤掉水平的上下边,而提取出垂直边。根据之前提到的,我们只需要计算水平方向上的梯度变化就可以。

水平方向一阶导数:
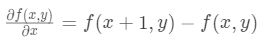
水平方向二阶导数:
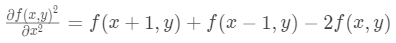
与之对应的卷积核:
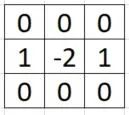
有时候,为了对应卷积的概念,会将卷积核沿对角线反转在做运算.在这里我们直接采用反转后的卷积核。
如果不明白为什么这个是与之对应的卷积核,不要慌,接着往下看。我们根据卷积计算的方法,来算一下。
我们首先从图片中取出一块3*3像素的图像,与卷积核进行运算。把中心点的坐标当作是x,y。那么四周的像素坐标也可以通过+1,或-1来得到。
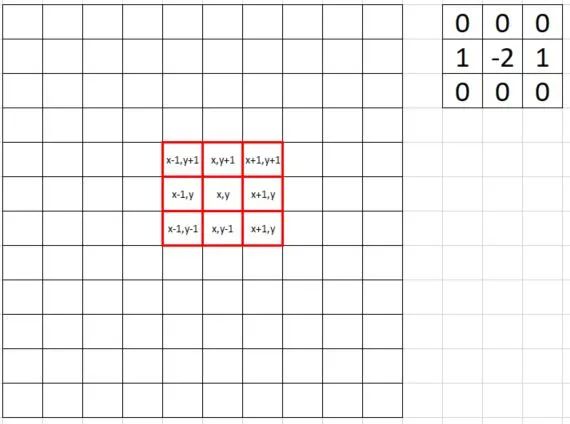
卷积后的结果为:
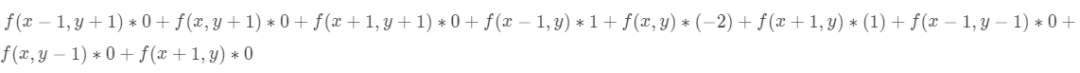
去除掉乘以0的项:
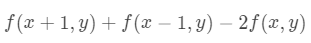
发现什么了吗?在与提取垂直边缘的卷积核运算后,得到的就是图像水平方向的二阶导数。当我们滑动卷积核来对整个图片卷积时,水平边缘就会令二阶导数取得一个接近于0的值,其余部分就会得到一个较大的值,从而突出了垂直边缘。
同理我们可以根据同时对水平方向与垂直方向,求二阶导数,得到可以同时提取水平边沿和垂直边沿的卷积核。
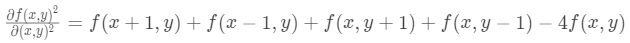
与之对应的卷积核:
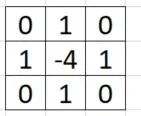
其实,这就是拉普拉斯算子。
在进一步扩展,任意方向的边沿提取
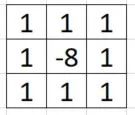
如果我们将提取出来的边缘,与原图叠加,实际上就是在原有的二阶导数基础上再叠加一次f(x,y),即卷积核变成:
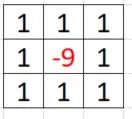
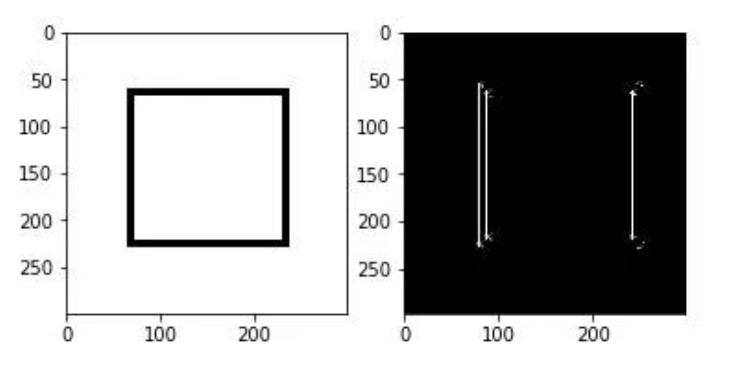
实际效果:
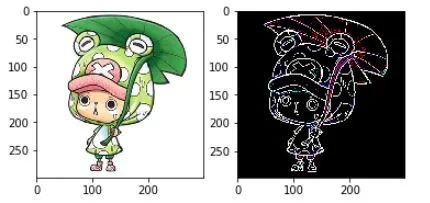
三 总结
在实际的应用中,我们不仅仅会只针对灰度来提取特征,还会用到颜色的变化,去提取不同的特征。当然卷积提取特征只是卷积核的功能之一,卷积还可以用来平滑图像噪点。有时候还会通过1*1的卷积核,通过加大step来起到降维的作用。