说明

python 内置pow函数用于实现幂的运算，在这里我使用的是快速幂算法实现pow函数功能。

快速幂

快速幂算法本质上基于的是分治思想。

优点：其时间复杂度为 O (log₂N)， 与暴力遍历时间复杂度O (N)相比效率有了质的提高。

待完善之处：指数暂支持输入整数。

思路

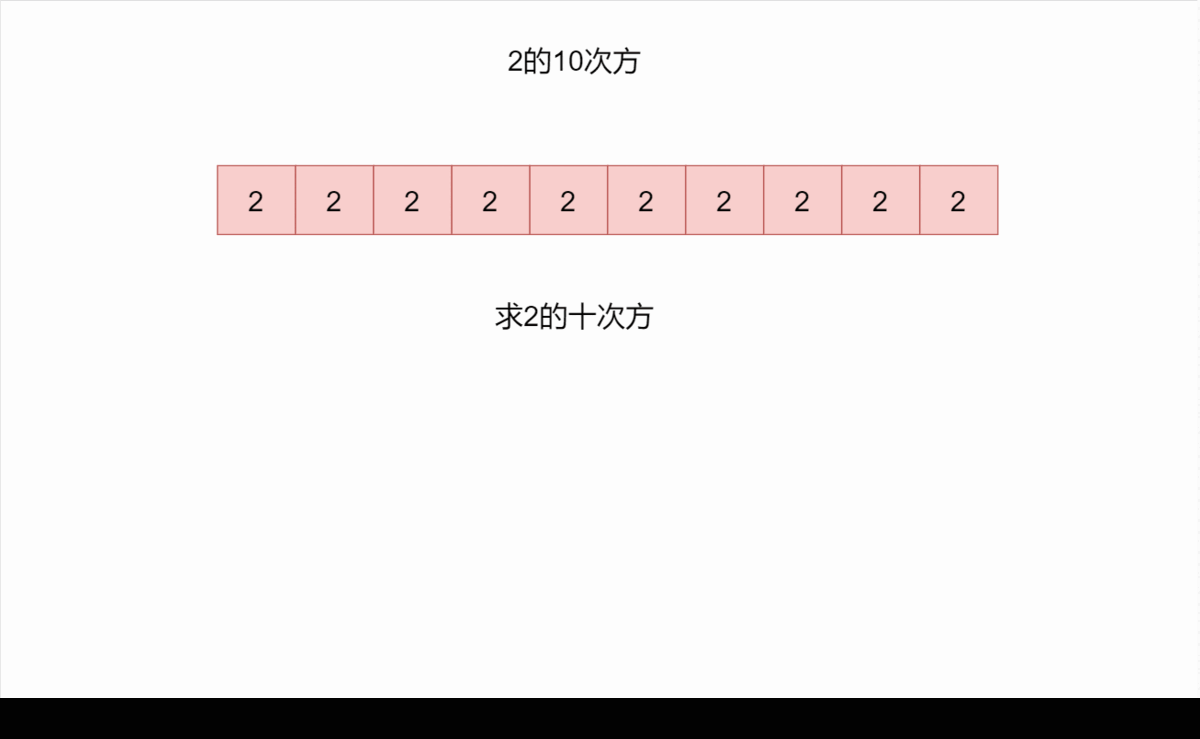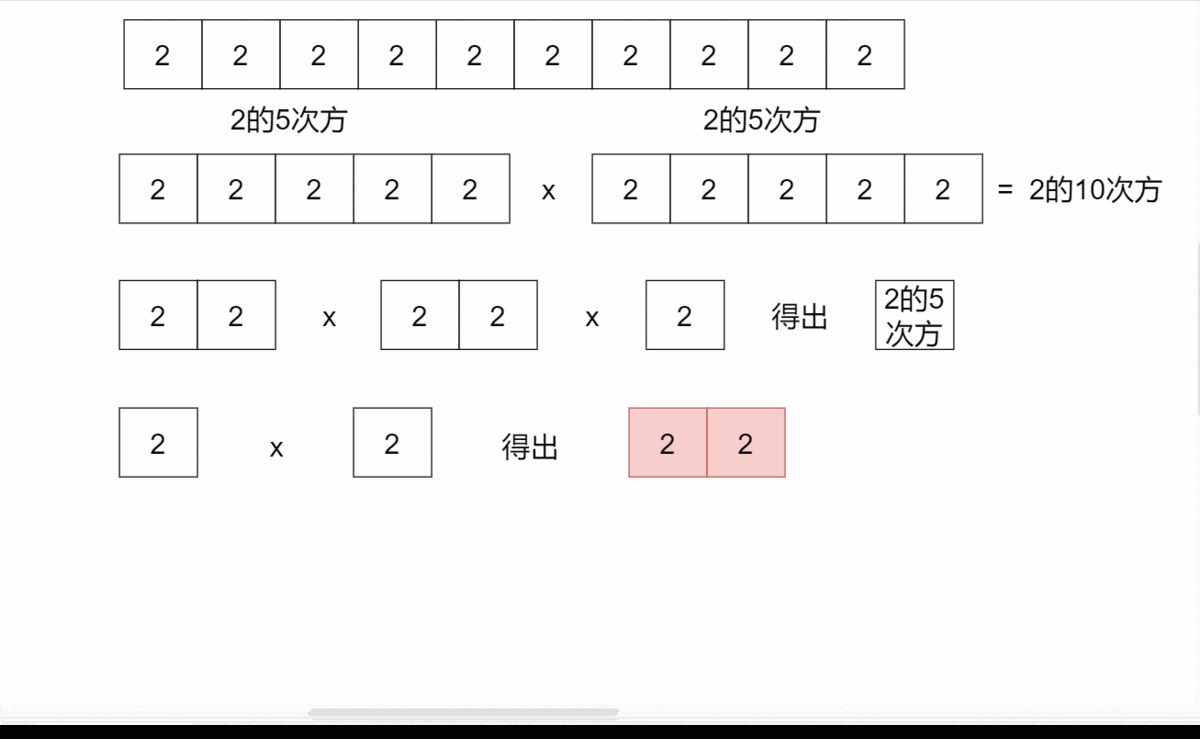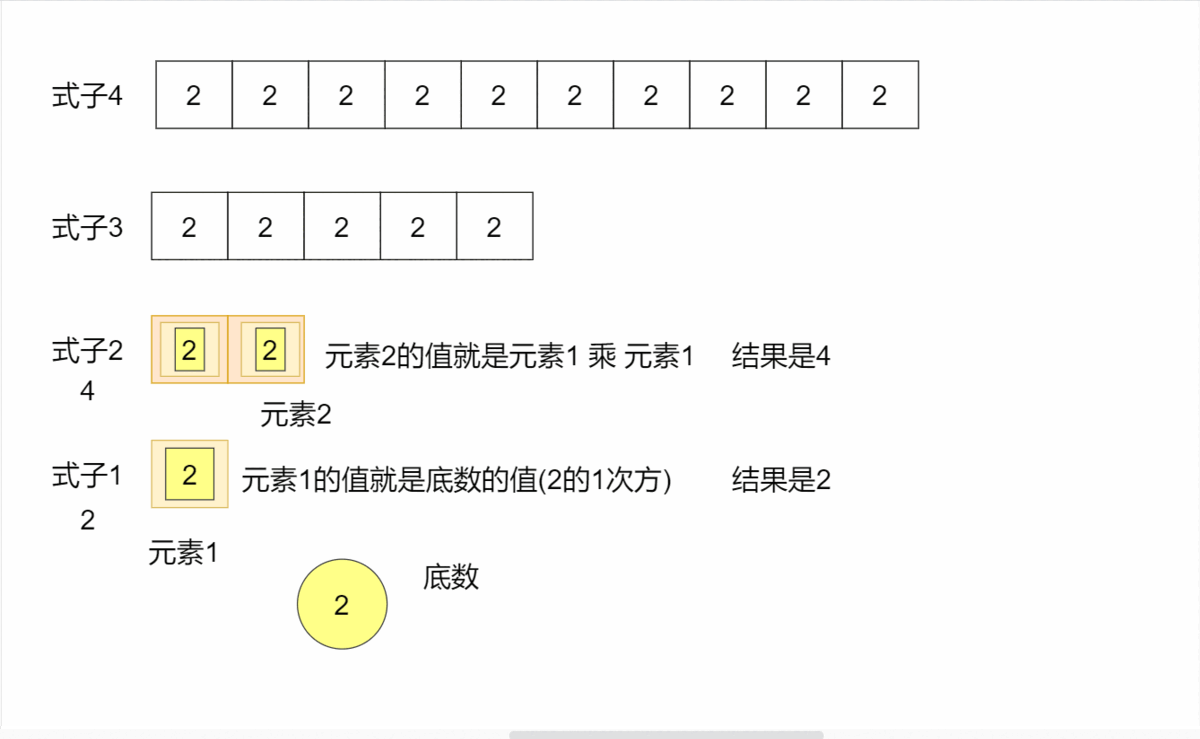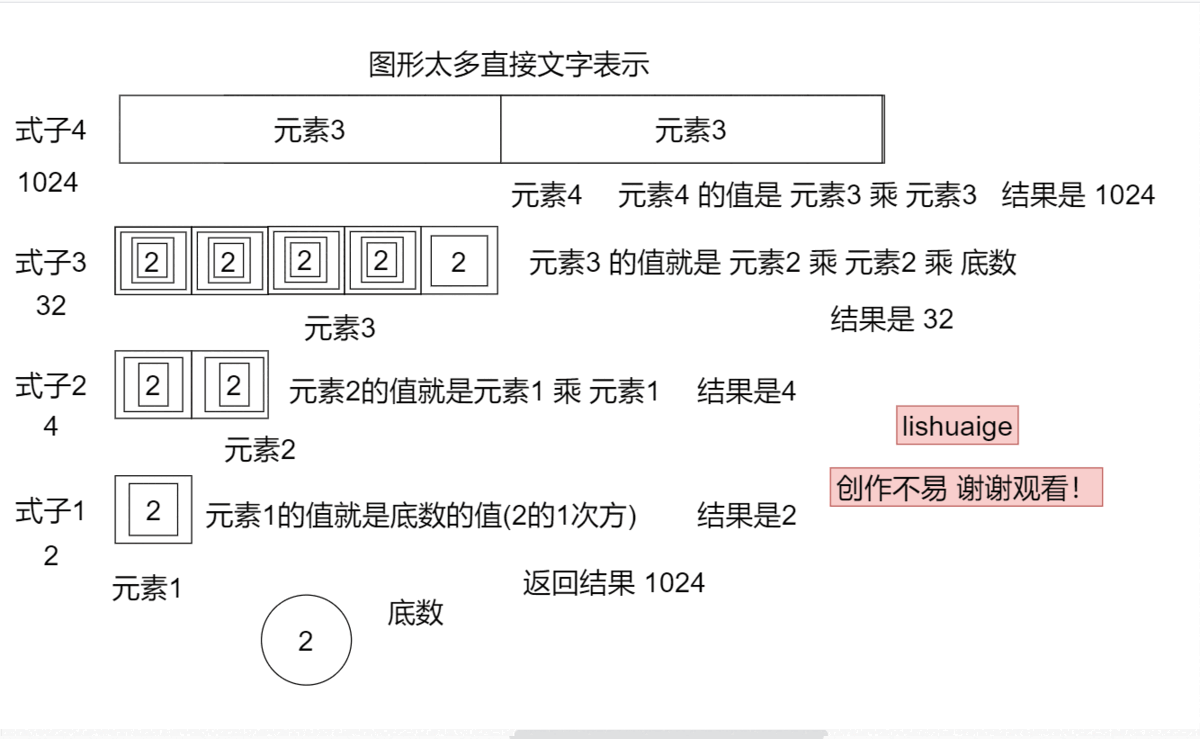
不断将高次幂拆分成低次幂，直到低次幂无法再拆分为止。而此时低次幂的值就显而易见了，就是底数（1次幂）。然后通过最低次幂（1次幂）不断往上求取更高次幂的值，最终得出结果。

我以2的10次方为例演示一实现思路。

解疑

1.拆分遵循的原则是什么？

每次将a的N次方拆分一半，拆分成 a的(N/2)次方 * a的(N/2)次方的形式。所以求a的N次方我们可以通过求出a的(N/2)次方得到。

但拆分需要考虑N的奇偶性。如果能完好拆分，就能通过a的(N/2)次方 * a的(N/2)次方计算a的N次方

否则只能通过a的(N/2)(向下取整)次方得出，另外还需要一个底数来补充，才能与a的N次方匹配。

特殊情况

• 当输入的指数为0时，无需进行递归，直接返回1。
• 当指数为负数时，求倒数，用1除以快速幂计算出来的结果

代码

class Solution:
    def myPow(self, x: float, n: int):

        # 快速幂运算
        def quickMul(N):
            if N == 1:
                # 返回底数
                return x
            # 得到拆分后的值 向下取整
            y = quickMul(N // 2)
            print(y)
            # 奇偶判断
            if N % 2 == 0:
                # 如果能完好拆分那么 a的N次方就是 a的(N/2)次方 * a的(N/2)次方
                return y * y
            else:
                # 否则还要还要多乘一个底数
                return y * y * x

        if n > 0:
            return quickMul(n)
        elif n == 0:
            return 1
        else:
            # 求倒数
            return 1.0 / quickMul(-n)


if __name__ == '__main__':
    print(Solution().myPow(2, 10))

吐槽

今天 ScreenToGif 导出不了gif，一直报错，折腾了我半天，最后找到一个线上转gif的，才勉强制作成功，真不容易呀..晚上房间灯又坏了，又折腾了好一会才换上新的，弄的今天写这个思路时断时续，现在好担心有啥表述不清晰或有误的地方，欢迎各位朋友批评指正！