如何判断两个平面相交_直线、平面平行的判定与性质

一、知识梳理

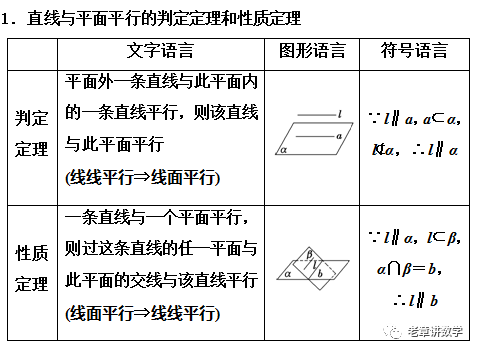
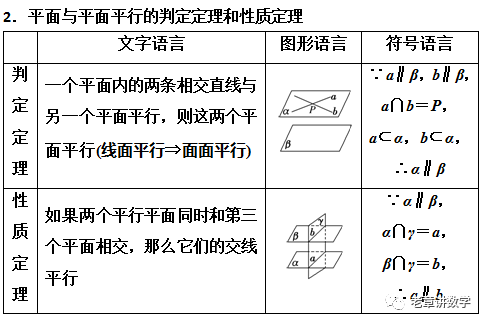
3.常用结论 (1)两个平面平行，其中一个平面内的任意一条直线平行于另一个平面． (2)如果一个平面内的两条相交直线分别平行于另一个平面内的两条相交直线，则这两个平面平行． (3)如果两个平面分别平行于第三个平面，那么这两个平面互相平行． (4)如果两个平面垂直于同一条直线，那么这两个平面互相平行． (5)夹在两个平行平面之间的平行线段长度相等． (6)两条直线被三个平行平面所截，截得的对应线段成比例． (7)同一条直线与两个平行平面所成角相等． (8)经过平面外一点有且只有一个平面与已知平面平行．二、典例精析

1.直线与直线、直线与平面平行的证明

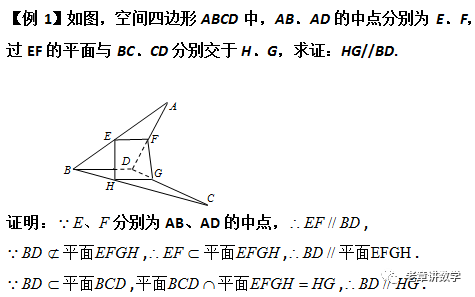
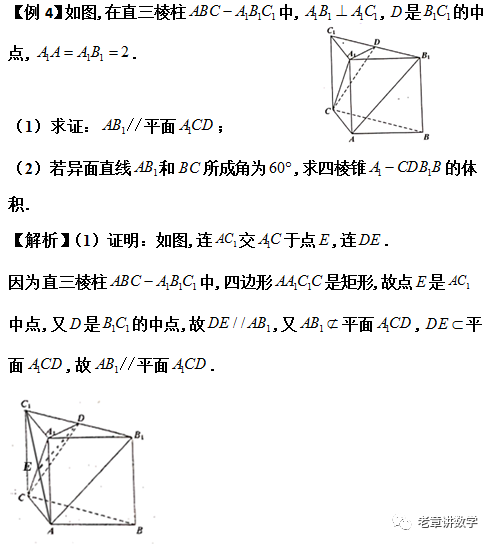
方法提炼 1. 判断或证明线线平行的常用方法 (1) 利用三角形、梯形中位线性质：三角形(或梯形)的中位线平行于底边； (2) 利用“如果一条直线截三角形的两边 ( 或两边的延长线 ) 所得的对应线段成比例，那么这条直线平行于三角形的第三边”； (3) 利用平行四边形的性质：平行四边形的对边平行； (4) 利用线面平行的性质定理： 一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行； (5) 利用面面平行的性质定理： 如果两个平行平面同时和第三个平面相交，那么它们的交线平行； (6) 利用平行的传递性，即公理 4 ：若 a //b,b//c ，则 a //c. (7) 利用线面垂直的性质：若两条直线垂直于同一个平面，则这两条直线平行 . 2. 判断或证明线面平行的常用方法 (1) 利用线面平行的定义 ( 无公共点 ) ，一般用反证法 ; (2) 利用线面平行的判定定理 : 平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行 ; (3) 利用面面平行的性质 : 两个平面平行，其中一个平面内的任意一条直线平行于另一个平面 .2. 面面平行的证明

方法提炼 判断或证明面面平行的常用方法 (1) 面面平行的定义，即证两个平面没有公共点 ( 不常用 ), 常用反证法完成证明 ； (2) 面面平行的判定定理：如果一个平面内有两条相交直线都平行于另一个平面，那么这两个平面平行 ( 主要方法 ) ； (3) 如果一个平面内的两条相交直线分别平行于另一个平面内的两条直线，则这两个平面平行 ( 要先由 “ 线线平行 ” 推出“ 线面平行 ” 再到“ 面面平行 ” ，在证明题中不能直接由“ 线线平行 ” 得出“ 面面平行 ”) ； (4) 利用垂直于同一条直线的两个平面平行 ( 客观题常用 ) ； (5) 如果两个平面同时平行于第三个平面，那么这两个平面平行 ( 客观题常用 ) .3. 平行关系的综合应用

方法提炼 利用线面平行或面面平行的性质，可以实现与线线平行的转化，尤其在截面图的画法中，常用来确定交线的位置．对于线段长或线段比例问题，常用平行线对应线段成比例或相似三角形来解决．4. 平行关系中的探究性问题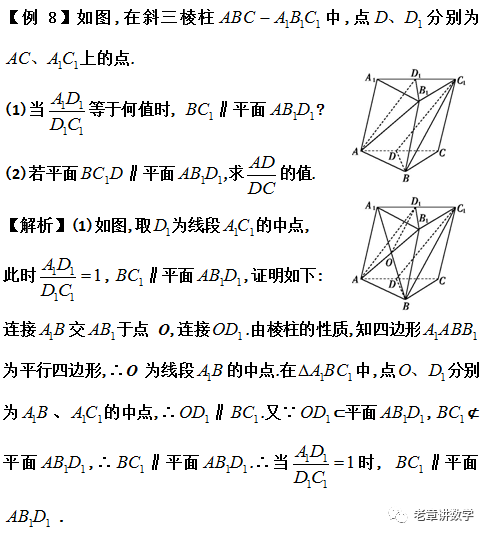

方法提炼 解决探究性问题一般先假设求解的结果存在 , 从这个结果出发 , 寻找使这个结论成立的充分条件 , 如果找到了使结论成立的充分条件 , 则存在 ; 如果找不到使结论成立的充分条件 ( 出现矛盾 ), 则不存在 . 而对于探求点的问题 , 一般是先探求点的位置 , 多为线段的中点或某个三等分点 , 然后给出符合要求的证明 .三、题组训练

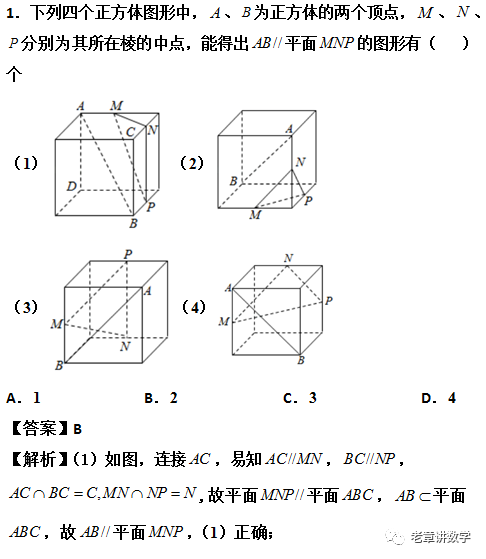
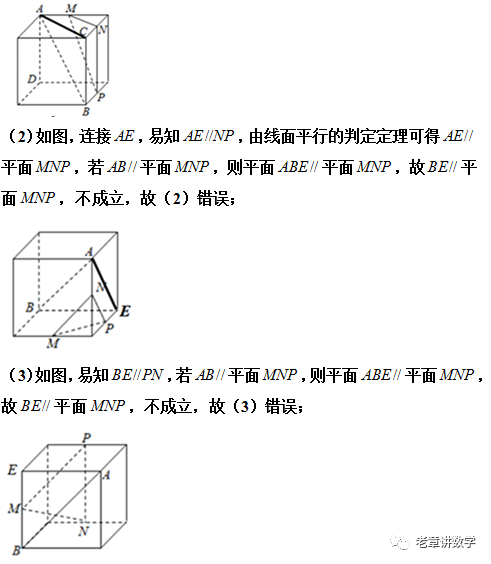
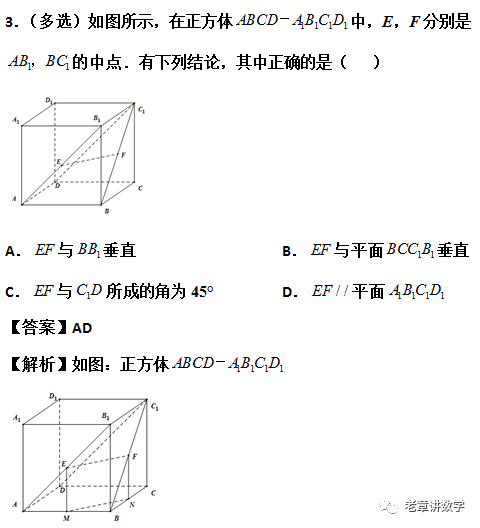
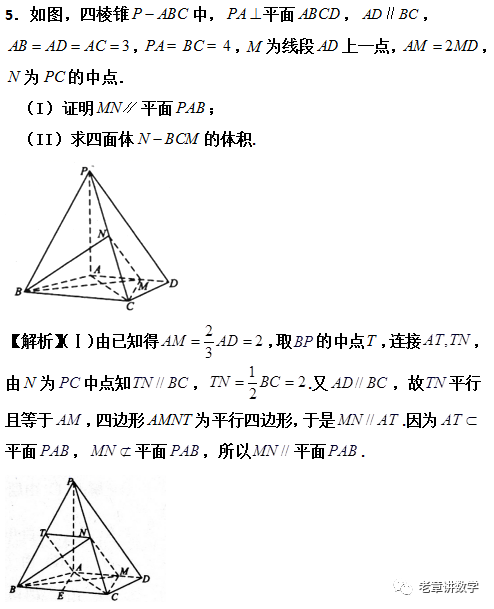
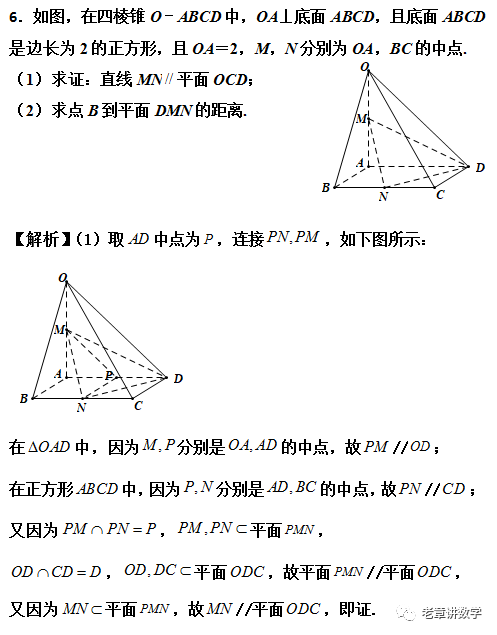
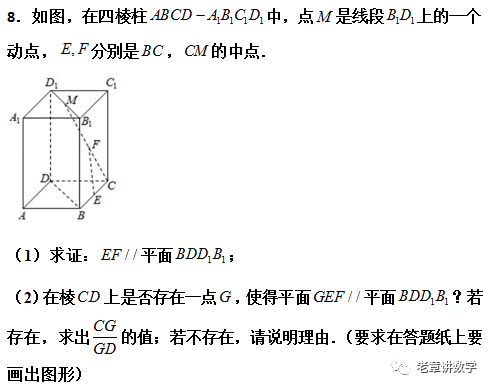
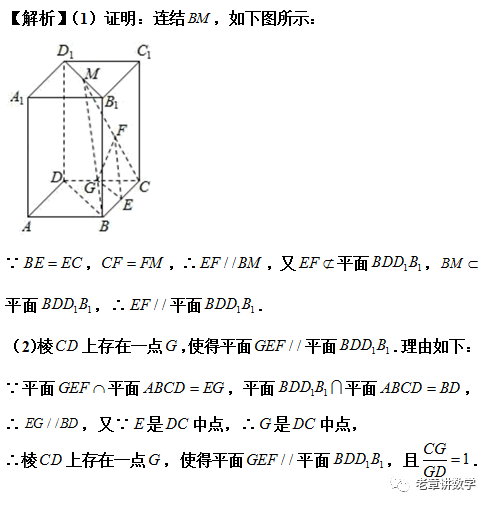
数学世界这么大  扫我带你去看看

↓↓↓ 点击"阅读原文" 【查看更多信息】