1.最小生成树

生成树：所有顶点均由边连接在一起，但不存在回路的图。

一个图可以有许多棵不同的生成树。

所有生成树具有以下共同特点：

生成树的顶点个数与图的顶点个数相同；

生成树是图的极小连通子图，去掉一条边则非连通；

一个有n个顶点的连通图的生成树有n-1条边；

在生成树中再加一条边必然形成回路；

生成树中任意两顶点间的路径是唯一的；

含n个顶点n-1条边的图不一定是生成树。

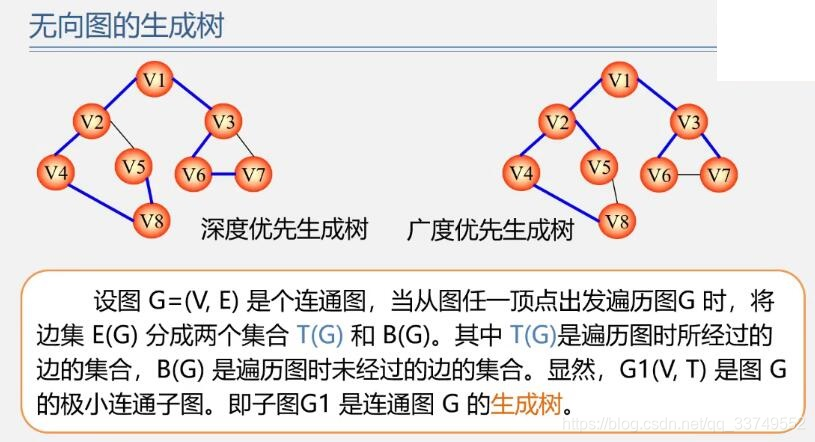
无向图的生成树

深度优先生成树

广度优先生成树

最小生成树：给定一个无向网络，在该网的所有生成树中，使得各边权值之和最小的那棵生成树称为该网的最小生成树，也叫最小代价生成树

构造最小生成树（MST）

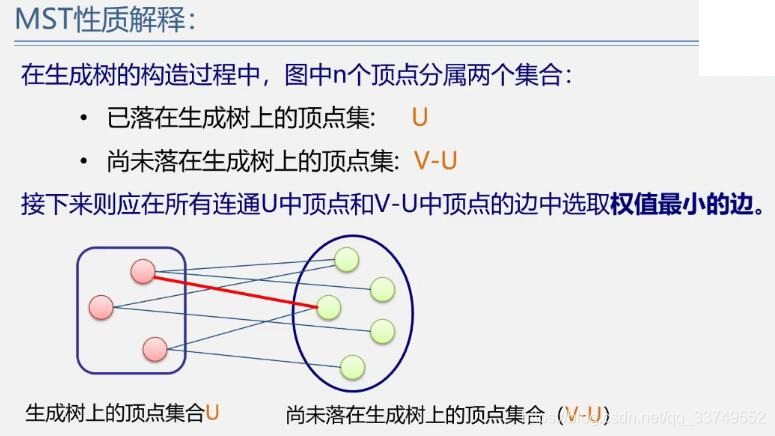
MST性质解释：

构造最小生成树方法一：普里姆（Prim）算法

指定一个点，选择与该点连接的权值最小的点，选择到的点再次选择与该点连接的权值最小的点

构造最小生成树方法二：克鲁斯卡尔（Kruskal）算法

循环查找权值最小的边

最小生成树可能不唯一

两种算法比较

2.最短路径

典型用途：交通网络的问题--两地之间的最短路径

问题抽象：在有向网中A点（源点）到达B点（终点）的多条路径中，寻找一条各边权值之和最小的路径，即最短路径。

最短路径与最小生成树不同，路径不一定包含n个顶点，也不一定包含n-1条边。

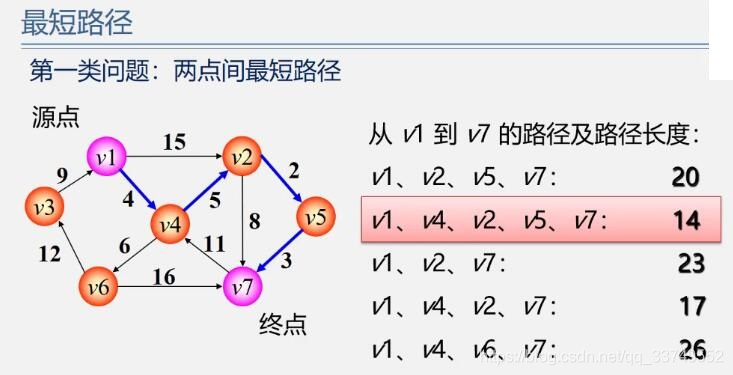
第一类问题：两点间最短路径

第二类问题：某源点到其他各点最短路径

两种常见的最短路径问题：

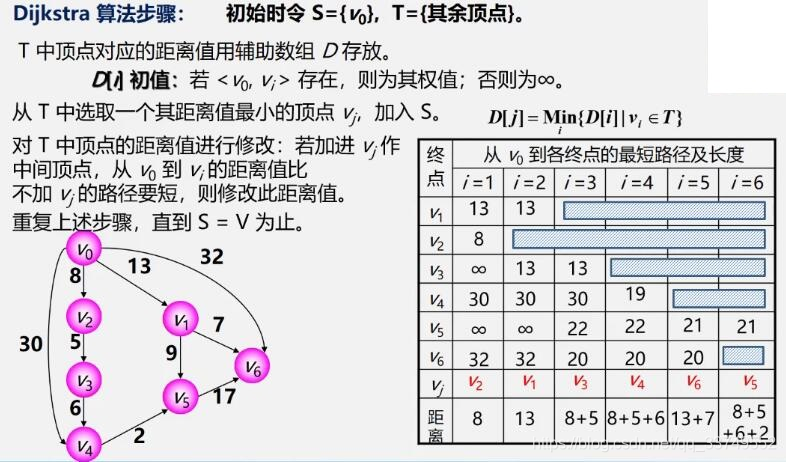
一、单源最短路径用Dijkstra（迪杰斯特拉）算法

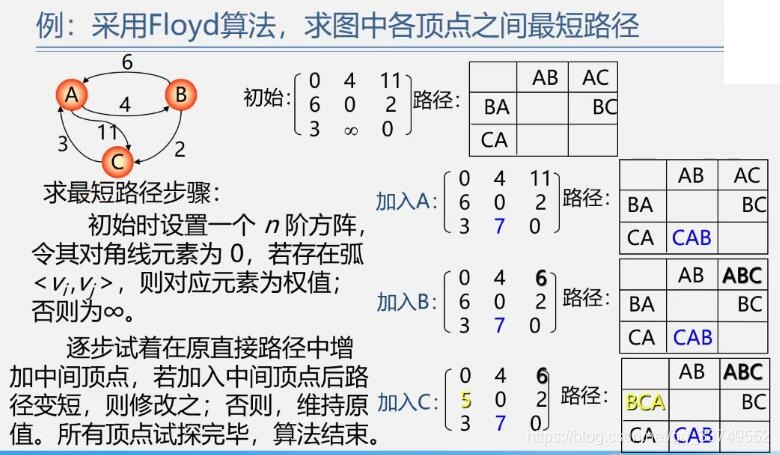
二、所有顶点间的最短路径用Floyd（弗洛伊德）算法

Dijkstra（迪杰斯特拉）算法  时间复杂度O(n2)

指定一个源点，分别计算到其他点的路径长度，选取最小的一个，然后用着两个点，再去找第三个点....

所有顶点间的最短路径

方法一：每次以一个顶点为源点，重复执行Dijkstra算法n次。 时间复杂度O(n3)

方法二：Floyd（弗洛伊德）算法 时间复杂度O(n3)

先用二位数组算各个路径的长度，加入一个点，从第一个点开始加，只算一个点，利用这个点，再算到其他点的路径长度，知道把所有的点都加上

算法思想：

逐个顶点试探

从vi到vj的所有可能存在的路径中

选出一条长度最短的路径

3.拓扑排序

有向无环图及其应用

有向无环图：无环的有向图，简称DAG图

AOV网：（解决拓扑排序问题）

用一个有向图表示一个工程的各个子工程及其相互制约的关系，其中以顶点表示活动，弧表示活动之间的优先制约关系，称这种有向图为顶点表示活动的网，简称AOV网

AOE网：（解决关键路径问题）

用一个有向图表示一个工程的各个子工程及其相互制约的关系，其中以弧表示活动，顶点表示活动的开始或结束事件，称这种有向图为边表示活动的网，简称AOE网

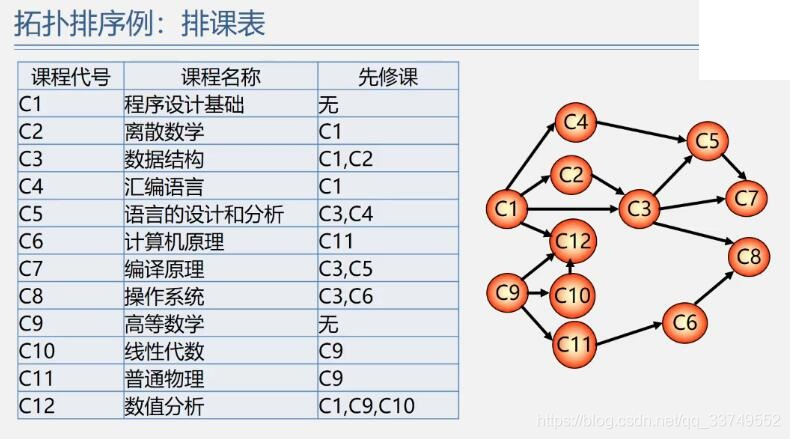
拓扑排序例子：排课表

AOV网特点：

若从i到j有一条有向路径，则i是j的前驱，j是i的后继。

若<i,j>是网中有向边，则i是j的直接前驱，j是i的直接后继。

AOV网中不允许有回路，因为如果有回路存在，则表明某项活动以自己为先决条件，显然这是荒谬的。

问题：如何判断AOV网中是否有回路

拓扑排序：

在AOV网中没有回路的前提下，我们将全部活动排列成一个线性序列，使得若AOV网中有弧<i,j>存在，则在这个序列中，i一定排列在j的前面，具有这种性质的线性序列称为拓扑有序排列，相应的拓扑有序排列的算法称为拓扑排序。

拓扑排序的方法：

1.在有向图中选一个没有前驱的顶点输出。

2.在图中删除该顶点和所有以它为尾的弧。

3.重复上述两个步骤，直至全部顶点均已输出；或者当图中不存在无前驱的顶点为止。

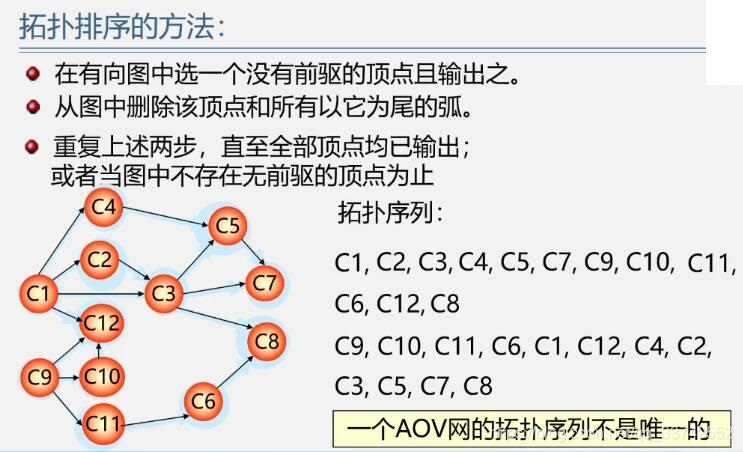
一个AOV网的拓扑序列不是唯一的

在图中存在i->j的一条边，拓扑序列一定是先输出i，在输出j

检测AOV网中是否存在环的方法：对有向图构造其顶点的拓扑有序序列，若网中所有顶点都在它的拓扑有序序列中，则该AOV网必定不存在环。

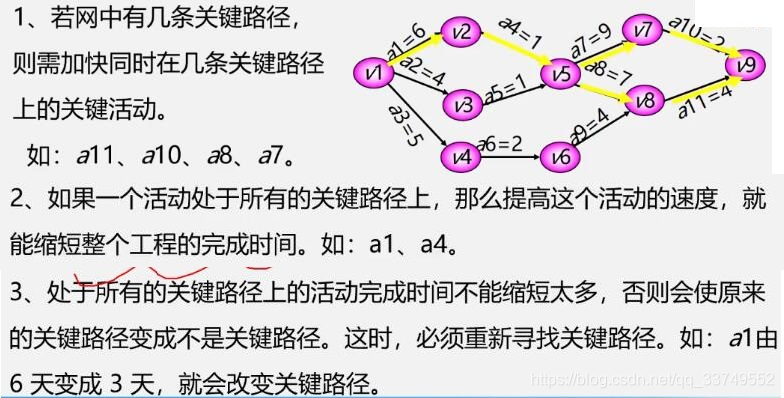
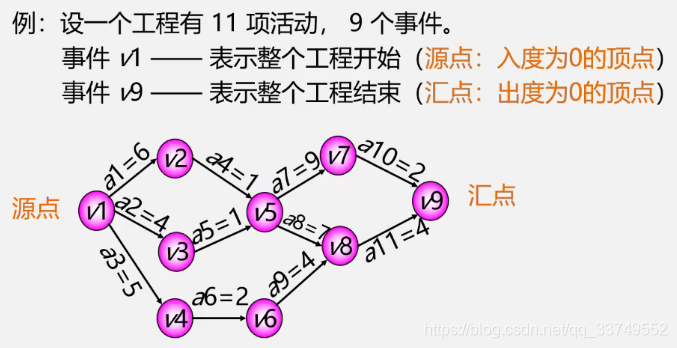
4.关键路径

把工程计划表示为边表示活动的网络，即AOE网，用顶点表示事件，弧表示活动，弧的权表示活动持续时间。

事件表示在它之前的活动已经完成，在它之后的活动可以开始。

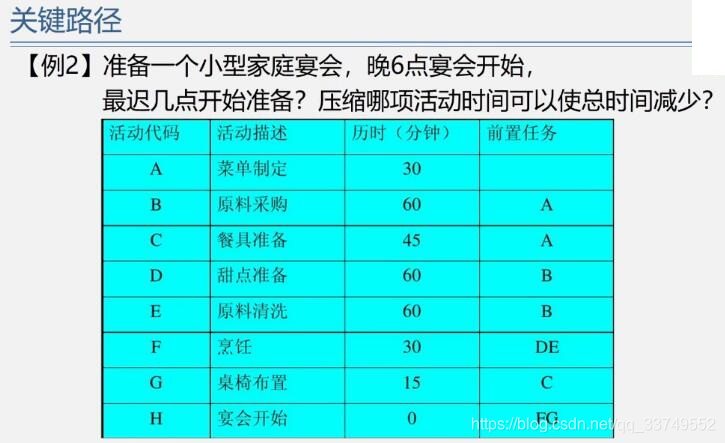
关键路径——路径长度最长的路径

路径长度——路径上个活动持续时间之和

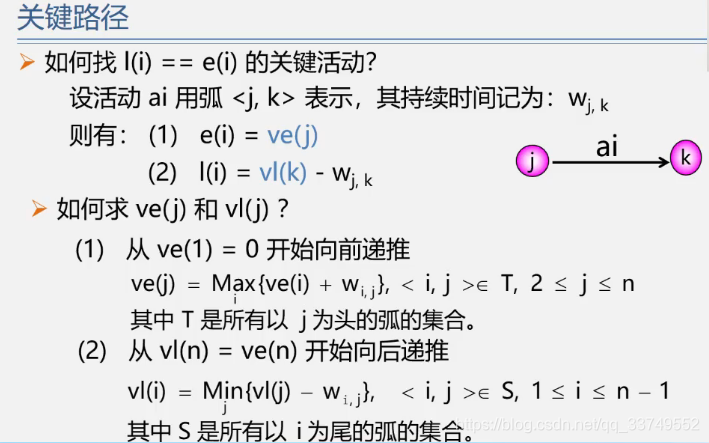
最早发生时间是指向这个结点之前的路径的最大值，要等第一层盖完了，再去盖第二层，从前往后算

最晚发生时间是指最长可以拖多长时间，从后往前算

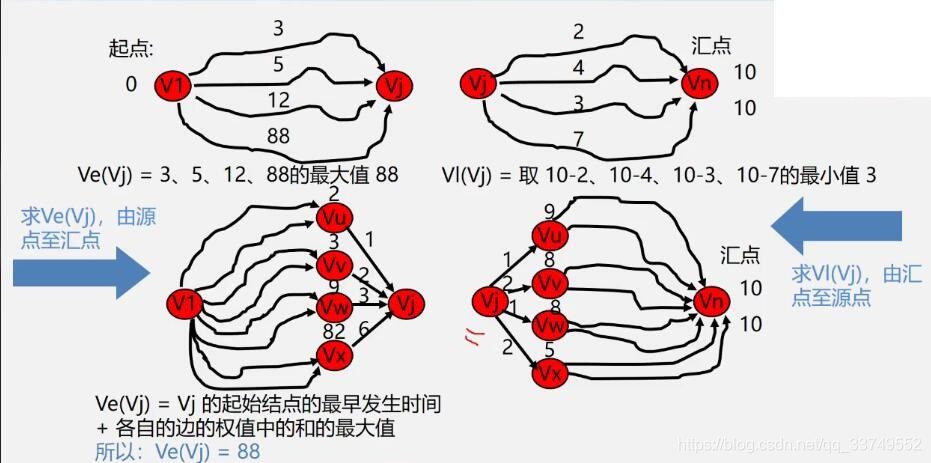
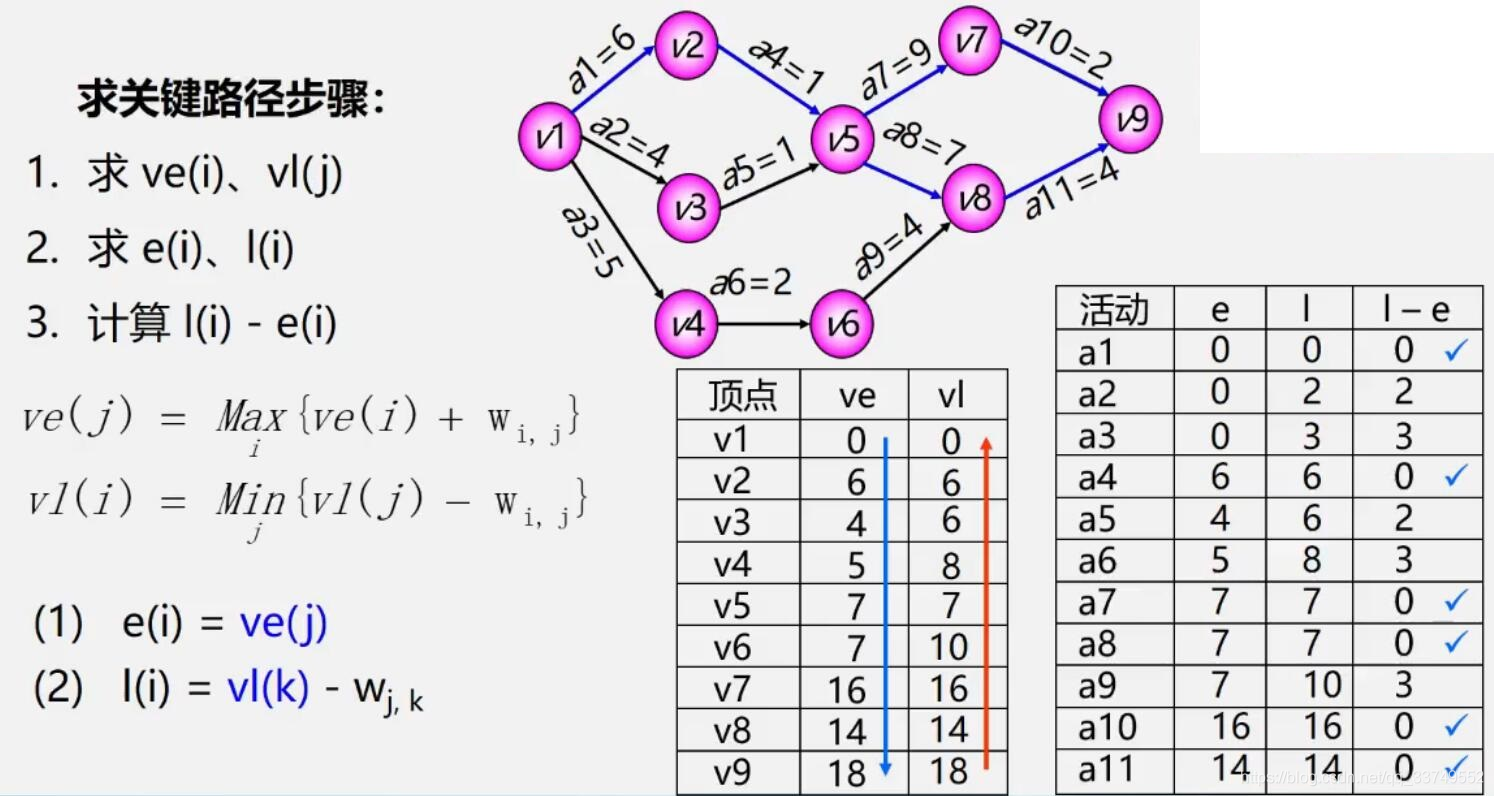
关键路径的讨论