函数的定义域是我们上了高中后接触到的新的名词,其实相关知识我们早有接触,其实它就是我们之前学习函数中自变量x的取值范围,到了高中我们将这个取值范围定义为函数的定义域。
那如何理解定义域呢?数学总是抽象难理解的,函数更上如此,所以相当一部分同学听到函数就头皮发麻。
所以为了了解抽象的定义域我先从具体的事例开始说明。比如人类的活动区域可以视为一个定义域,具体指地球上的陆地部分(有人会觉得我们有时候会去水里游泳呀,等等不一定一直在陆地,emmm我要讲的一个意思是人类是陆生动物,日常生活都在陆地上进行,如果长时间待在水里将死亡),那么鸟类活动区域的定义域就是陆地与天空,相比与人类它的定义域更大....
还比如,如果将饮食的种类视为一个定义域,人类的这个定义域包括鸡鸭鱼肉五谷杂粮等等等等,但是肉食动物的饮食定义域只包括肉类,草食动物的饮食定义域只包括一些植物。
.....
我们回归书本上的函数继续讲。我先拿两个我们最常接触的函数做一个对比。
1、一次函数y=x
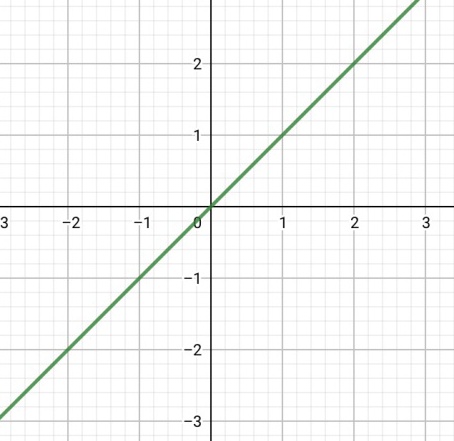
2、反比例函数y=1/x
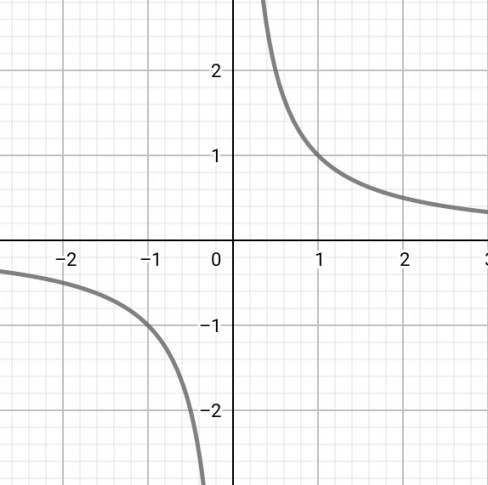
那么他们两个函数的定义域可视为x可以到达的区域(类比与人类的活动区域,或饮食种类),又一次函数中x可以到达x轴上的任意一个位置也就是说它可以取x轴上的任何一个数字,所以我们规定一次函数的定义域为R,但是反比例函数中x不能到达x=0处(类比人类不能生活在水里),所以反比例函数的定义域就是(-∞,0)∪(0,+∞).
接着讲解在高中阶段我们所接触的函数的定义域:
1、幂函数
(1)一次函数,定义域为R.
(2)二次函数,定义域为R
(3)反比例函数,定义域为(-∞,0)∪(0,+∞).
前面三个函数图像过于简单,不再展示。
(4)偶次根式函数,定义域为[0,+∞)
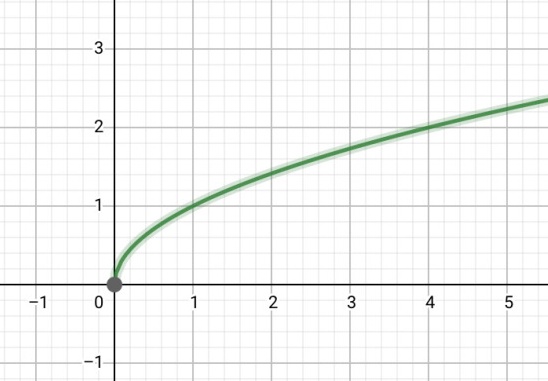
(5)y=x°,定义域为{x|x≠0}
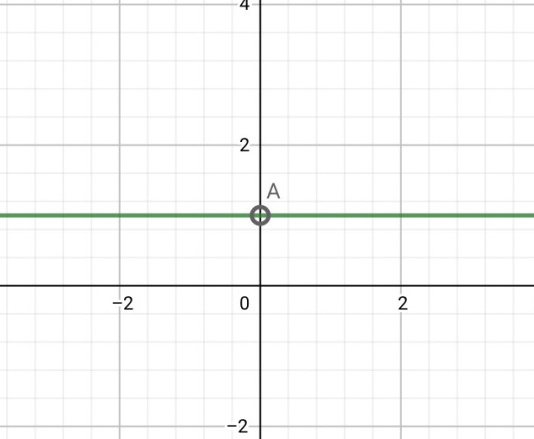
2、指数函数,定义域为R
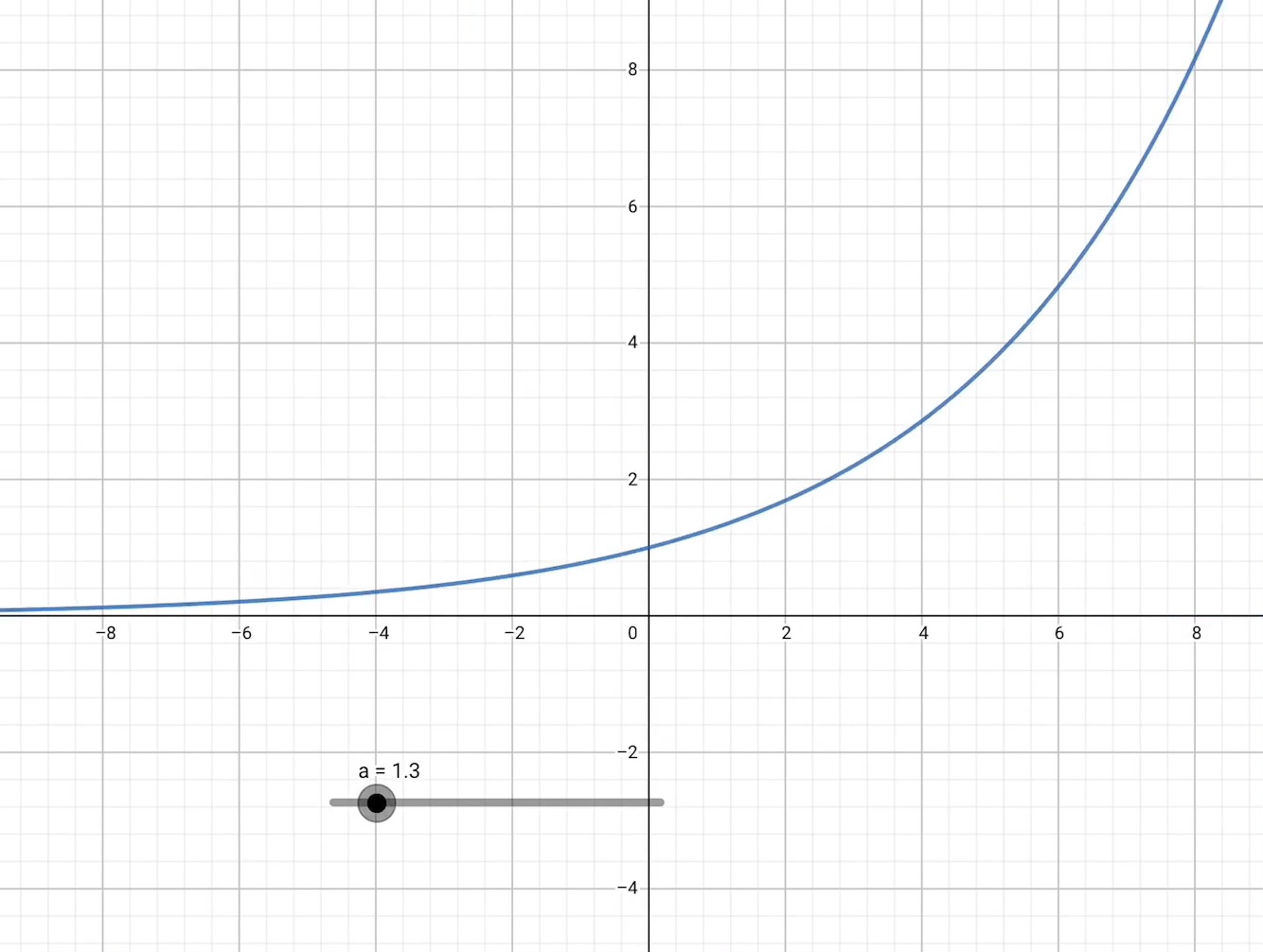
3、对数函数,定义域为(0,+∞)
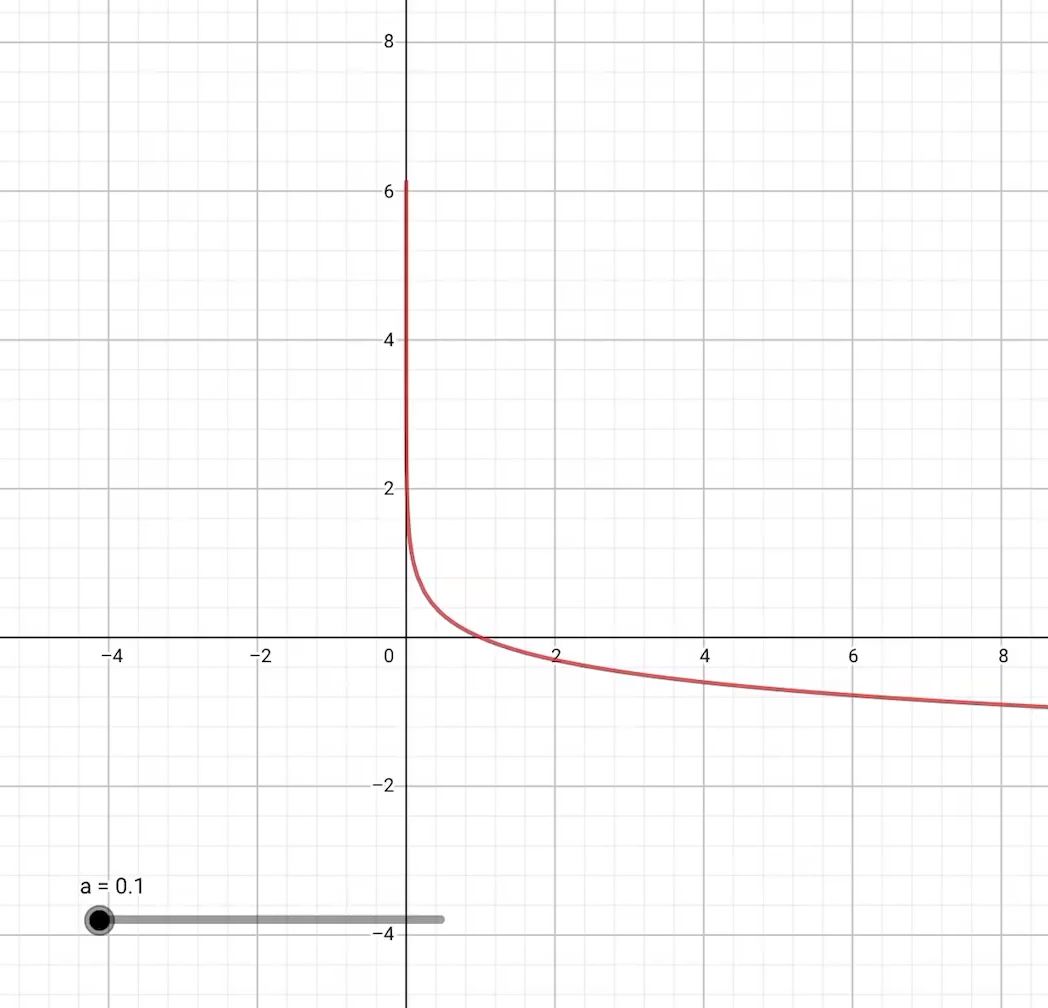
4、三角函数y=sinx与y=cosx定义域都为R
重点是y=tanx定义域为{x|x≠kπ+2/π}所有函数y=tanx的图像存在渐近线.
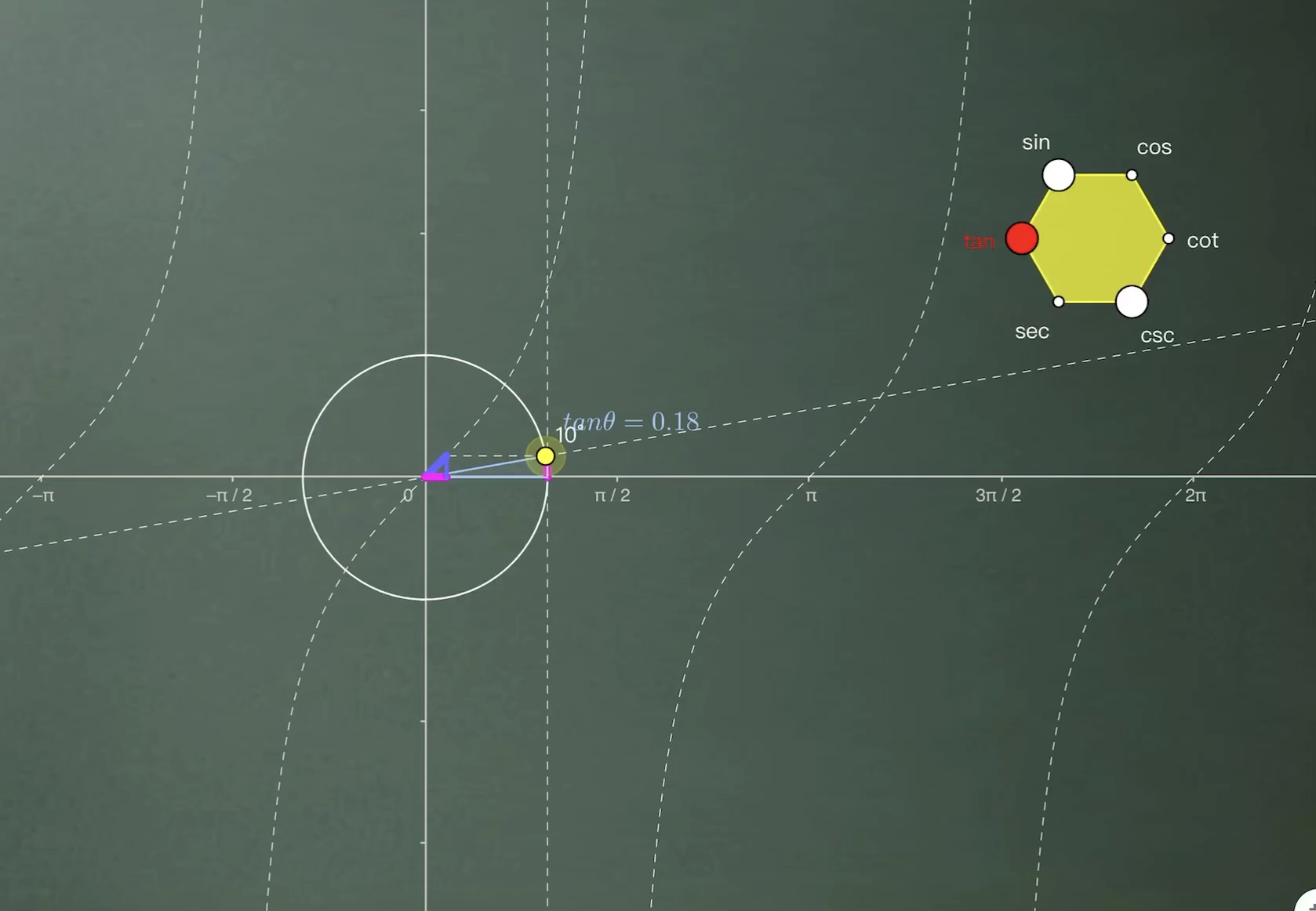
而高中考察定义域最主要的内容是复合函数定义域的求解,前提是掌握好以上几类函数的定义域的具体情况,才能更好的解决复合函数问题。