蜂房结构、火箭的最佳发射时间、人造卫星的最佳工作状态;节约下料、物资调度、仓库存储、投资组合、金融策略、优选试验,精益求精是自然进化、人类发展的一个永恒话题。
最优化,人类智慧的结晶。田忌赛马、华罗废的优选法、线性规划…"多、快、好、省"是生产实践的"最优化"要求,最优化理论构成了20世纪数学发展的一个亮点
康托罗维奇(1912-1986),苏联经济家,1938年首次提出求解线性规划问题的方法,曾获得1975年的诺贝尔经济学奖。线性规划是帮助人们进行科学管理的一种数学方法,研究线性约束条件下线性目标函数极值的数学理论和方法。
若图形甲的顶点均在图形乙的边界上,则称图形甲为图形乙的内接图形,它包含以下基本形式:三角形内接三角形、三角形内接四边形、四边形内接三角形、圆内接三角形、圈内接四边形等。
转化与化归是一种重要的数学思想,在数学学习与解数学题中,我们常常用到下列不同途径的转化:实际问题转化为数学问题,数与形的转化,常量与变量的转化,一般与特殊的转化等。

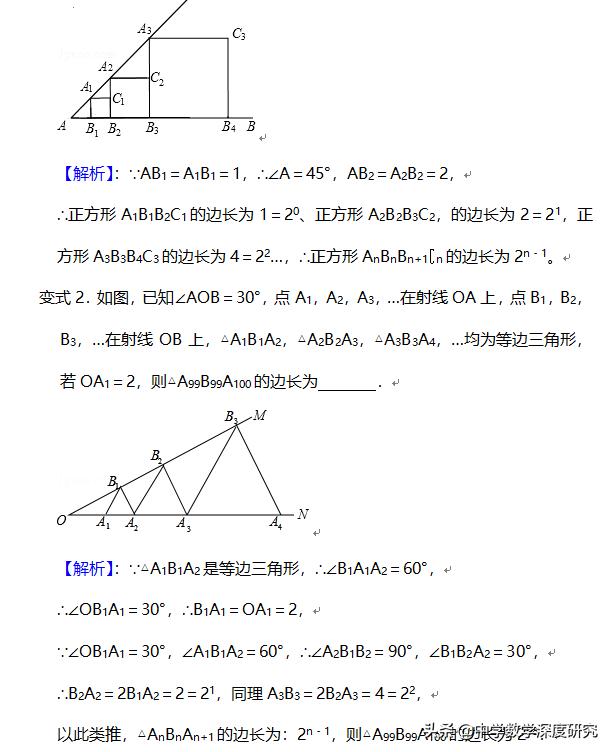

例2.某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:
定义:如果一个正方形的四个顶点都在一个三角形的边上,那么我们就把这个正方形叫做三角形的内接正方形.
结论:在探讨过程中,有三位同学得出如下结果:
甲同学:在钝角、直角、不等边锐角三角形中分别存在____个、____个、_____个大小不同的内接正方形.
乙同学:在直角三角形中,两个顶点都在斜边上的内接正方形的面积较大.
丙同学:在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.
任务:(1)填充甲同学结论中的数据;
(2)乙同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;
(3)请你结合(2)的判定,推测丙同学的结论是否正确,并证明.
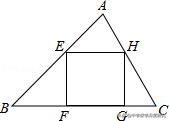
【解析】:(1)1,2,3.
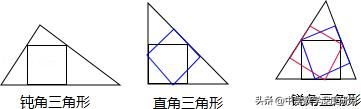
(2)乙同学的结果不正确.
例如:在Rt△ABC中,∠B=90°,AB=BC=1,则AC=√2.
如图①,四边形DEFB是只有一个顶点在斜边上的内接正方形.

∴在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.
变式1.如图Rt△ABC中有两种作内接正方形的方法.图(1)作的内接正方形面积为441,(2)中作的内接正方形的面积为440,则AC+BC的值为( )
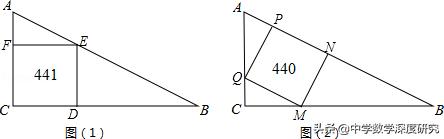
A.456 B.458 C.460 D.462
【解析】:如图,设BC=a,AC=b,AB=c.
在图(1)中,∵四边形EFCD是正方形,
∴EF∥BC,∴Rt△AFE∽Rt△ACB,
∴EF:BC=AF:AC,21:a=(b﹣21):b,


例3.如果一个矩形的四个顶点分别在三角形的各条边上,那么就称这个矩形为此三角形的内矩形如图1,矩形DEFG是△ABC的内接矩形,学习了三角形的内接矩形后,小明对此产生了浓厚的兴趣,并做了以下探索与猜想.
(一)探究与发现:
已知:如图2,在Rt△ABC中,∠ACB=90°,AC=3,BC=4.小明利用位似图形的方法,做出Rt△ABC的内接正方形CDEF,请你参照小明的方法,在图3中画出Rt△ABC的内接正方形,使正方形的一边落在AB边上,其余两个顶点分别在BC、AC上.(不写画法,保留画法,保留画图痕迹,画图工具不限)
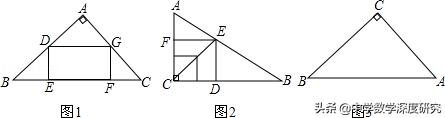
(2)请问图3中的内接正方形的面积是该三角形内接矩形的最大面积吗?_____(填"是"或"不是"),若不是,则该三角形内接矩形的最大面积是______.
(3)经过探究小明发现并证明了直角三角形的内接矩形一定存在最大面积,且内接矩形的最大面积与直角三角形面积的比是_____-.
(二)猜想与说理:
小明猜想:在Rt△ABC中,若∠ACB=90°,AB=c,斜边AB上的高为h,(其中c,h为常数)则该三角形的内接矩形的对角线一定存在最小值.小明的猜想正确吗?若正确,请你求出三角形内接矩形对角线的最小值、若不正确,请说明理由.
【解析】:(一)(1)如图3所示,正方形EFGH即为所求作.
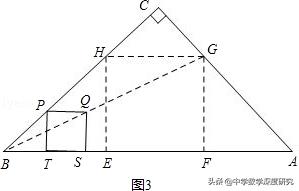
(2)①若矩形EFGH是正方形,
过点C作CN⊥AB于N,交GH于M,则CM⊥GH.如图4,
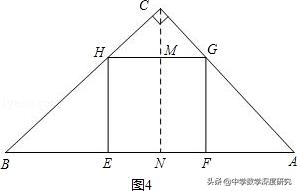
设正方形EFGH的边长为x,则有GH=EH=MN=x.
∵∠ACB=90°,AC=3,BC=4,

②若矩形EFGH不是正方形,
过点C作CN⊥AB于N,交GH于M,则CM⊥GH.如图5,
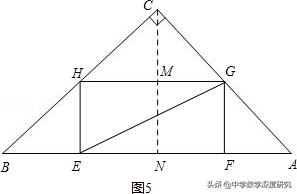

∴内接正方形的面积不是最大,该三角形内接矩形的最大面积是3.
故答案分别为:不是、3;
(3)∵内接矩形的最大面积为3,直角三角形面积为1/2×4×3=6,
∴内接矩形的最大面积与直角三角形面积的比是1/2.
故答案为:1/2;
(二)小明的猜想正确.如图5,
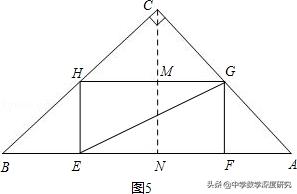
∵四边形EFGH是矩形,∴GH∥EF,∴△CGH∽△CAB.

本题主要考查了位似变换、相似三角形的判定、相似三角形的性质(相似三角形的对应高的比等于相似比)、二次函数的最值性、勾股定理等知识,在解决问题的过程中,用到了重要的数学方法﹣配方法,求多项式的最值,常常可通过运用配方法来解决问题.
变式1.阅读以下内容并回答问题:
如图1,在平面直角坐标系xOy中,有一个△OEF,要求在△OEF内作一个内接正方形ABCD,使正方形A,B两个顶点在△OEF的OE边上,另两个顶点C,D分别在EF和OF两条边上.
小丽感到要使四边形的四个顶点同时满足上述条件有些困难,但可以先让四边形的三个顶点满足条件,于是她先画了一个有三个顶点在三角形边上的正方形(如图2).接着她又在△OEF内画了一个这样的正方形(如图3).她发现如果再多画一些这样的正方形,就能发现这些点C位置的排列图形,根据这个图形就能画出满足条件的正方形了.
(1)请你也实验一下,再多画几个这样的正方形,猜想小丽发现这些点C排列的图形是_____;
(2)请你参考上述思路,继续解决问题:如果E,F两点的坐标分别为E(6,0),F(4,3).
①当A₁的坐标是(1,0)时,则C1的坐标是______ ;
②当A₂的坐标是(2,0)时,则C2的坐标是______;
③结合(1)中猜想,求出正方形ABCD的顶点D的坐标,在图3中画出满足条件的正方形ABCD.
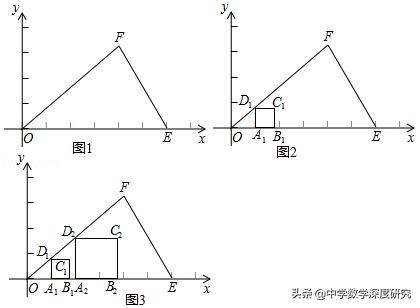
【解析】:(1)一条线段;
(2)∵F(4,3).∴直线OF的表达式是y=3/4x,

所以直线EF的表达式为y=﹣3/2x+9
直线EF:y=﹣3/2x+9与直线C1C2:y=3/7x的交点坐标为C.
解得x=14/3,y=2.∴C点坐标为(14/3,2).
把y=2代入y=3/4x,解得x=8/3,∴D点坐标为(8/3,2)
即:所画四边形ABCD如图3所示,



求解与图形内接相关最值的问题的常用基本方法有:
(1)特殊位置与极端位置法:先考虑特殊位置或极端位置,确定最值的具体数据,再进行一般情形下的推证;
(2)几何定理(公理)法:应用几何中的不等量性质、定理;
(3)数形结合法:揭示问题中变动元素的代数关系,构造二次函数等。