以下是随意找出的4组不同的测试数据,这里只讨论被除数与除数符号不同的情况。
结果均是由java代码实现。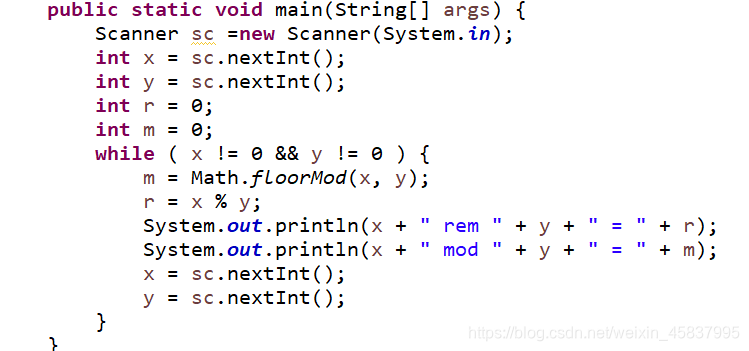
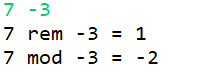
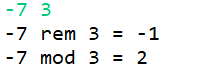
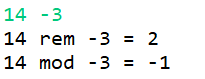
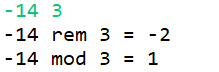
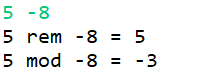

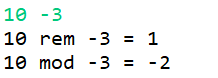
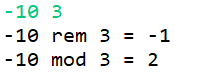
*
横行的规律:
当被除数与除数符号交换时,其取余运算结果和取模运算结果也随之交换。
竖列的规律:
不难发现:取余运算结果的符号总是与被除数保持一致,而取模运算的结果总是与除数保持一致。
推导:
先来看看定义是怎么说的:
定义
给定一个正整数p,任意一个整数n,一定存在等式 :
n = kp + r ;
其中 k、r 是整数,且 0 ≤ r < p,则称 k 为 n 除以 p 的商,r 为 n 除以 p 的余数。
对于正整数 p 和整数 a,b,定义如下运算:
取模运算:a % p(或a mod p),表示a除以p的余数。
这里的定义只给出了除数为正整数的情况,不足以来说明情况,不妨将定义推广到负数的范围,即
给定两个整数a,b,且b非零,那么一定存在两个整数c,r(0 <= |r| < |b| ) 使:a = c * b + r;
所以:对于整型数a,b来说,取模运算或者求余运算的方法都是:
1.求整数商: c = a / b;
2.计算模或者余数: r = a - c * b.
由此可见:商c的符号只有a、b有关,并且,造成取模运算和取余运算结果不同的原因在于第一步求商时,c的取值方法不同:
取余运算在求商时,总倾向于向 0 方向舍入(相当于fix()函数 ),即总趋向于使商的绝对值变得更小。
取模运算在求商时,总倾向于向 负无穷 方向舍入 (相当于floor()函数),即总趋向于使商的绝对值变得更大。
因此:当c为正数,也就是当a和b同号的时候,向0取整和像负无穷取证的作用是相同的,此时取余运算和取模运算
没有
区别。
当a、b异号时,c(取余运算所得商) >= c(取模运算所得商),从而造成了二者第二步时求余数的运算结果的不同。
余数的符号判断
余数r的符号是由 a 和 c * b 所决定的,当 a > 0 ,b < 0 时,此时 c < 0 ,c * b > 0由第2步可知:r的正负由a 与c * b的大小所决定,我们已经知道:做取余运算时,c是a/b向0取整之后的结果,我们可以考虑如果不取整,做浮点型计算时a/b的值为t,而此时 a - t * b = 0 ①式,由于t与c都是小于0的,所以c向0取整之后大于t,所以两者乘以一个负数b之后,t * b >= c * b ②式, 由①②两式可得出:a - c * b >= 0 ;也就是说:当被除数大于0,除数小于0时,取余结果c与被除数a同号,同时取模结果与被除数异号。
同理可证:当被除数小于0而除数大于0时,取余结果与被除数同号,取模结果被除数异号。
这与开始时通过少量样例观察出的规律并不冲突,这大大增强了我们观察出的规律的正确性。
结论
在C/C++中 %运算符被定义为取余运算符,并且没有取模运算的概念,在Java中,%也被定义为取余运算符,取模运算要靠Math.floorMod()方法来实现,而在Python中,%被定义为取模运算符。
因此当被除数与除数符号不同时,并且出现%运算符时,在C/C++、Java中可直接初步判断:取余运算的结果的符号与被除数一直,取模运算结果的符号与除数一致;而在Python中,二者“相反”。