树到处都在用递归。。。真的到处都是递归。。。

二叉树的建立：一个结点一个结点地建立二叉树，也用递归

这段代码建立二叉树，需要用户把树的所有结点的数据按照前序遍历的顺序依次输入，这里假设数据都是一个字符，遇到输入为#就不建立结点

/*按前序输入二叉树中的结点的值（假设结点的值是一个字符）*/
/*把输入序列按照前序遍历顺序依次输入，如果遍历到的结点没有数据，则输入#*/
void CreateBiTree(BiTree * T)//BiTree是struct BiTNode *
{
	ElemType ch;
	scanf("%c", &ch);
	if (ch == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTNode));//输入字符不是#，即有数据，则创建结点
		if (!*T)
			exit(OVERFLOW);//没分配到内存，退出并报错堆溢出（不是栈溢出哦）
		(*T)->data = ch;//生成根结点
		CreateBiTree(&(*T)->lchild);//递归构造左子树
		CreateBiTree(&(*T)->rchild); //递归构造右子树
	}
}

用中序遍历方式实现二叉树建立：

/*按中序输入二叉树中的结点的值（假设结点的值是一个字符）*/
/*把输入序列按照中序遍历顺序依次输入，如果遍历到的结点没有数据，则输入#*/
void CreateBiTree(BiTree * T)//BiTree是struct BiTNode *
{
	ElemType ch;
	CreateBiTree(&(*T)->lchild);//递归构造左子树
	scanf("%c", &ch);
	if (ch == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTNode));//输入字符不是#，即有数据，则创建结点
		if (!*T)
			exit(OVERFLOW);//没分配到内存，退出并报错堆溢出（不是栈溢出哦）
		(*T)->data = ch;//生成根结点
		CreateBiTree(&(*T)->rchild); //递归构造右子树
	}
}

用后序遍历方式实现二叉树建立：

/*按后序输入二叉树中的结点的值（假设结点的值是一个字符）*/
/*把输入序列按照后序遍历顺序依次输入，如果遍历到的结点没有数据，则输入#*/
void CreateBiTree(BiTree * T)//BiTree是struct BiTNode *
{
	ElemType ch;
	CreateBiTree(&(*T)->lchild);//递归构造左子树
	CreateBiTree(&(*T)->rchild); //递归构造右子树
	scanf("%c", &ch);
	if (ch == '#')
		*T = NULL;
	else
	{
		*T = (BiTree)malloc(sizeof(BiTNode));//输入字符不是#，即有数据，则创建结点
		if (!*T)
			exit(OVERFLOW);//没分配到内存，退出并报错堆溢出（不是栈溢出哦）
		(*T)->data = ch;//生成根结点
	}
}

线索二叉链表：利用二叉链表的空指针域存储前驱后继信息，但每个结点要多用两个比特内存

线索二叉链表存储结构非常适合于经常遍历结点，或者需要知道结点的前驱后继关系的问题。
他不仅节省了时间，并且也比较省空间哦！这个不容易！！因为他用的空间是二叉链表本来就浪费了的空间。

n个结点的二叉链表有n+1个空指针域

线索，指的是用二叉链表的结点中的空指针域存储的前驱和后继信息（即把二叉树按照某种次序遍历一遍后得到的线性序列的前驱后继关系）。加上线索的二叉链表叫做线索链表，相应二叉树就是线索二叉树Threaded Binary Tree。

之前说过了二叉链表，每个结点有两个指针域，分别指向左孩子和右孩子的结点地址。可以计算一下，有n个结点的二叉树的二叉链表中，一共有2n个指针域，但是只有n-1个非空指针域（除了根节点以外的每个结点都被一个指针指着，所以有n-1个指针域在被使用），于是就有2n-(n-1)=n+1个指针域闲置着没有使用。这是很浪费的，这些空间干嘛不用起来呢？

用这n+1个空指针域存某种遍历次序的前驱后继线索:把二叉链表线索化

于是线索二叉树脑子很灵活，它给这空闲的n+1个指针域安排了一个很有意义的工作：

• 如果一个结点的右孩子指针域如果为空，就让它指向该结点的后继结点（按某种次序遍历得到的线性序列的后继关系）；
• 如果一个结点的左孩子指针域如果为空，就让它指向该结点的前驱结点（按某种次序遍历得到的线性序列的前驱关系）。不是叶子结点，其左孩子指针域也可以是空指针哦，比如右斜树。

经过这两步，所有n+1个空指针域都可以被用起来。

说说为什么用这些空指针域存储这些前驱后继信息是有用的。这是因为：一颗二叉树用二叉链表存储，链表的非空指针域只能存储孩子结点的内存所在位置，但是并不能直接反应遍历时候的前驱后继关系，于是如果想要知道某个结点在遍历时的前驱后继关系，则需要实际做一下遍历才能知道。这很费时间啊。所以如果能存下来这种前驱后继关系岂不是很香？然后二叉链表又刚好空出来n+1个指针域，那干脆用起来咯。以后要知道前驱后继就不需要自己遍历一遍了。

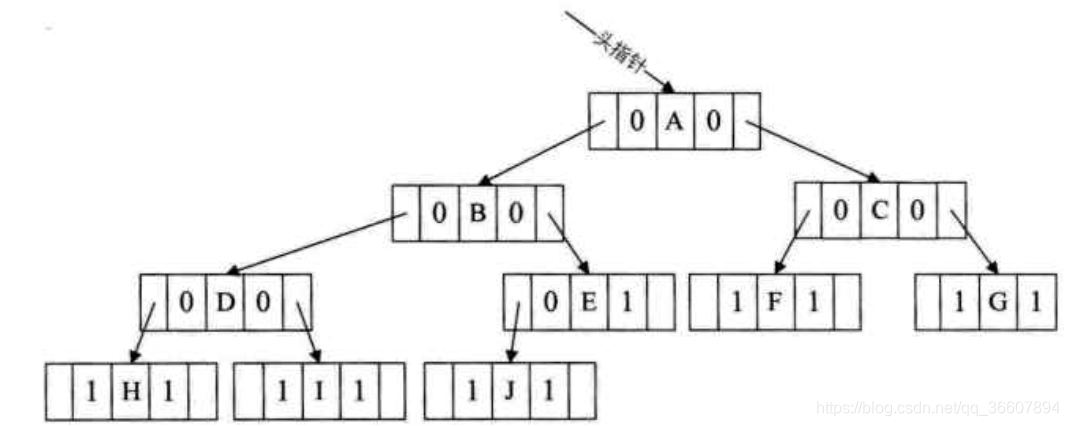
举个例子，假设用了中序遍历，则下图二叉树的中序遍历线性序列是HDIBJEAFCG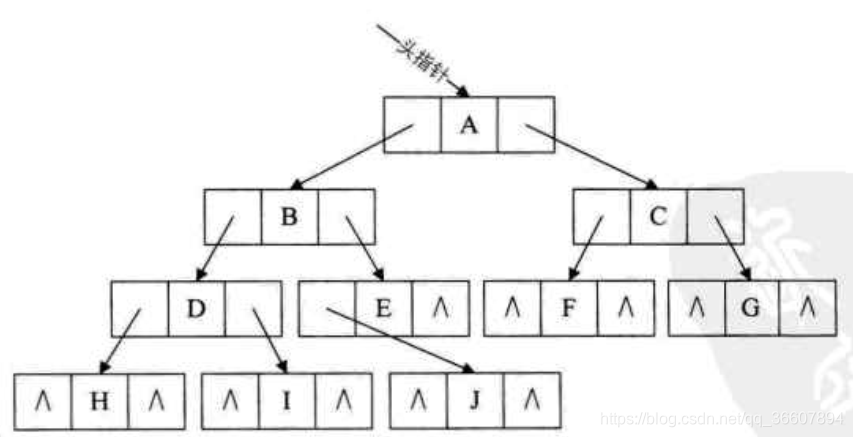

先利用所有空的右孩子指针域,如图，H的右孩子指针域指向其后继结点D，I的右孩子指向B，J···指向E，E···指向A····，写出来：
HD
IB
JE
EA
FC
G NULL

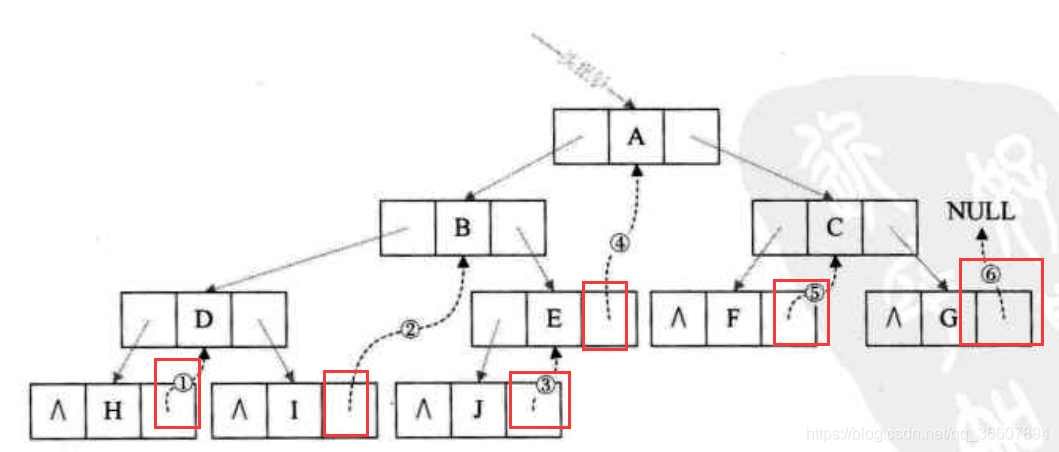
在利用左孩子指针域，如图,H在中序遍历没有前驱，I的前驱是D，J的前驱是B····

NULL H
DI
BJ
AF
CG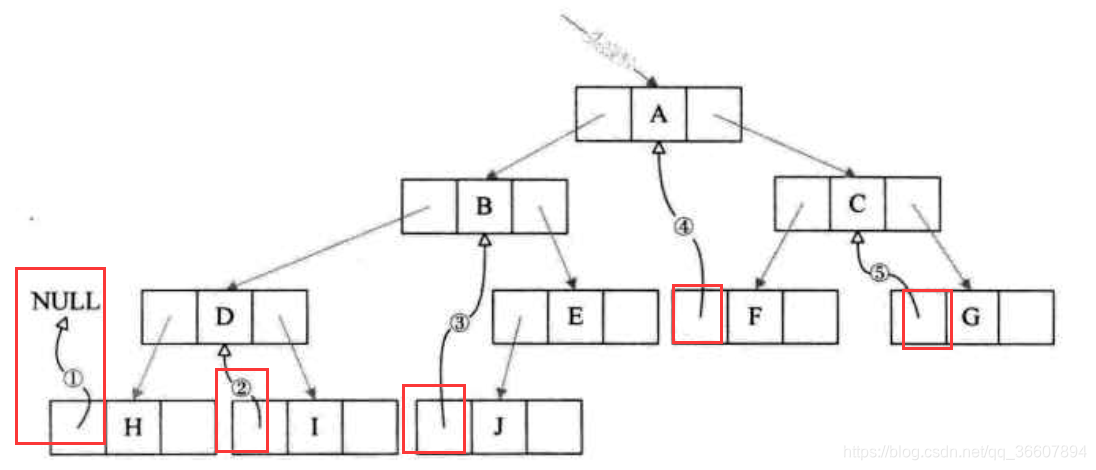

到此为止，这个示例的11个空指针域全部被利用了。根据写出来的11条顺序的组合，就可以得到整个二叉树的中序遍历序列了。

增加2 bit 以明确指针域到底是指向孩子还是指向前驱后继

但是还有一个问题：一个结点怎么知道自己的左孩子指针域是指向了左孩子还是前驱呢？？自己的右孩子指针域是指向了右孩子还是后继呢？
比如E结点的左孩子指针域确实指向了左孩子，而右孩子指针域却指向了后继。

答案是，只能增加标志位。进一步把二叉链表的结点结构设计复杂化：

这才是二叉线索链表的真面目：

好在ltag和rtag是只占1个bit的量，占用内存并没有增多太多。

存为普通二叉链表的样子：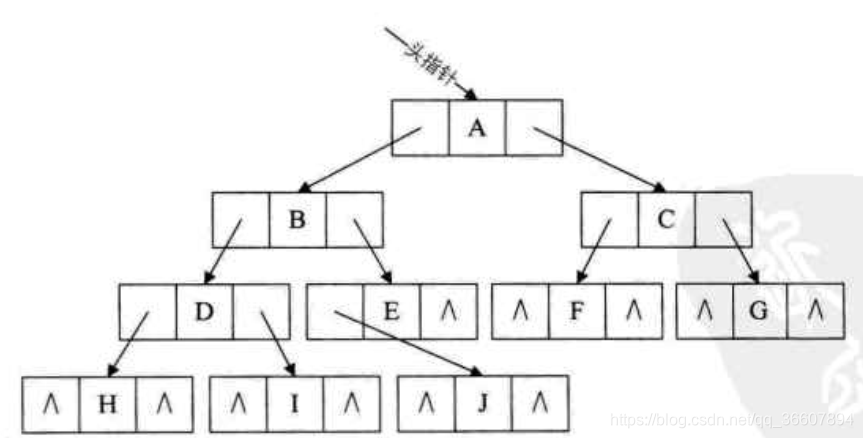

存为二叉线索链表的样子：

代码

二叉线索存储结点的结构

/*二叉树的二叉线索存储结构定义*/
typedef enum{Link, Thread} PointerTag;//Link表示指向孩子；Thread表示指向前驱后继
/*二叉线索存储结点的结构*/
typedef struct BiThrNode
{
	PointerTag LTag;
	PointerTag RTag;
	ElemType data;
	struct BiThrNode * lchild;
	struct BiThrNode * rchild;
}BiThrNode, *BiThrTree;

线索化的实现代码(递归)

因为线索化的本质就是把空指针用来存前驱后继，所以线索化的同时就需要遍历二叉树，因为只有遍历了才能知道前驱后继。

从下面的代码可以看到，线索化就是在遍历这颗二叉树。这里是中序遍历，访问操作是遇到空指针就存储前驱后继信息。

/*中序遍历线索化的递归函数，进行中序遍历的中序线索化*/
BiThrNode * pre = NULL;//前驱，始终指向当前访问结点的前驱结点，即上一个被访问的结点；全局变量，初始化为空指针
void InThreading(BiThrTree p)
{
	if (p)
	{
		InThreading(p->lchild);//递归进行左子树的线索化
		if (!p->lchild)//当前结点没有左孩子
		{
			p->LTag = Thread;//设置标志位
			p->lchild = pre;//存储前驱结点的位置
		}
		if (pre && !pre->rchild)//如果前驱存在且没有右孩子，就把前驱的右孩子存当前结点
		{
			pre->RTag = Thread;
			pre->rchild = p;
		}
		pre = p;//保持pre指向p的前驱
		InThreading(p->rchild);//递归进行右子树的线索化
	}
}

以下图为例，代码首先访问A,然后进入递归，访问B，然后递归访问D，然后再H，进入到H的左子树线索化递归时，由于指向H的左子树的指针p为空，所以直接退出，回退到H的那层递归，判断两个if，由于H确实没有左孩子，所以就把左孩子设置为前驱，即初始化的空指针，第2个if就进不去了。然后pre变为指向H的指针。遍历H的右子树也一下就出来了。回退到D的函数层·······

加个头结点，把线索二叉树链表变为双向链表

没想到这个线索链表这么能玩儿，各种花样玩法，设计者真是脑子好用，羡慕

• 让头结点的左孩子指针域指向根结点（并非中序遍历的第一个访问结点哦），右孩子指针域指向中序遍历访问的最后一个结点；
• 让二叉树中序序列第一个结点的左孩子指针域指向头结点；
• 让二叉树中序序列的最后一个结点的右孩子也指向头结点；

如图：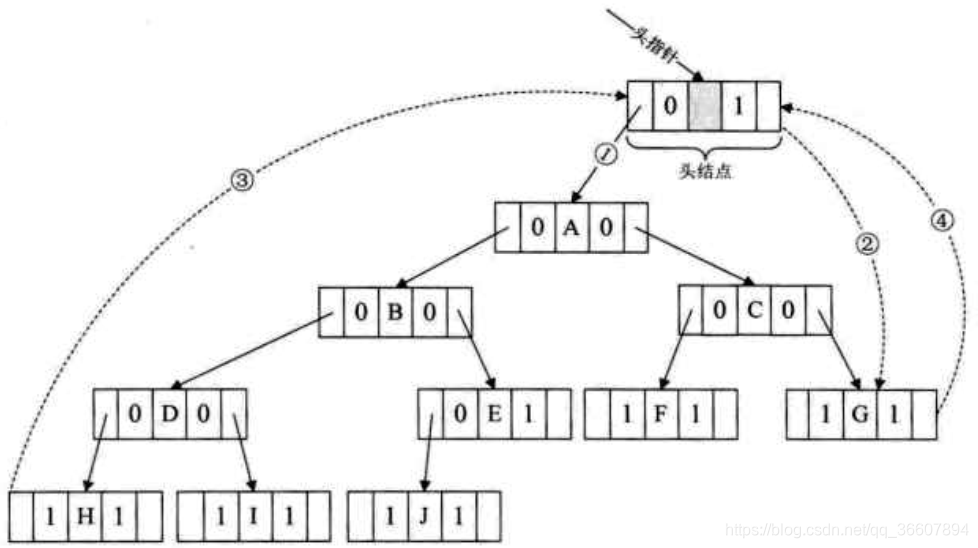

这个代码看了15分钟才看明白，确实是中序遍历的顺序。遍历结点的时候，下一个结点可以是左孩子指针域指向的结点也可以是右孩子指针域指向的结点，即俩方向都可以走，所以像双向链表。

注意这里左孩子可能是前驱，也可能是孩子。右孩子也一样。

/*T指向头结点，二叉树T用二叉线索链表表示*/
//代码的目的是中序遍历二叉线索链表，先访问前驱为头结点的结点（中序序列第一个），最后访问后继为头结点的结点（中序序列最后一个）
Status InOrderTraverse_Thr(BiThrTree T)
{
	BiThrTree p;
	p = T->lchild;//p指向根结点，从根节点出发，但并不是先访问根节点哈
	while (p!=T)//p==T即p指向了头结点，那就说明遍历完毕了，退出
	{
		while (p->LTag == Link)//从根节点一路左下，直到p变为第一个左孩子指针域存前驱的结点
			p = p->lchild;
		printf("%c", p->data);//访问结点的操作，可改为其他
		while (p->RTag == Thread && p->rchild != T)//一直访问后继结点，直到走不动（某结点没有写后继信息）
		{
			p = p->rchild;//p变为当前结点的后继结点
			printf("%c", p->data);//访问这个后继结点
		}
		p = p->rchild;//p变为p的右子树的树根，去访问右子树
	}
}