函数在区间连续可以推出什么_A-22 函数的点连续、单侧连续、区间连续

欢迎光临我的专栏《微积分学习之旅》，一起学习，共同提高。

有些函数在求

时的极限时，可以直接求函数在

时的取值，我们称具有这种特性函数“

在

点连续

”。我们将会看到， 连续性的数学定义与日常用语中的“连续性”的含义有着紧密的联系。（一个连续的过程是逐步地、渐渐发生的，而不会突然中断，或者突然变化。）

函数在某点连续的数学定义

如果
，那么函数
在
点连续。（定义1）

从这个定义可以看出，函数

要在

点连续，暗含着三个要求：

有定义（也就是说，
在函数
的定义域内）；
存在；
。

只有这三个要求同时满足，函数在

处才是连续的。

这个定义保证了函数值在

点附近的取值不会出现“跳跃性”地变化。

物理现象通常是连续的，比如位移和速度随时间的连续变化，这和人的身高变化类似。但是“不连续”也会出现在一些情形之中，比如电流。

从几何图形上，你可以把连续理解为函数在区间上的所有点构成的图像没有间断。

例1 下图是函数

的图像，请问函数在哪些点是不连续的？为什么？

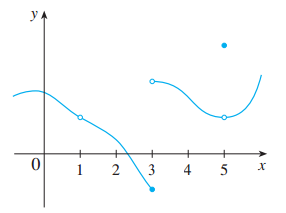
解答：

（1）显而易见，函数

处是不连续的，因为图像在该处有空缺。正经来说，是因为函数

没有定义。

（2）函数同样在

处也是空缺的，导致函数在该处也是不连续的，而这是因为函数在

时的极限不存在（左右极限不相等）。

（3）那么

时的情况怎么样呢？在这里，

既有定义，

也存在，但是

，所以函数

在a=5处也是不连续的。

接下来，让我们看看，当函数是用公式表达的时候，如何判断函数的不连续性。

例2 请判断下列函数在哪些位置不连续。

（a）

;

（b）

;

（c）

;

（d）

解答

（a）注意到

没有定义，所以函数

在2处是不连续的。在后面，我们将会看到为什么

在其它所有点上又是连续的。

（b）注意到

有定义，但是极限

不存在，所以函数

在0处是不连续的。

（c）注意到

有定义，并且极限

，

但是

，所以函数

在2处也是不连续的。

（d）取整函数

在所有的整数位置都是不连续的。因为在

取整数时，极限

不存在。

以上函数如下图所示。

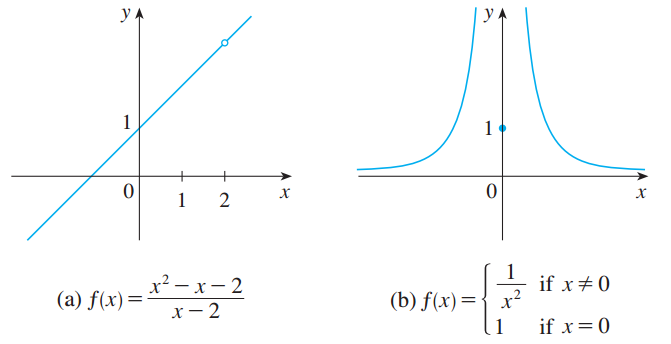
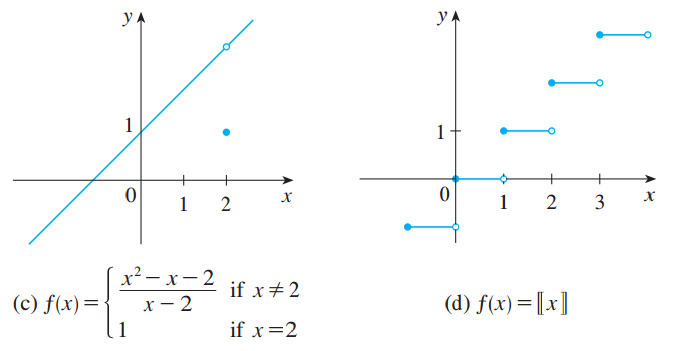
函数单侧连续的定义

如果
，那么函数
在
点右侧连续；

如果
，那么函数
在
点左侧连续。
（定义2）

例3 ，对每一个整数

, 取整函数

都是右侧连续，但是左侧不连续。因为

则在

处右连续，但是

则在

处左侧不连续。

函数在区间上连续的定义

如果函数
在定义域的某个区间上的每一个点都连续，那么函数在这个区间上连续。（如果函数
在区间的左（右）端点有定义，而在右（左）端点没有定义，我们把这个连续性理解为自端点右（左）侧连续。）
（定义3）

例题4 证明函数

在区间

上连续。

解答令

，根据极限法则，我们有

因此，根据定义1，当

时，函数

在

点连续。类似的计算告诉我们

所以函数

在-1的右侧连续，且在1的左侧连续。再根据定义3可知，函数在区间

上连续。

下图是函数

的图像，它是圆

的下半部分。

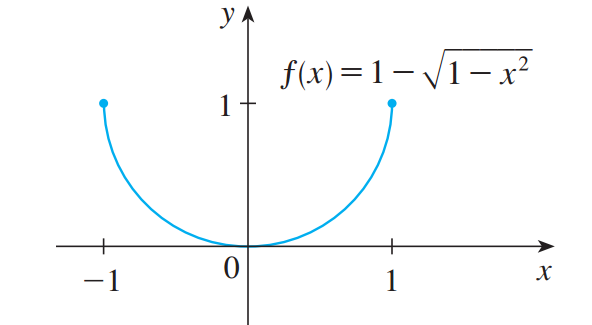
与其利用上述三个定义来验证函数的连续性，就像例题4这样，我们倒不如采用一些更方便的做法，利用简单的连续函数构造更为复杂的连续函数。我们下回再见。

本专栏最新目录请参阅：

专栏目录-《微积分学习之旅》zhuanlan.zhihu.com

（如果您喜欢本专栏，请点击关注；如果认可我的笔记，也请点个赞同呗）

原文链接：https://blog.csdn.net/weixin_29388659/article/details/112068593