欧拉公式是什么？

一、数系

  1. 自然数：1,2,3，……（对于减法不封闭）
  2. 整数Z：……，-1,0,1，……（除法不封闭）
  3. 有理数Q：{{x|x=p/q, p,q\in \mathbb{Z}}}（开方不封闭）根号2；
  4. 实数R：与数轴上的点一一对应；

二、复数

  1. 虚数：i；
  2. 复数a+bi：

 

在这一数学基础上，人们知道了一个数的实数次幂是多少，那么问题来了！一个数的复数次幂是多少呢？？

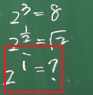
因此，为了研究一个数的复数次幂等于多少，欧拉提出了一个公式，即欧拉公式。

三、欧拉公式

  • 欧拉公式：e^{i\theta }=cos\theta +isin\theta

 这就告诉了我们 一个数的复数次幂是多少。

 

  • 欧拉恒等式：

当θ=π时，有e^{i\pi }+1=0;

欧拉恒等式也被称为“最美恒等式”。

四、欧拉公式的证明

泰勒展开证明

微分方程证明

版权声明：本文为weixin_38121168原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接和本声明。