行列式

行列式是线性代数的一个重要组成部分.它是研究矩阵、线性方程组、特征多项式的重要工具.本章介绍了行列式的定义、性质及计算方法，最后给出了它的两个应用—秩和克莱姆法则.

给定矩阵A，从中选择顶若干行和若干列，将其余的行和列都删去，剩下的元素按原来的排列顺序排成一个矩阵叫做A的子矩阵。
在n阶方阵中，把元素a_ij所在的第i行和第j列划去，留下来的n-1阶矩阵叫做a_ij的与子矩阵，记作M_ij。

M_ij:余子矩阵
|M_ij|:余子式
（-1）^i+j|M_ij|:代数余子式
定义：行列式的值等于他的第一行的个元素与其对应的代数余子式乘积之和，即
detA=A=a₁₁A₁₁+a₁₂A₁₂+…+a_1nA_1n=${\sum }_{j=1}^n{a}_{1j}{A}_{1j}$

二阶行列式的计算——对角线法则

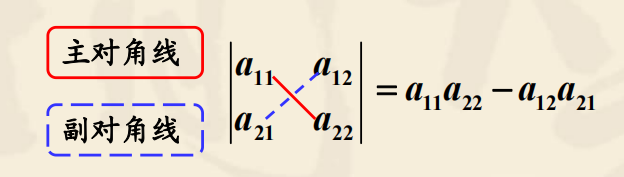
即：主对角线上两元素之积——副对角线上两元素之积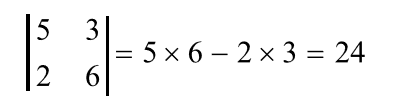

特殊矩阵的行列式

2.2 n阶行列式的性质

性质1 行列式等于它的任一行（列）的各元素与其对应的代数余子式乘积之和，即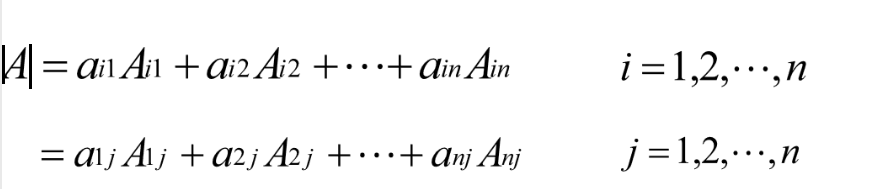

性质2 行列式与它的转置行列式相等。

矩阵的初等变换对行列式的影响

第一种初等变换对行列式的影响：
呼唤行列式的两行（列），行列式添加一个负号。
第二种初等变换对行列式的影响：
行列式的某一行（列）中所有的元素都成一同一个背书，等于此倍数乘以此行列式。
第三种初等变换对行列式的影响：
吧行列式的某一列（行）的个元素乘以同一个倍数后加到另一列（行）对应的元素上去，行列式不变。


和的性质 若行列式 某一行(列)的所有元素都是两个数的和,则此行列式等于两个行列式的和. 这两个行列式的这一行(列)的元素分别为对应的两个加数之一，其余各行(列)的元素与原行列式相同 .


例 计算n阶行列式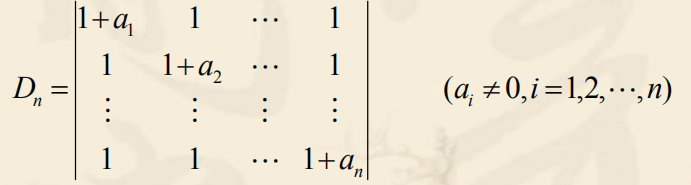


例 计算n阶行列式

注意到行列式各行元素之和等于$x+{\sum }_{i=1}^n{a}_i$，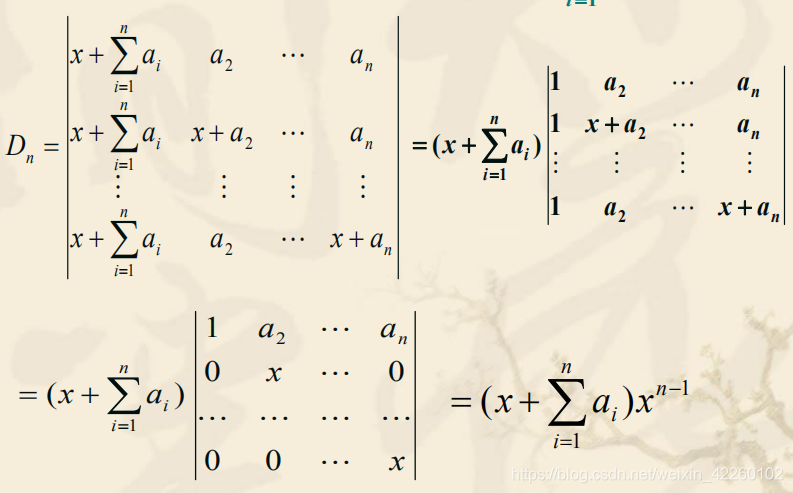

例 范德蒙行列式

补充：有关代数余子式的计算
定理：行列式任一行（列）的元素与另一行（列）的对应元素的代数余子式乘积之和等于零，即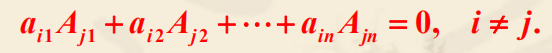

3 行列式的一个应用

矩阵的秩
矩阵 A 的秩定义为 A 中最高阶非零子式的阶数．

1. 若矩阵A中有某个s阶子式不等于零，则 R(A)≥s ；
   若矩阵A中所有s +1阶子式等于零，则R(A)≤s .
2. 若A为 m×n 矩阵，则0≤R(A)≤min(m, n) ．
3. R(AT) = R(A) ．

定理：提醒矩阵的非零行数为秩。
定理：若A~B，则R（A） ~ R（B）。
求矩阵秩的方法：用初等变换化矩阵为梯形矩阵则该梯形矩阵非零行的个数即为矩阵的秩.

克拉默法则

那么线性方程组（1）有解并且解释唯一的，解可以表示成：
$x_1=\frac{D1}{D},x_2=\frac{D2}{D},...,x_n=\frac{Dn}{D}$
其中Dj是把系数行列式D中第j列的元素用方程组有段的常数项代替后所得到的n阶行列式，即