0-1背包
考虑一个背包问题,共有n=5个物品,背包容量为W=10,物品的重量和价值分别为:w={2,2,6,5,4},v={6,3,5,4,6},求背包问题的最大装包价值。若此为0-1背包问题,分析该问题具有最优子结构,其中c(i,j)表示i个物品、容量为j的0-1背包问题的最大装包价值,最终要求解c(n,W)。 采用自底向上的动态规划方法求解,得到最大装包价值为(62)
| W | V | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 6 | 0 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 | 6 |
| 2 | 3 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 9 | 9 | 9 |
| 6 | 5 | 0 | 6 | 6 | 9 | 9 | 9 | 9 | 11 | 11 | 11 |
| 5 | 4 | 0 | 6 | 6 | 6 | 9 | 9 | 10 | 11 | 13 | 13 |
| 4 | 6 | 0 | 6 | 6 | 6 | 9 | 12 | 12 | 12 | 15 | 15 |
0-1背包问题是指每一种物品都只有一件,如果容量够的话,可以选择放或者不放,不放或容量不够的情况下就把上一个物品的价格拿下来;放的话就是当前容量减去所需容量得到序号为上一个物品对应的容量+当前容量跟上一个相同的序号容量进行对比,取最大
(1)假如我们放进背包,f[i][j] = f[i - 1][j - weight[i]] + value[i],这里的f[i - 1][j - weight[i]] + value[i]应该这么理解:在没放这件物品之前的状态值加上要放进去这件物品的价值。而对于f[i - 1][j - weight[i]]这部分,i - 1很容易理解,关键是 j - weight[i]这里,我们要明白:要把这件物品放进背包,就得在背包里面预留这一部分空间。
(2)假如我们不放进背包,f[i][j] = f[i - 1][j],这个很容易理解
多重背包
| 编号 | 个数 | W | V | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 2 | 2 | 6 | 0 | ||||
| 2 | 3 | 2 | 3 | 0 | ||||
| 3 | 4 | 6 | 5 | 0 | ||||
| 4 | 2 | 5 | 4 | 0 | ||||
| 5 | 1 | 4 | 6 | 0 |
转化为0-1背包 朴素方法 时间复杂度![]()
| 编号 | 个数 | W | V | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 2 | 6 | 0 | ||||
| 1 | 1 | 2 | 6 | 0 | ||||
| 2 | 1 | 2 | 3 | 0 | ||||
| 2 | 1 | 2 | 3 | 0 | ||||
| 2 | 1 | 2 | 3 | 0 | ||||
| 3 | 1 | 6 | 5 | 0 | ||||
| 3 | 1 | 6 | 5 | 0 | ||||
| 3 | 1 | 6 | 5 | 0 | ||||
| 3 | 1 | 6 | 5 | 0 | ||||
| 4 | 1 | 5 | 4 | 0 | ||||
| 4 | 1 | 5 | 4 | 0 | ||||
| 5 | 1 | 4 | 6 | 0 |
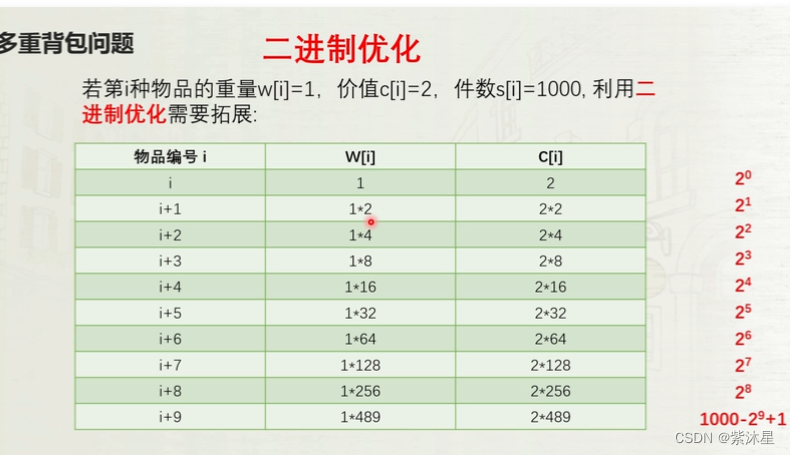
二进制:
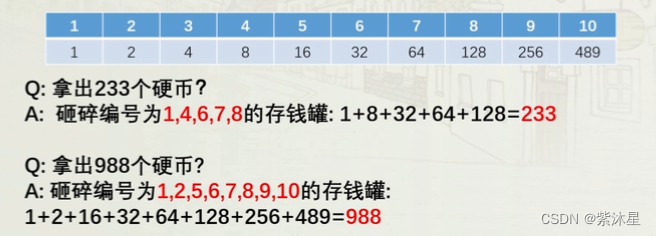
1-511可直接取值
512-1000为减490,然后值取二进制
完全背包
=1时,计算只放第一件物品的最大价值。
i=2时,计算加上第二件物品的最大价值(在只放第一件物品的前提下)
以此类推……
值得注意的是,第二层循环要从j=weight[i]开始,这个稍微理解一下即可
放的话就是当前容量减去所需容量得到序号为当前物品对应的容量+当前容量跟上一个相同的序号容量进行对比,取最大
